WildIng: A Wildlife Image Invariant Representation Model for Geographical Domain Shift

Wildlife monitoring is crucial for studying biodiversity loss and climate change. Camera trap images provide a non-intrusive method for analyzing animal populations and identifying ecological patterns over time. However, manual analysis is time-consuming and resource-intensive. Deep learning, particularly foundation models, has been applied to automate wildlife identification, achieving strong performance when tested on data from the same geographical locations as their training sets. Yet, despite their promise, these models struggle to generalize to new geographical areas, leading to significant performance drops. For example, training an advanced vision-language model, such as CLIP with an adapter, on an African dataset achieves an accuracy of 84.77%. However, this performance drops significantly to 16.17% when the model is tested on an American dataset. This limitation partly arises because existing models rely predominantly on image-based representations, making them sensitive to geographical data distribution shifts, such as variation in background, lighting, and environmental conditions. To address this, we introduce WildIng, a Wildlife image Invariant representation model for geographical domain shift. WildIng integrates text descriptions with image features, creating a more robust representation to geographical domain shifts. By leveraging textual descriptions, our approach captures consistent semantic information, such as detailed descriptions of the appearance of the species, improving generalization across different geographical locations. Experiments show that WildIng enhances the accuracy of foundation models such as BioCLIP by 30% under geographical domain shift conditions. We evaluate WildIng on two datasets collected from different regions, namely America and Africa. The code and models are publicly available at https://github.com/Julian075/CATALOG/tree/WildIng.

Subgraph Gaussian Embedding Contrast for Self-Supervised Graph Representation Learning

Graph Representation Learning (GRL) is a fundamental task in machine learning, aiming to encode high-dimensional graph-structured data into low-dimensional vectors. Self-Supervised Learning (SSL) methods are widely used in GRL because they can avoid expensive human annotation. In this work, we propose a novel Subgraph Gaussian Embedding Contrast (SubGEC) method. Our approach introduces a subgraph Gaussian embedding module, which adaptively maps subgraphs to a structured Gaussian space, ensuring the preservation of input subgraph characteristics while generating subgraphs with a controlled distribution. We then employ optimal transport distances, more precisely the Wasserstein and Gromov-Wasserstein distances, to effectively measure the similarity between subgraphs, enhancing the robustness of the contrastive learning process. Extensive experiments across multiple benchmarks demonstrate that \method~outperforms or presents competitive performance against state-of-the-art approaches. Our findings provide insights into the design of SSL methods for GRL, emphasizing the importance of the distribution of the generated contrastive pairs.

Piecewise Constant Spectral Graph Neural Network

Graph Neural Networks (GNNs) have achieved significant success across various domains by leveraging graph structures in data. Existing spectral GNNs, which use low-degree polynomial filters to capture graph spectral properties, may not fully identify the graph's spectral characteristics because of the polynomial's small degree. However, increasing the polynomial degree is computationally expensive and beyond certain thresholds leads to performance plateaus or degradation. In this paper, we introduce the Piecewise Constant Spectral Graph Neural Network(PieCoN) to address these challenges. PieCoN combines constant spectral filters with polynomial filters to provide a more flexible way to leverage the graph structure. By adaptively partitioning the spectrum into intervals, our approach increases the range of spectral properties that can be effectively learned. Experiments on nine benchmark datasets, including both homophilic and heterophilic graphs, demonstrate that PieCoN is particularly effective on heterophilic datasets, highlighting its potential for a wide range of applications.

COSMOS: Continuous Simplicial Neural Networks

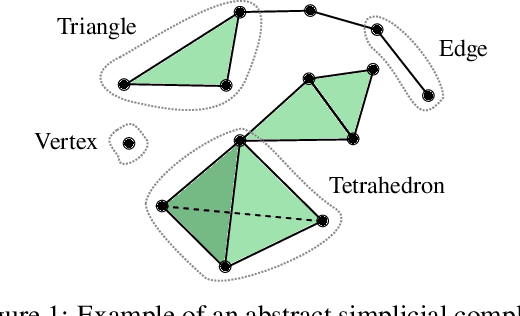
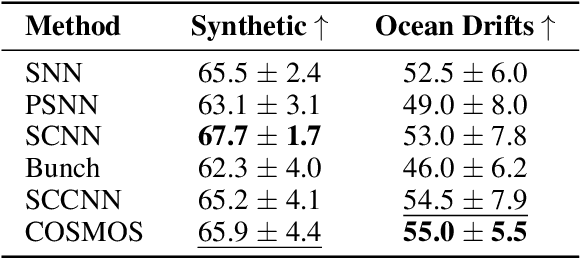
Simplicial complexes provide a powerful framework for modeling high-order interactions in structured data, making them particularly suitable for applications such as trajectory prediction and mesh processing. However, existing simplicial neural networks (SNNs), whether convolutional or attention-based, rely primarily on discrete filtering techniques, which can be restrictive. In contrast, partial differential equations (PDEs) on simplicial complexes offer a principled approach to capture continuous dynamics in such structures. In this work, we introduce COntinuous SiMplicial neural netwOrkS (COSMOS), a novel SNN architecture derived from PDEs on simplicial complexes. We provide theoretical and experimental justifications of COSMOS's stability under simplicial perturbations. Furthermore, we investigate the over-smoothing phenomenon, a common issue in geometric deep learning, demonstrating that COSMOS offers better control over this effect than discrete SNNs. Our experiments on real-world datasets of ocean trajectory prediction and regression on partial deformable shapes demonstrate that COSMOS achieves competitive performance compared to state-of-the-art SNNs in complex and noisy environments.

A Fused Gromov-Wasserstein Approach to Subgraph Contrastive Learning

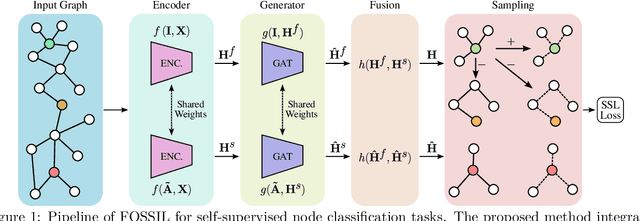
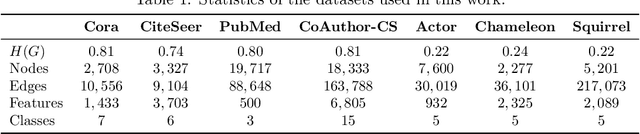
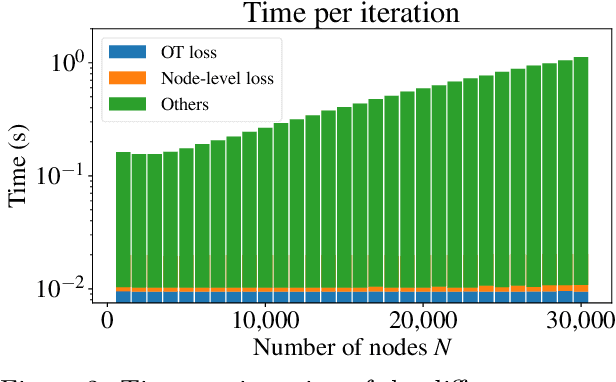
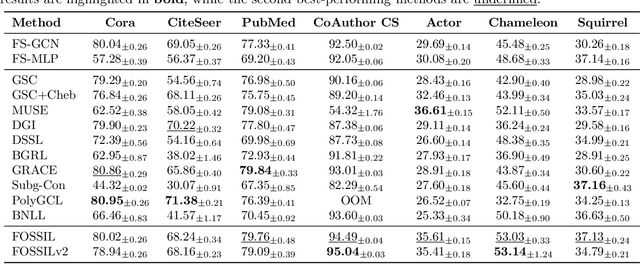
Self-supervised learning has become a key method for training deep learning models when labeled data is scarce or unavailable. While graph machine learning holds great promise across various domains, the design of effective pretext tasks for self-supervised graph representation learning remains challenging. Contrastive learning, a popular approach in graph self-supervised learning, leverages positive and negative pairs to compute a contrastive loss function. However, current graph contrastive learning methods often struggle to fully use structural patterns and node similarities. To address these issues, we present a new method called Fused Gromov Wasserstein Subgraph Contrastive Learning (FOSSIL). Our model integrates node-level and subgraph-level contrastive learning, seamlessly combining a standard node-level contrastive loss with the Fused Gromov-Wasserstein distance. This combination helps our method capture both node features and graph structure together. Importantly, our approach works well with both homophilic and heterophilic graphs and can dynamically create views for generating positive and negative pairs. Through extensive experiments on benchmark graph datasets, we show that FOSSIL outperforms or achieves competitive performance compared to current state-of-the-art methods.

CATALOG: A Camera Trap Language-guided Contrastive Learning Model

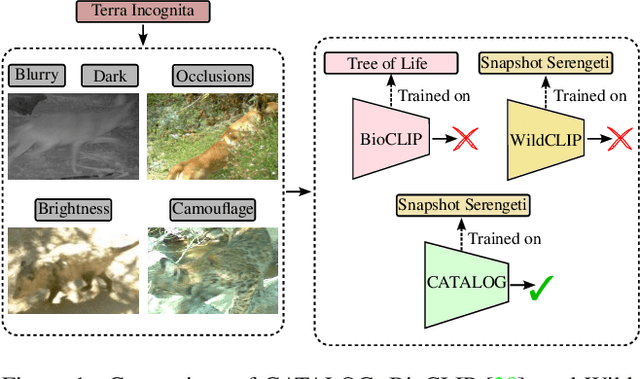
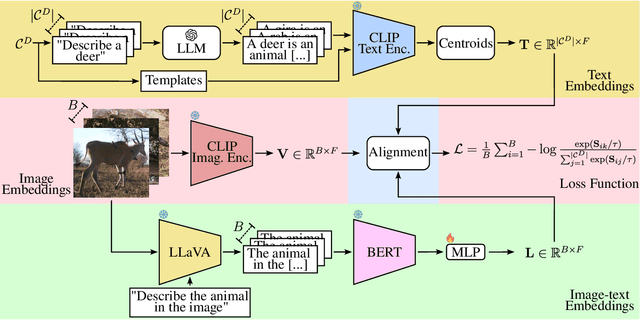
Foundation Models (FMs) have been successful in various computer vision tasks like image classification, object detection and image segmentation. However, these tasks remain challenging when these models are tested on datasets with different distributions from the training dataset, a problem known as domain shift. This is especially problematic for recognizing animal species in camera-trap images where we have variability in factors like lighting, camouflage and occlusions. In this paper, we propose the Camera Trap Language-guided Contrastive Learning (CATALOG) model to address these issues. Our approach combines multiple FMs to extract visual and textual features from camera-trap data and uses a contrastive loss function to train the model. We evaluate CATALOG on two benchmark datasets and show that it outperforms previous state-of-the-art methods in camera-trap image recognition, especially when the training and testing data have different animal species or come from different geographical areas. Our approach demonstrates the potential of using FMs in combination with multi-modal fusion and contrastive learning for addressing domain shifts in camera-trap image recognition. The code of CATALOG is publicly available at https://github.com/Julian075/CATALOG.

Variational Graph Contrastive Learning

Graph representation learning (GRL) is a fundamental task in machine learning, aiming to encode high-dimensional graph-structured data into low-dimensional vectors. Self-supervised learning (SSL) methods are widely used in GRL because they can avoid expensive human annotation. In this work, we propose a novel Subgraph Gaussian Embedding Contrast (SGEC) method. Our approach introduces a subgraph Gaussian embedding module, which adaptively maps subgraphs to a structured Gaussian space, ensuring the preservation of graph characteristics while controlling the distribution of generated subgraphs. We employ optimal transport distances, including Wasserstein and Gromov-Wasserstein distances, to effectively measure the similarity between subgraphs, enhancing the robustness of the contrastive learning process. Extensive experiments across multiple benchmarks demonstrate that SGEC outperforms or presents competitive performance against state-of-the-art approaches. Our findings provide insights into the design of SSL methods for GRL, emphasizing the importance of the distribution of the generated contrastive pairs.

Higher-Order GNNs Meet Efficiency: Sparse Sobolev Graph Neural Networks

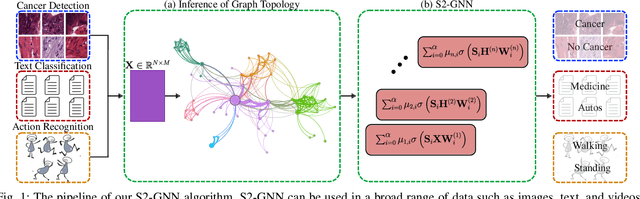
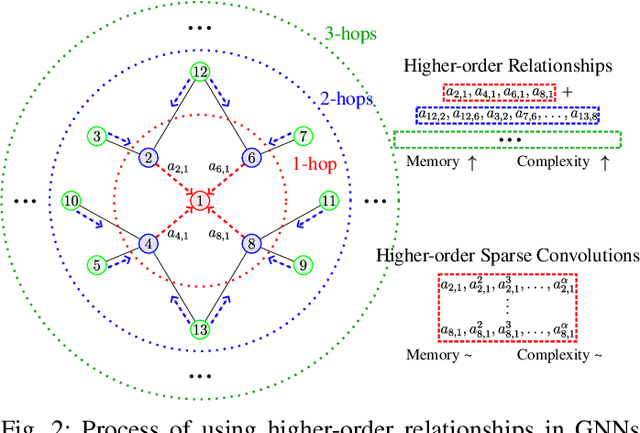
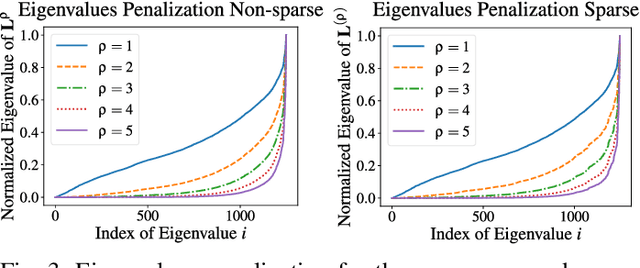
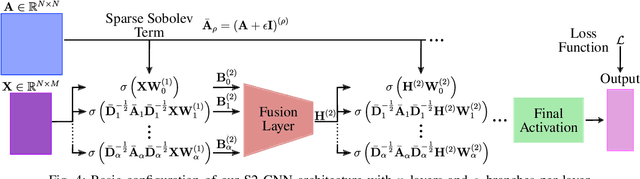
Graph Neural Networks (GNNs) have shown great promise in modeling relationships between nodes in a graph, but capturing higher-order relationships remains a challenge for large-scale networks. Previous studies have primarily attempted to utilize the information from higher-order neighbors in the graph, involving the incorporation of powers of the shift operator, such as the graph Laplacian or adjacency matrix. This approach comes with a trade-off in terms of increased computational and memory demands. Relying on graph spectral theory, we make a fundamental observation: the regular and the Hadamard power of the Laplacian matrix behave similarly in the spectrum. This observation has significant implications for capturing higher-order information in GNNs for various tasks such as node classification and semi-supervised learning. Consequently, we propose a novel graph convolutional operator based on the sparse Sobolev norm of graph signals. Our approach, known as Sparse Sobolev GNN (S2-GNN), employs Hadamard products between matrices to maintain the sparsity level in graph representations. S2-GNN utilizes a cascade of filters with increasing Hadamard powers to generate a diverse set of functions. We theoretically analyze the stability of S2-GNN to show the robustness of the model against possible graph perturbations. We also conduct a comprehensive evaluation of S2-GNN across various graph mining, semi-supervised node classification, and computer vision tasks. In particular use cases, our algorithm demonstrates competitive performance compared to state-of-the-art GNNs in terms of performance and running time.

GABIC: Graph-based Attention Block for Image Compression

While standardized codecs like JPEG and HEVC-intra represent the industry standard in image compression, neural Learned Image Compression (LIC) codecs represent a promising alternative. In detail, integrating attention mechanisms from Vision Transformers into LIC models has shown improved compression efficiency. However, extra efficiency often comes at the cost of aggregating redundant features. This work proposes a Graph-based Attention Block for Image Compression (GABIC), a method to reduce feature redundancy based on a k-Nearest Neighbors enhanced attention mechanism. Our experiments show that GABIC outperforms comparable methods, particularly at high bit rates, enhancing compression performance.

WiGNet: Windowed Vision Graph Neural Network

In recent years, Graph Neural Networks (GNNs) have demonstrated strong adaptability to various real-world challenges, with architectures such as Vision GNN (ViG) achieving state-of-the-art performance in several computer vision tasks. However, their practical applicability is hindered by the computational complexity of constructing the graph, which scales quadratically with the image size. In this paper, we introduce a novel Windowed vision Graph neural Network (WiGNet) model for efficient image processing. WiGNet explores a different strategy from previous works by partitioning the image into windows and constructing a graph within each window. Therefore, our model uses graph convolutions instead of the typical 2D convolution or self-attention mechanism. WiGNet effectively manages computational and memory complexity for large image sizes. We evaluate our method in the ImageNet-1k benchmark dataset and test the adaptability of WiGNet using the CelebA-HQ dataset as a downstream task with higher-resolution images. In both of these scenarios, our method achieves competitive results compared to previous vision GNNs while keeping memory and computational complexity at bay. WiGNet offers a promising solution toward the deployment of vision GNNs in real-world applications. We publicly released the code at https://github.com/EIDOSLAB/WiGNet.