Aref Einizade
Subgraph Gaussian Embedding Contrast for Self-Supervised Graph Representation Learning
May 29, 2025Abstract:Graph Representation Learning (GRL) is a fundamental task in machine learning, aiming to encode high-dimensional graph-structured data into low-dimensional vectors. Self-Supervised Learning (SSL) methods are widely used in GRL because they can avoid expensive human annotation. In this work, we propose a novel Subgraph Gaussian Embedding Contrast (SubGEC) method. Our approach introduces a subgraph Gaussian embedding module, which adaptively maps subgraphs to a structured Gaussian space, ensuring the preservation of input subgraph characteristics while generating subgraphs with a controlled distribution. We then employ optimal transport distances, more precisely the Wasserstein and Gromov-Wasserstein distances, to effectively measure the similarity between subgraphs, enhancing the robustness of the contrastive learning process. Extensive experiments across multiple benchmarks demonstrate that \method~outperforms or presents competitive performance against state-of-the-art approaches. Our findings provide insights into the design of SSL methods for GRL, emphasizing the importance of the distribution of the generated contrastive pairs.
COSMOS: Continuous Simplicial Neural Networks
Mar 17, 2025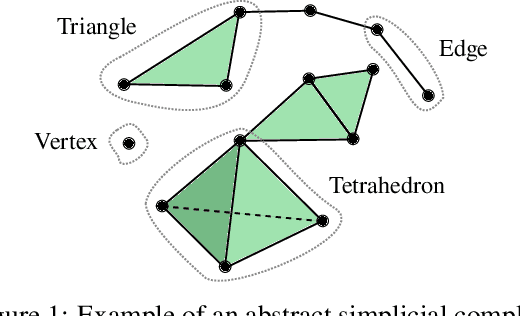
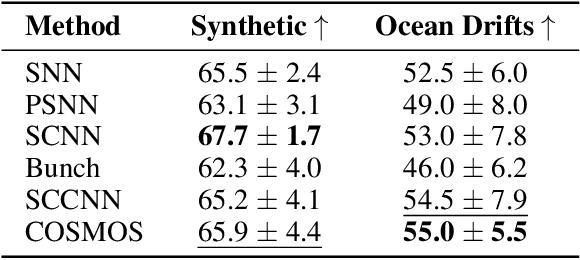


Abstract:Simplicial complexes provide a powerful framework for modeling high-order interactions in structured data, making them particularly suitable for applications such as trajectory prediction and mesh processing. However, existing simplicial neural networks (SNNs), whether convolutional or attention-based, rely primarily on discrete filtering techniques, which can be restrictive. In contrast, partial differential equations (PDEs) on simplicial complexes offer a principled approach to capture continuous dynamics in such structures. In this work, we introduce COntinuous SiMplicial neural netwOrkS (COSMOS), a novel SNN architecture derived from PDEs on simplicial complexes. We provide theoretical and experimental justifications of COSMOS's stability under simplicial perturbations. Furthermore, we investigate the over-smoothing phenomenon, a common issue in geometric deep learning, demonstrating that COSMOS offers better control over this effect than discrete SNNs. Our experiments on real-world datasets of ocean trajectory prediction and regression on partial deformable shapes demonstrate that COSMOS achieves competitive performance compared to state-of-the-art SNNs in complex and noisy environments.
Higher-Order GNNs Meet Efficiency: Sparse Sobolev Graph Neural Networks
Nov 07, 2024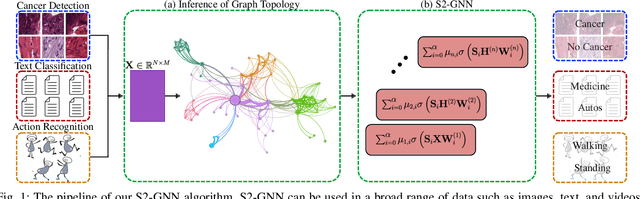
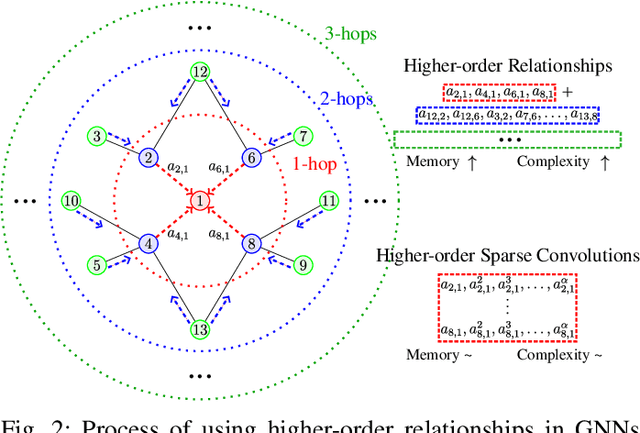
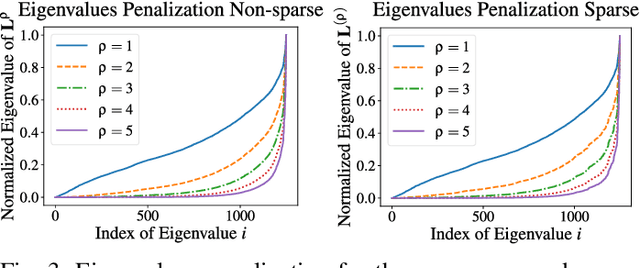
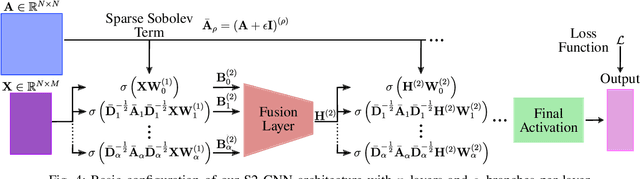
Abstract:Graph Neural Networks (GNNs) have shown great promise in modeling relationships between nodes in a graph, but capturing higher-order relationships remains a challenge for large-scale networks. Previous studies have primarily attempted to utilize the information from higher-order neighbors in the graph, involving the incorporation of powers of the shift operator, such as the graph Laplacian or adjacency matrix. This approach comes with a trade-off in terms of increased computational and memory demands. Relying on graph spectral theory, we make a fundamental observation: the regular and the Hadamard power of the Laplacian matrix behave similarly in the spectrum. This observation has significant implications for capturing higher-order information in GNNs for various tasks such as node classification and semi-supervised learning. Consequently, we propose a novel graph convolutional operator based on the sparse Sobolev norm of graph signals. Our approach, known as Sparse Sobolev GNN (S2-GNN), employs Hadamard products between matrices to maintain the sparsity level in graph representations. S2-GNN utilizes a cascade of filters with increasing Hadamard powers to generate a diverse set of functions. We theoretically analyze the stability of S2-GNN to show the robustness of the model against possible graph perturbations. We also conduct a comprehensive evaluation of S2-GNN across various graph mining, semi-supervised node classification, and computer vision tasks. In particular use cases, our algorithm demonstrates competitive performance compared to state-of-the-art GNNs in terms of performance and running time.
Spatiotemporal Forecasting Meets Efficiency: Causal Graph Process Neural Networks
May 29, 2024Abstract:Graph Neural Networks (GNNs) have advanced spatiotemporal forecasting by leveraging relational inductive biases among sensors (or any other measuring scheme) represented as nodes in a graph. However, current methods often rely on Recurrent Neural Networks (RNNs), leading to increased runtimes and memory use. Moreover, these methods typically operate within 1-hop neighborhoods, exacerbating the reduction of the receptive field. Causal Graph Processes (CGPs) offer an alternative, using graph filters instead of MLP layers to reduce parameters and minimize memory consumption. This paper introduces the Causal Graph Process Neural Network (CGProNet), a non-linear model combining CGPs and GNNs for spatiotemporal forecasting. CGProNet employs higher-order graph filters, optimizing the model with fewer parameters, reducing memory usage, and improving runtime efficiency. We present a comprehensive theoretical and experimental stability analysis, highlighting key aspects of CGProNet. Experiments on synthetic and real data demonstrate CGProNet's superior efficiency, minimizing memory and time requirements while maintaining competitive forecasting performance.
Continuous Product Graph Neural Networks
May 29, 2024



Abstract:Processing multidomain data defined on multiple graphs holds significant potential in various practical applications in computer science. However, current methods are mostly limited to discrete graph filtering operations. Tensorial partial differential equations on graphs (TPDEGs) provide a principled framework for modeling structured data across multiple interacting graphs, addressing the limitations of the existing discrete methodologies. In this paper, we introduce Continuous Product Graph Neural Networks (CITRUS) that emerge as a natural solution to the TPDEG. CITRUS leverages the separability of continuous heat kernels from Cartesian graph products to efficiently implement graph spectral decomposition. We conduct thorough theoretical analyses of the stability and over-smoothing properties of CITRUS in response to domain-specific graph perturbations and graph spectra effects on the performance. We evaluate CITRUS on well-known traffic and weather spatiotemporal forecasting datasets, demonstrating superior performance over existing approaches.
Kernel-based Joint Multiple Graph Learning and Clustering of Graph Signals
Nov 07, 2023Abstract:Within the context of Graph Signal Processing (GSP), Graph Learning (GL) is concerned with the inference of the graph's underlying structure from nodal observations. However, real-world data often contains diverse information, necessitating the simultaneous clustering and learning of multiple graphs. In practical applications, valuable node-specific covariates, represented as kernels, have been underutilized by existing graph signal clustering methods. In this letter, we propose a new framework, named Kernel-based joint Multiple GL and clustering of graph signals (KMGL), that leverages a multi-convex optimization approach. This allows us to integrate node-side information, construct low-pass filters, and efficiently solve the optimization problem. The experiments demonstrate that KMGL significantly enhances the robustness of GL and clustering, particularly in scenarios with high noise levels and a substantial number of clusters. These findings underscore the potential of KMGL for improving the performance of GSP methods in diverse, real-world applications.
ProductGraphSleepNet: Sleep Staging using Product Spatio-Temporal Graph Learning with Attentive Temporal Aggregation
Dec 09, 2022



Abstract:The classification of sleep stages plays a crucial role in understanding and diagnosing sleep pathophysiology. Sleep stage scoring relies heavily on visual inspection by an expert that is time consuming and subjective procedure. Recently, deep learning neural network approaches have been leveraged to develop a generalized automated sleep staging and account for shifts in distributions that may be caused by inherent inter/intra-subject variability, heterogeneity across datasets, and different recording environments. However, these networks ignore the connections among brain regions, and disregard the sequential connections between temporally adjacent sleep epochs. To address these issues, this work proposes an adaptive product graph learning-based graph convolutional network, named ProductGraphSleepNet, for learning joint spatio-temporal graphs along with a bidirectional gated recurrent unit and a modified graph attention network to capture the attentive dynamics of sleep stage transitions. Evaluation on two public databases: the Montreal Archive of Sleep Studies (MASS) SS3; and the SleepEDF, which contain full night polysomnography recordings of 62 and 20 healthy subjects, respectively, demonstrates performance comparable to the state-of-the-art (Accuracy: 0.867;0.838, F1-score: 0.818;0.774 and Kappa: 0.802;0.775, on each database respectively). More importantly, the proposed network makes it possible for clinicians to comprehend and interpret the learned connectivity graphs for sleep stages.
Estimation of a Causal Directed Acyclic Graph Process using Non-Gaussianity
Nov 24, 2022


Abstract:Numerous approaches have been proposed to discover causal dependencies in machine learning and data mining; among them, the state-of-the-art VAR-LiNGAM (short for Vector Auto-Regressive Linear Non-Gaussian Acyclic Model) is a desirable approach to reveal both the instantaneous and time-lagged relationships. However, all the obtained VAR matrices need to be analyzed to infer the final causal graph, leading to a rise in the number of parameters. To address this issue, we propose the CGP-LiNGAM (short for Causal Graph Process-LiNGAM), which has significantly fewer model parameters and deals with only one causal graph for interpreting the causal relations by exploiting Graph Signal Processing (GSP).
Learning Product Graphs from Spectral Templates
Nov 05, 2022Abstract:Graph Learning (GL) is at the core of inference and analysis of connections in data mining and machine learning (ML). By observing a dataset of graph signals, and considering specific assumptions, Graph Signal Processing (GSP) tools can provide practical constraints in the GL approach. One applicable constraint can infer a graph with desired frequency signatures, i.e., spectral templates. However, a severe computational burden is a challenging barrier, especially for inference from high-dimensional graph signals. To address this issue and in the case of the underlying graph having graph product structure, we propose learning product (high dimensional) graphs from product spectral templates with significantly reduced complexity rather than learning them directly from high-dimensional graph signals, which, to the best of our knowledge, has not been addressed in the related areas. In contrast to the rare current approaches, our approach can learn all types of product graphs (with more than two graphs) without knowing the type of graph products and has fewer parameters. Experimental results on both the synthetic and real-world data, i.e., brain signal analysis and multi-view object images, illustrate explainable and meaningful factor graphs supported by expert-related research, as well as outperforming the rare current restricted approaches.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge