Dynamic Triangulation-Based Graph Rewiring for Graph Neural Networks

Graph Neural Networks (GNNs) have emerged as the leading paradigm for learning over graph-structured data. However, their performance is limited by issues inherent to graph topology, most notably oversquashing and oversmoothing. Recent advances in graph rewiring aim to mitigate these limitations by modifying the graph topology to promote more effective information propagation. In this work, we introduce TRIGON, a novel framework that constructs enriched, non-planar triangulations by learning to select relevant triangles from multiple graph views. By jointly optimizing triangle selection and downstream classification performance, our method produces a rewired graph with markedly improved structural properties such as reduced diameter, increased spectral gap, and lower effective resistance compared to existing rewiring methods. Empirical results demonstrate that TRIGON outperforms state-of-the-art approaches on node classification tasks across a range of homophilic and heterophilic benchmarks.

Piecewise Constant Spectral Graph Neural Network

Graph Neural Networks (GNNs) have achieved significant success across various domains by leveraging graph structures in data. Existing spectral GNNs, which use low-degree polynomial filters to capture graph spectral properties, may not fully identify the graph's spectral characteristics because of the polynomial's small degree. However, increasing the polynomial degree is computationally expensive and beyond certain thresholds leads to performance plateaus or degradation. In this paper, we introduce the Piecewise Constant Spectral Graph Neural Network(PieCoN) to address these challenges. PieCoN combines constant spectral filters with polynomial filters to provide a more flexible way to leverage the graph structure. By adaptively partitioning the spectrum into intervals, our approach increases the range of spectral properties that can be effectively learned. Experiments on nine benchmark datasets, including both homophilic and heterophilic graphs, demonstrate that PieCoN is particularly effective on heterophilic datasets, highlighting its potential for a wide range of applications.

COSMOS: Continuous Simplicial Neural Networks

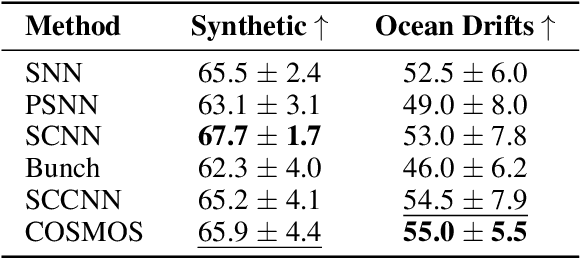
Simplicial complexes provide a powerful framework for modeling high-order interactions in structured data, making them particularly suitable for applications such as trajectory prediction and mesh processing. However, existing simplicial neural networks (SNNs), whether convolutional or attention-based, rely primarily on discrete filtering techniques, which can be restrictive. In contrast, partial differential equations (PDEs) on simplicial complexes offer a principled approach to capture continuous dynamics in such structures. In this work, we introduce COntinuous SiMplicial neural netwOrkS (COSMOS), a novel SNN architecture derived from PDEs on simplicial complexes. We provide theoretical and experimental justifications of COSMOS's stability under simplicial perturbations. Furthermore, we investigate the over-smoothing phenomenon, a common issue in geometric deep learning, demonstrating that COSMOS offers better control over this effect than discrete SNNs. Our experiments on real-world datasets of ocean trajectory prediction and regression on partial deformable shapes demonstrate that COSMOS achieves competitive performance compared to state-of-the-art SNNs in complex and noisy environments.

A Fused Gromov-Wasserstein Approach to Subgraph Contrastive Learning

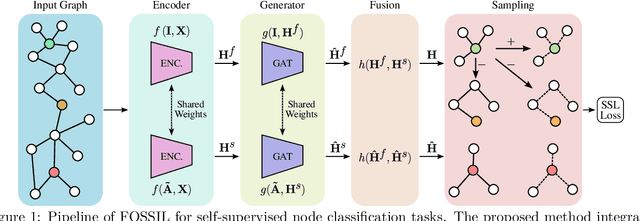
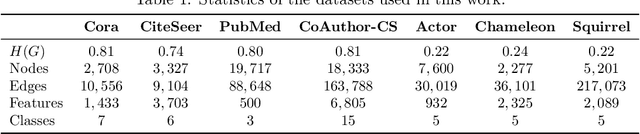
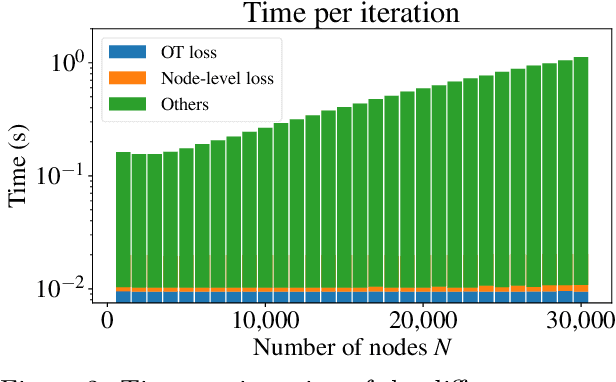
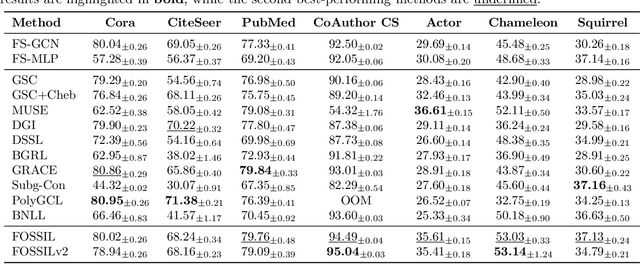
Self-supervised learning has become a key method for training deep learning models when labeled data is scarce or unavailable. While graph machine learning holds great promise across various domains, the design of effective pretext tasks for self-supervised graph representation learning remains challenging. Contrastive learning, a popular approach in graph self-supervised learning, leverages positive and negative pairs to compute a contrastive loss function. However, current graph contrastive learning methods often struggle to fully use structural patterns and node similarities. To address these issues, we present a new method called Fused Gromov Wasserstein Subgraph Contrastive Learning (FOSSIL). Our model integrates node-level and subgraph-level contrastive learning, seamlessly combining a standard node-level contrastive loss with the Fused Gromov-Wasserstein distance. This combination helps our method capture both node features and graph structure together. Importantly, our approach works well with both homophilic and heterophilic graphs and can dynamically create views for generating positive and negative pairs. Through extensive experiments on benchmark graph datasets, we show that FOSSIL outperforms or achieves competitive performance compared to current state-of-the-art methods.

Gaussian Mixture Models Based Augmentation Enhances GNN Generalization

Graph Neural Networks (GNNs) have shown great promise in tasks like node and graph classification, but they often struggle to generalize, particularly to unseen or out-of-distribution (OOD) data. These challenges are exacerbated when training data is limited in size or diversity. To address these issues, we introduce a theoretical framework using Rademacher complexity to compute a regret bound on the generalization error and then characterize the effect of data augmentation. This framework informs the design of GMM-GDA, an efficient graph data augmentation (GDA) algorithm leveraging the capability of Gaussian Mixture Models (GMMs) to approximate any distribution. Our approach not only outperforms existing augmentation techniques in terms of generalization but also offers improved time complexity, making it highly suitable for real-world applications.

Post-Hoc Robustness Enhancement in Graph Neural Networks with Conditional Random Fields

Graph Neural Networks (GNNs), which are nowadays the benchmark approach in graph representation learning, have been shown to be vulnerable to adversarial attacks, raising concerns about their real-world applicability. While existing defense techniques primarily concentrate on the training phase of GNNs, involving adjustments to message passing architectures or pre-processing methods, there is a noticeable gap in methods focusing on increasing robustness during inference. In this context, this study introduces RobustCRF, a post-hoc approach aiming to enhance the robustness of GNNs at the inference stage. Our proposed method, founded on statistical relational learning using a Conditional Random Field, is model-agnostic and does not require prior knowledge about the underlying model architecture. We validate the efficacy of this approach across various models, leveraging benchmark node classification datasets.

Higher-Order GNNs Meet Efficiency: Sparse Sobolev Graph Neural Networks

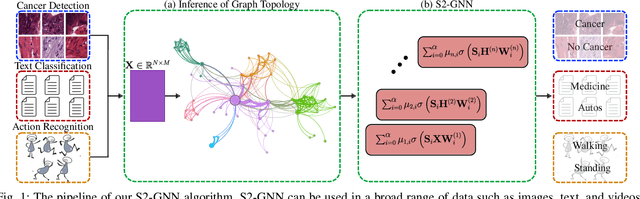
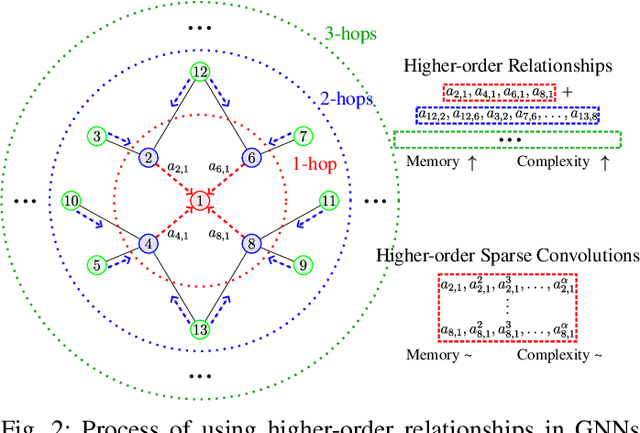
Graph Neural Networks (GNNs) have shown great promise in modeling relationships between nodes in a graph, but capturing higher-order relationships remains a challenge for large-scale networks. Previous studies have primarily attempted to utilize the information from higher-order neighbors in the graph, involving the incorporation of powers of the shift operator, such as the graph Laplacian or adjacency matrix. This approach comes with a trade-off in terms of increased computational and memory demands. Relying on graph spectral theory, we make a fundamental observation: the regular and the Hadamard power of the Laplacian matrix behave similarly in the spectrum. This observation has significant implications for capturing higher-order information in GNNs for various tasks such as node classification and semi-supervised learning. Consequently, we propose a novel graph convolutional operator based on the sparse Sobolev norm of graph signals. Our approach, known as Sparse Sobolev GNN (S2-GNN), employs Hadamard products between matrices to maintain the sparsity level in graph representations. S2-GNN utilizes a cascade of filters with increasing Hadamard powers to generate a diverse set of functions. We theoretically analyze the stability of S2-GNN to show the robustness of the model against possible graph perturbations. We also conduct a comprehensive evaluation of S2-GNN across various graph mining, semi-supervised node classification, and computer vision tasks. In particular use cases, our algorithm demonstrates competitive performance compared to state-of-the-art GNNs in terms of performance and running time.

Centrality Graph Shift Operators for Graph Neural Networks

Graph Shift Operators (GSOs), such as the adjacency and graph Laplacian matrices, play a fundamental role in graph theory and graph representation learning. Traditional GSOs are typically constructed by normalizing the adjacency matrix by the degree matrix, a local centrality metric. In this work, we instead propose and study Centrality GSOs (CGSOs), which normalize adjacency matrices by global centrality metrics such as the PageRank, $k$-core or count of fixed length walks. We study spectral properties of the CGSOs, allowing us to get an understanding of their action on graph signals. We confirm this understanding by defining and running the spectral clustering algorithm based on different CGSOs on several synthetic and real-world datasets. We furthermore outline how our CGSO can act as the message passing operator in any Graph Neural Network and in particular demonstrate strong performance of a variant of the Graph Convolutional Network and Graph Attention Network using our CGSOs on several real-world benchmark datasets.

How Fair is Your Diffusion Recommender Model?

Diffusion-based recommender systems have recently proven to outperform traditional generative recommendation approaches, such as variational autoencoders and generative adversarial networks. Nevertheless, the machine learning literature has raised several concerns regarding the possibility that diffusion models, while learning the distribution of data samples, may inadvertently carry information bias and lead to unfair outcomes. In light of this aspect, and considering the relevance that fairness has held in recommendations over the last few decades, we conduct one of the first fairness investigations in the literature on DiffRec, a pioneer approach in diffusion-based recommendation. First, we propose an experimental setting involving DiffRec (and its variant L-DiffRec) along with nine state-of-the-art recommendation models, two popular recommendation datasets from the fairness-aware literature, and six metrics accounting for accuracy and consumer/provider fairness. Then, we perform a twofold analysis, one assessing models' performance under accuracy and recommendation fairness separately, and the other identifying if and to what extent such metrics can strike a performance trade-off. Experimental results from both studies confirm the initial unfairness warnings but pave the way for how to address them in future research directions.

Do We Really Need to Drop Items with Missing Modalities in Multimodal Recommendation?

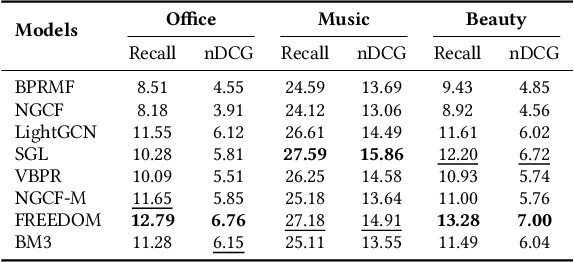
Generally, items with missing modalities are dropped in multimodal recommendation. However, with this work, we question this procedure, highlighting that it would further damage the pipeline of any multimodal recommender system. First, we show that the lack of (some) modalities is, in fact, a widely-diffused phenomenon in multimodal recommendation. Second, we propose a pipeline that imputes missing multimodal features in recommendation by leveraging traditional imputation strategies in machine learning. Then, given the graph structure of the recommendation data, we also propose three more effective imputation solutions that leverage the item-item co-purchase graph and the multimodal similarities of co-interacted items. Our method can be plugged into any multimodal RSs in the literature working as an untrained pre-processing phase, showing (through extensive experiments) that any data pre-filtering is not only unnecessary but also harmful to the performance.