Geometry-Induced Long-Range Correlations in Recurrent Neural Network Quantum States

Neural Quantum States based on autoregressive recurrent neural network (RNN) wave functions enable efficient sampling without Markov-chain autocorrelation, but standard RNN architectures are biased toward finite-length correlations and can fail on states with long-range dependencies. A common response is to adopt transformer-style self-attention, but this typically comes with substantially higher computational and memory overhead. Here we introduce dilated RNN wave functions, where recurrent units access distant sites through dilated connections, injecting an explicit long-range inductive bias while retaining a favorable $\mathcal{O}(N \log N)$ forward pass scaling. We show analytically that dilation changes the correlation geometry and can induce power-law correlation scaling in a simplified linearized and perturbative setting. Numerically, for the critical 1D transverse-field Ising model, dilated RNNs reproduce the expected power-law connected two-point correlations in contrast to the exponential decay typical of conventional RNN ansätze. We further show that the dilated RNN accurately approximates the one-dimensional Cluster state, a paradigmatic example with long-range conditional correlations that has previously been reported to be challenging for RNN-based wave functions. These results highlight dilation as a simple geometric mechanism for building correlation-aware autoregressive neural quantum states.

Are GNNs doomed by the topology of their input graph?

Graph Neural Networks (GNNs) have demonstrated remarkable success in learning from graph-structured data. However, the influence of the input graph's topology on GNN behavior remains poorly understood. In this work, we explore whether GNNs are inherently limited by the structure of their input graphs, focusing on how local topological features interact with the message-passing scheme to produce global phenomena such as oversmoothing or expressive representations. We introduce the concept of $k$-hop similarity and investigate whether locally similar neighborhoods lead to consistent node representations. This interaction can result in either effective learning or inevitable oversmoothing, depending on the inherent properties of the graph. Our empirical experiments validate these insights, highlighting the practical implications of graph topology on GNN performance.

GeLoRA: Geometric Adaptive Ranks For Efficient LoRA Fine-tuning

Fine-tuning large language models (LLMs) is computationally intensive because it requires updating all parameters. Low-Rank Adaptation (LoRA) improves efficiency by modifying only a subset of weights but introduces a trade-off between expressivity and computational cost: lower ranks reduce resources but limit expressiveness, while higher ranks enhance expressivity at increased cost. Despite recent advances in adaptive LoRA techniques, existing methods fail to provide a theoretical basis for optimizing the trade-off between model performance and efficiency. We propose Geometric Low-Rank Adaptation (GeLoRA), a novel framework that computes the intrinsic dimensionality of hidden state representations to adaptively select LoRA ranks. We demonstrate that the intrinsic dimension provides a lower bound for the optimal rank of LoRA matrices, allowing for a principled selection that balances efficiency and expressivity. GeLoRA dynamically adjusts the rank for each layer based on the intrinsic dimensionality of its input and output representations, recognizing that not all model parameters equally impact fine-tuning. Empirical validation on multiple tasks shows that GeLoRA consistently outperforms recent baselines within the same parameter budget.

Gaussian Mixture Models Based Augmentation Enhances GNN Generalization

Graph Neural Networks (GNNs) have shown great promise in tasks like node and graph classification, but they often struggle to generalize, particularly to unseen or out-of-distribution (OOD) data. These challenges are exacerbated when training data is limited in size or diversity. To address these issues, we introduce a theoretical framework using Rademacher complexity to compute a regret bound on the generalization error and then characterize the effect of data augmentation. This framework informs the design of GMM-GDA, an efficient graph data augmentation (GDA) algorithm leveraging the capability of Gaussian Mixture Models (GMMs) to approximate any distribution. Our approach not only outperforms existing augmentation techniques in terms of generalization but also offers improved time complexity, making it highly suitable for real-world applications.

Don't overfit the history -- Recursive time series data augmentation

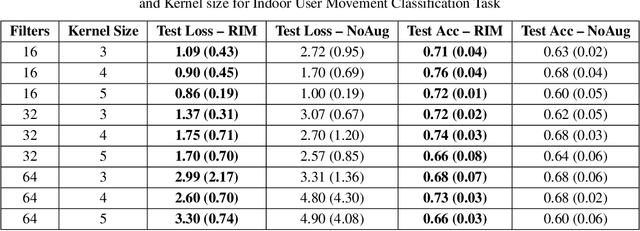
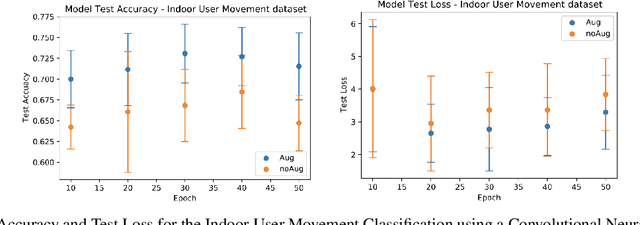
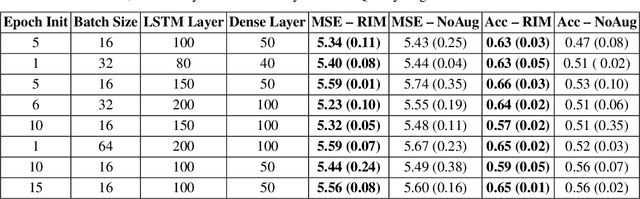
Time series observations can be seen as realizations of an underlying dynamical system governed by rules that we typically do not know. For time series learning tasks, we need to understand that we fit our model on available data, which is a unique realized history. Training on a single realization often induces severe overfitting lacking generalization. To address this issue, we introduce a general recursive framework for time series augmentation, which we call Recursive Interpolation Method, denoted as RIM. New samples are generated using a recursive interpolation function of all previous values in such a way that the enhanced samples preserve the original inherent time series dynamics. We perform theoretical analysis to characterize the proposed RIM and to guarantee its test performance. We apply RIM to diverse real world time series cases to achieve strong performance over non-augmented data on regression, classification, and reinforcement learning tasks.

A Deep Reinforcement Learning Framework For Column Generation

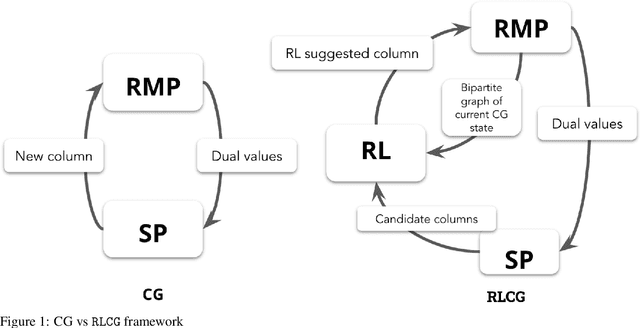
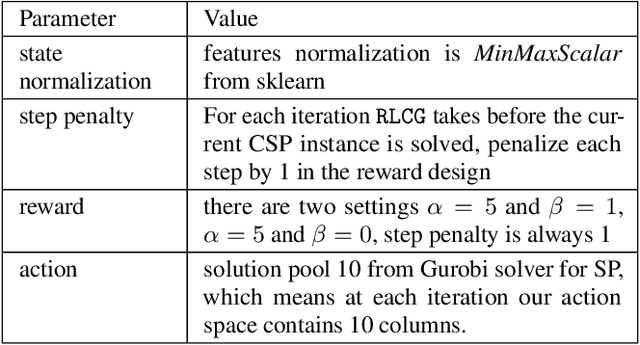
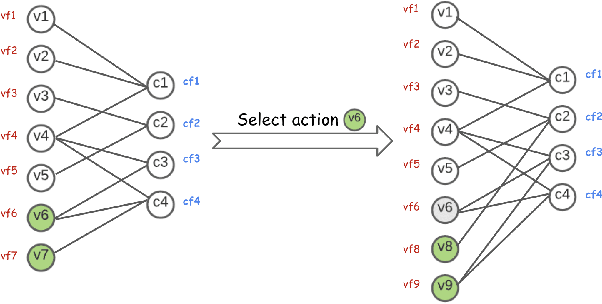
Column Generation (CG) is an iterative algorithm for solving linear programs (LPs) with an extremely large number of variables (columns). CG is the workhorse for tackling large-scale integer linear programs, which rely on CG to solve LP relaxations within a branch and bound algorithm. Two canonical applications are the Cutting Stock Problem (CSP) and Vehicle Routing Problem with Time Windows (VRPTW). In VRPTW, for example, each binary variable represents the decision to include or exclude a route, of which there are exponentially many; CG incrementally grows the subset of columns being used, ultimately converging to an optimal solution. We propose RLCG, the first Reinforcement Learning (RL) approach for CG. Unlike typical column selection rules which myopically select a column based on local information at each iteration, we treat CG as a sequential decision-making problem, as the column selected in an iteration affects subsequent iterations of the algorithm. This perspective lends itself to a Deep Reinforcement Learning approach that uses Graph Neural Networks (GNNs) to represent the variable-constraint structure in the LP of interest. We perform an extensive set of experiments using the publicly available BPPLIB benchmark for CSP and Solomon benchmark for VRPTW. RLCG converges faster and reduces the number of CG iterations by 22.4% for CSP and 40.9% for VRPTW on average compared to a commonly used greedy policy.