Elias B. Khalil
Self-Supervised Transformers as Iterative Solution Improvers for Constraint Satisfaction
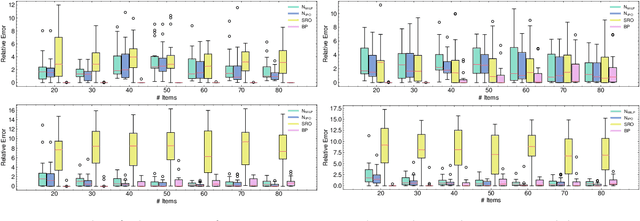
Feb 18, 2025Abstract:We present a Transformer-based framework for Constraint Satisfaction Problems (CSPs). CSPs find use in many applications and thus accelerating their solution with machine learning is of wide interest. Most existing approaches rely on supervised learning from feasible solutions or reinforcement learning, paradigms that require either feasible solutions to these NP-Complete CSPs or large training budgets and a complex expert-designed reward signal. To address these challenges, we propose ConsFormer, a self-supervised framework that leverages a Transformer as a solution refiner. ConsFormer constructs a solution to a CSP iteratively in a process that mimics local search. Instead of using feasible solutions as labeled data, we devise differentiable approximations to the discrete constraints of a CSP to guide model training. Our model is trained to improve random assignments for a single step but is deployed iteratively at test time, circumventing the bottlenecks of supervised and reinforcement learning. Our method can tackle out-of-distribution CSPs simply through additional iterations.
Learning to Optimize for Mixed-Integer Non-linear Programming
Oct 14, 2024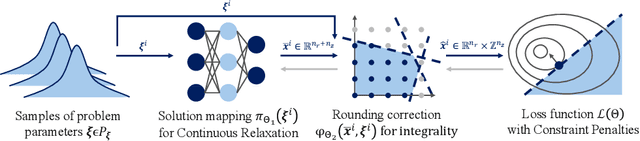
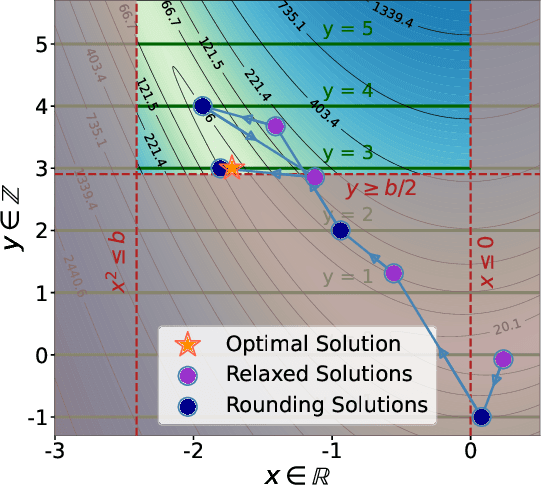
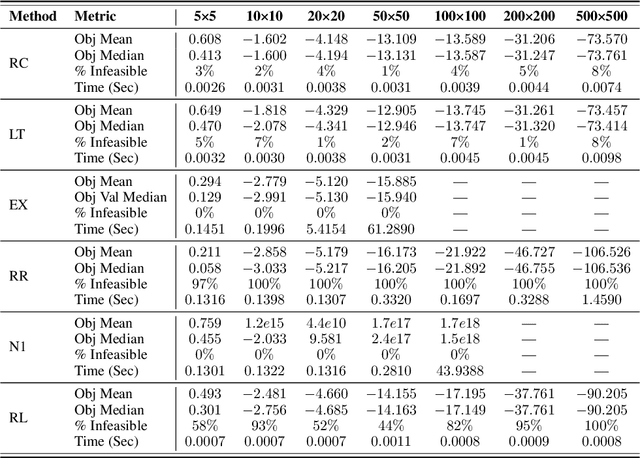
Abstract:Mixed-integer non-linear programs (MINLPs) arise in various domains, such as energy systems and transportation, but are notoriously difficult to solve. Recent advances in machine learning have led to remarkable successes in optimization tasks, an area broadly known as learning to optimize. This approach includes using predictive models to generate solutions for optimization problems with continuous decision variables, thereby avoiding the need for computationally expensive optimization algorithms. However, applying learning to MINLPs remains challenging primarily due to the presence of integer decision variables, which complicate gradient-based learning. To address this limitation, we propose two differentiable correction layers that generate integer outputs while preserving gradient information. Combined with a soft penalty for constraint violation, our framework can tackle both the integrality and non-linear constraints in a MINLP. Experiments on three problem classes with convex/non-convex objective/constraints and integer/mixed-integer variables show that the proposed learning-based approach consistently produces high-quality solutions for parametric MINLPs extremely quickly. As problem size increases, traditional exact solvers and heuristic methods struggle to find feasible solutions, whereas our approach continues to deliver reliable results. Our work extends the scope of learning-to-optimize to MINLP, paving the way for integrating integer constraints into deep learning models. Our code is available at https://github.com/pnnl/L2O-pMINLP.
Learn2Aggregate: Supervised Generation of Chvátal-Gomory Cuts Using Graph Neural Networks
Sep 10, 2024
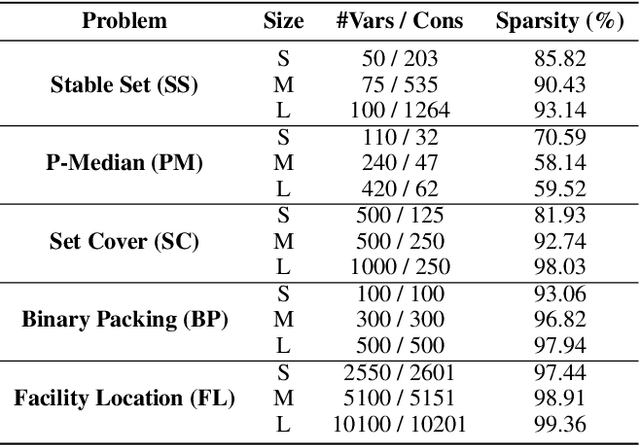
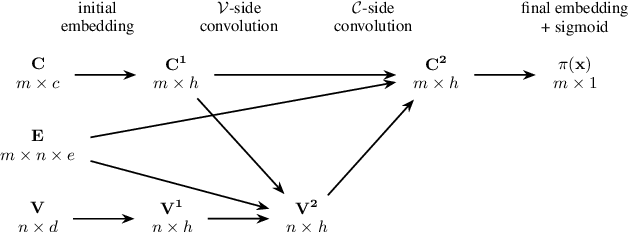
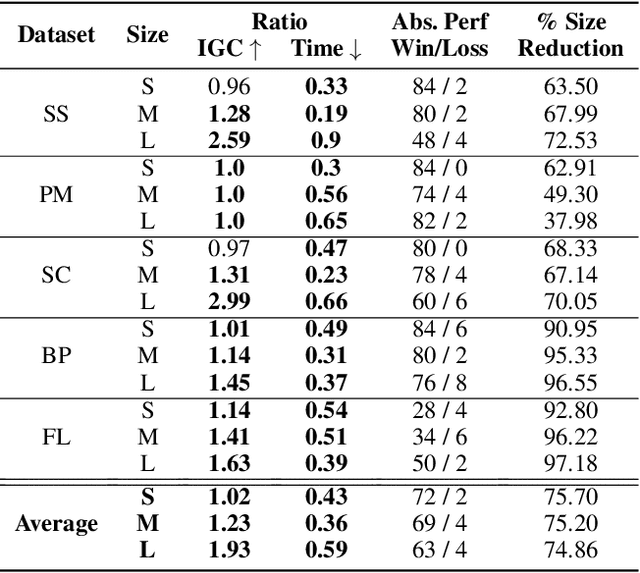
Abstract:We present $\textit{Learn2Aggregate}$, a machine learning (ML) framework for optimizing the generation of Chv\'atal-Gomory (CG) cuts in mixed integer linear programming (MILP). The framework trains a graph neural network to classify useful constraints for aggregation in CG cut generation. The ML-driven CG separator selectively focuses on a small set of impactful constraints, improving runtimes without compromising the strength of the generated cuts. Key to our approach is the formulation of a constraint classification task which favours sparse aggregation of constraints, consistent with empirical findings. This, in conjunction with a careful constraint labeling scheme and a hybrid of deep learning and feature engineering, results in enhanced CG cut generation across five diverse MILP benchmarks. On the largest test sets, our method closes roughly $\textit{twice}$ as much of the integrality gap as the standard CG method while running 40$% faster. This performance improvement is due to our method eliminating 75% of the constraints prior to aggregation.
MORBDD: Multiobjective Restricted Binary Decision Diagrams by Learning to Sparsify
Mar 04, 2024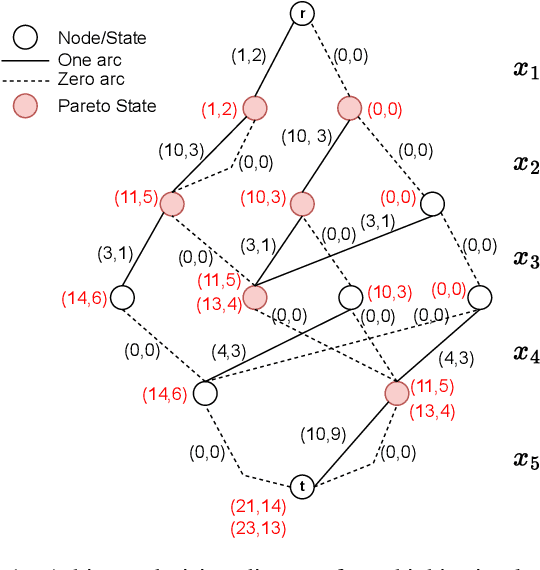

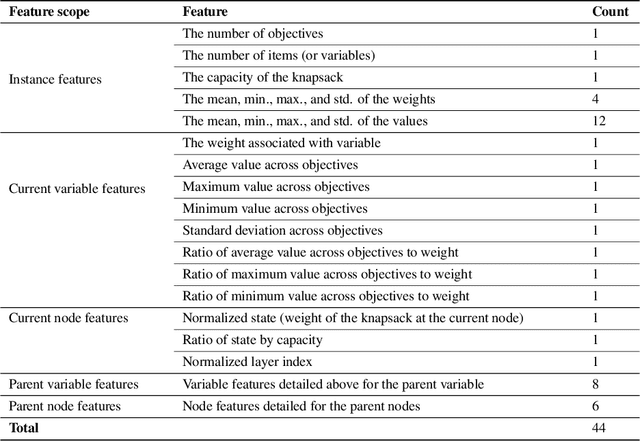
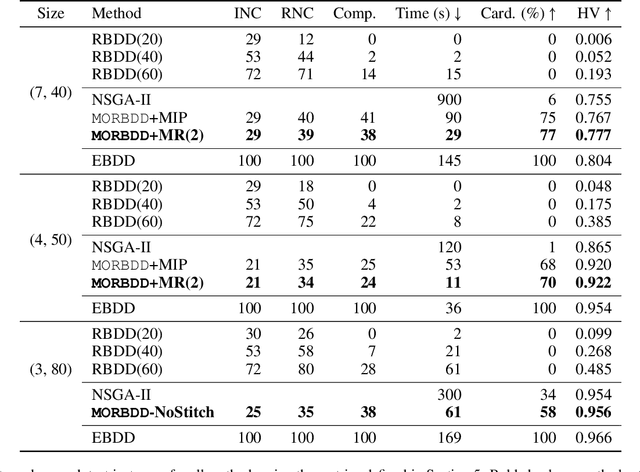
Abstract:In multicriteria decision-making, a user seeks a set of non-dominated solutions to a (constrained) multiobjective optimization problem, the so-called Pareto frontier. In this work, we seek to bring a state-of-the-art method for exact multiobjective integer linear programming into the heuristic realm. We focus on binary decision diagrams (BDDs) which first construct a graph that represents all feasible solutions to the problem and then traverse the graph to extract the Pareto frontier. Because the Pareto frontier may be exponentially large, enumerating it over the BDD can be time-consuming. We explore how restricted BDDs, which have already been shown to be effective as heuristics for single-objective problems, can be adapted to multiobjective optimization through the use of machine learning (ML). MORBDD, our ML-based BDD sparsifier, first trains a binary classifier to eliminate BDD nodes that are unlikely to contribute to Pareto solutions, then post-processes the sparse BDD to ensure its connectivity via optimization. Experimental results on multiobjective knapsack problems show that MORBDD is highly effective at producing very small restricted BDDs with excellent approximation quality, outperforming width-limited restricted BDDs and the well-known evolutionary algorithm NSGA-II.
Neur2BiLO: Neural Bilevel Optimization
Feb 04, 2024



Abstract:Bilevel optimization deals with nested problems in which a leader takes the first decision to minimize their objective function while accounting for a follower's best-response reaction. Constrained bilevel problems with integer variables are particularly notorious for their hardness. While exact solvers have been proposed for mixed-integer linear bilevel optimization, they tend to scale poorly with problem size and are hard to generalize to the non-linear case. On the other hand, problem-specific algorithms (exact and heuristic) are limited in scope. Under a data-driven setting in which similar instances of a bilevel problem are solved routinely, our proposed framework, Neur2BiLO, embeds a neural network approximation of the leader's or follower's value function, trained via supervised regression, into an easy-to-solve mixed-integer program. Neur2BiLO serves as a heuristic that produces high-quality solutions extremely fast for the bilevel knapsack interdiction problem, the "critical node game" from network security, a donor-recipient healthcare problem, and discrete network design from transportation planning. These problems are diverse in that they have linear or non-linear objectives/constraints and integer or mixed-integer variables, making Neur2BiLO unique in its versatility.
CaVE: A Cone-Aligned Approach for Fast Predict-then-optimize with Binary Linear Programs
Dec 12, 2023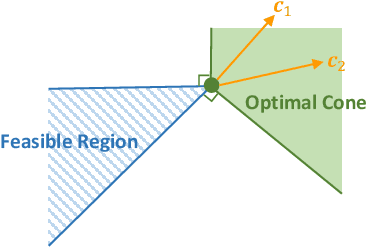

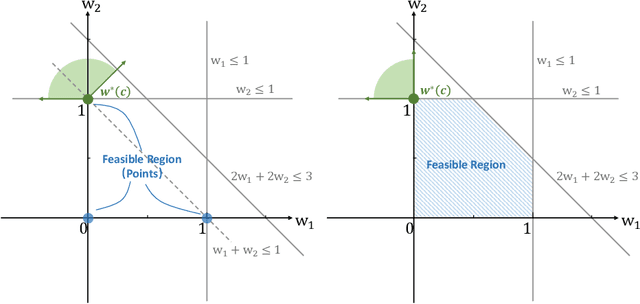
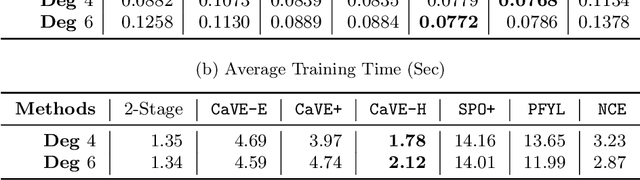
Abstract:The end-to-end predict-then-optimize framework, also known as decision-focused learning, has gained popularity for its ability to integrate optimization into the training procedure of machine learning models that predict the unknown cost (objective function) coefficients of optimization problems from contextual instance information. Naturally, most of the problems of interest in this space can be cast as integer linear programs. In this work, we focus on binary linear programs (BLPs) and propose a new end-to-end training method for predict-then-optimize. Our method, Cone-aligned Vector Estimation (CaVE), aligns the predicted cost vectors with the cone corresponding to the true optimal solution of a training instance. When the predicted cost vector lies inside the cone, the optimal solution to the linear relaxation of the binary problem is optimal w.r.t. to the true cost vector. Not only does this alignment produce decision-aware learning models, but it also dramatically reduces training time as it circumvents the need to solve BLPs to compute a loss function with its gradients. Experiments across multiple datasets show that our method exhibits a favorable trade-off between training time and solution quality, particularly with large-scale optimization problems such as vehicle routing, a hard BLP that has yet to benefit from predict-then-optimize methods in the literature due to its difficulty.
Neur2RO: Neural Two-Stage Robust Optimization
Oct 06, 2023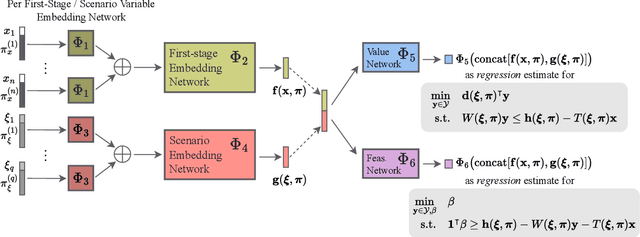
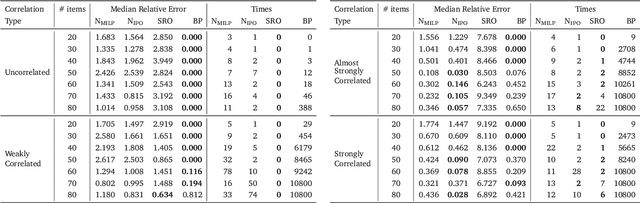
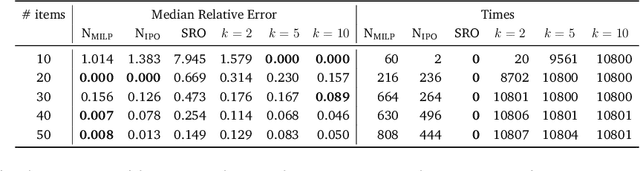
Abstract:Robust optimization provides a mathematical framework for modeling and solving decision-making problems under worst-case uncertainty. This work addresses two-stage robust optimization (2RO) problems (also called adjustable robust optimization), wherein first-stage and second-stage decisions are made before and after uncertainty is realized, respectively. This results in a nested min-max-min optimization problem which is extremely challenging computationally, especially when the decisions are discrete. We propose Neur2RO, an efficient machine learning-driven instantiation of column-and-constraint generation (CCG), a classical iterative algorithm for 2RO. Specifically, we learn to estimate the value function of the second-stage problem via a novel neural network architecture that is easy to optimize over by design. Embedding our neural network into CCG yields high-quality solutions quickly as evidenced by experiments on two 2RO benchmarks, knapsack and capital budgeting. For knapsack, Neur2RO finds solutions that are within roughly $2\%$ of the best-known values in a few seconds compared to the three hours of the state-of-the-art exact branch-and-price algorithm; for larger and more complex instances, Neur2RO finds even better solutions. For capital budgeting, Neur2RO outperforms three variants of the $k$-adaptability algorithm, particularly on the largest instances, with a 5 to 10-fold reduction in solution time. Our code and data are available at https://github.com/khalil-research/Neur2RO.
LEO: Learning Efficient Orderings for Multiobjective Binary Decision Diagrams
Jul 06, 2023



Abstract:Approaches based on Binary decision diagrams (BDDs) have recently achieved state-of-the-art results for multiobjective integer programming problems. The variable ordering used in constructing BDDs can have a significant impact on their size and on the quality of bounds derived from relaxed or restricted BDDs for single-objective optimization problems. We first showcase a similar impact of variable ordering on the Pareto frontier (PF) enumeration time for the multiobjective knapsack problem, suggesting the need for deriving variable ordering methods that improve the scalability of the multiobjective BDD approach. To that end, we derive a novel parameter configuration space based on variable scoring functions which are linear in a small set of interpretable and easy-to-compute variable features. We show how the configuration space can be efficiently explored using black-box optimization, circumventing the curse of dimensionality (in the number of variables and objectives), and finding good orderings that reduce the PF enumeration time. However, black-box optimization approaches incur a computational overhead that outweighs the reduction in time due to good variable ordering. To alleviate this issue, we propose LEO, a supervised learning approach for finding efficient variable orderings that reduce the enumeration time. Experiments on benchmark sets from the knapsack problem with 3-7 objectives and up to 80 variables show that LEO is ~30-300% and ~10-200% faster at PF enumeration than common ordering strategies and algorithm configuration. Our code and instances are available at https://github.com/khalil-research/leo.
Fast Matrix Multiplication Without Tears: A Constraint Programming Approach
Jun 01, 2023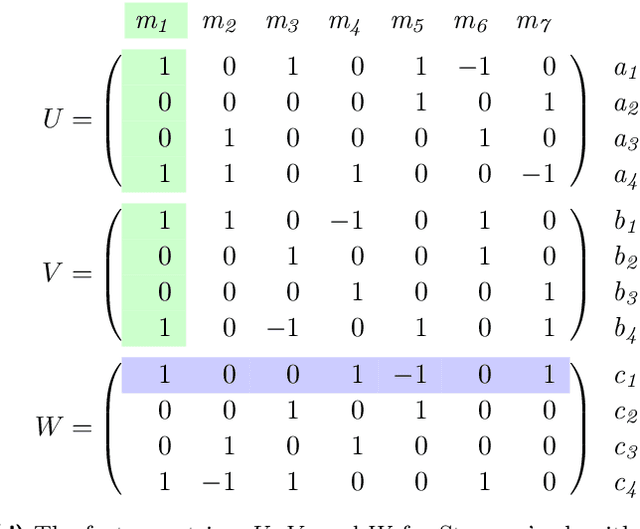
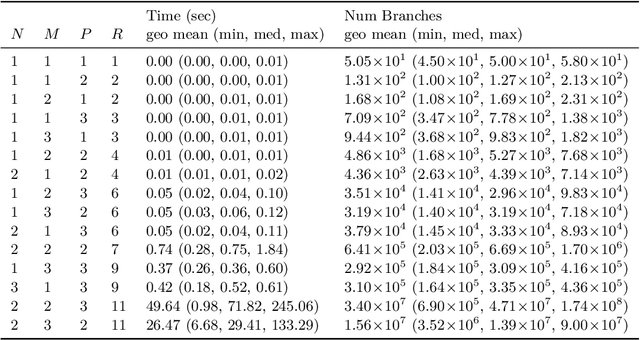
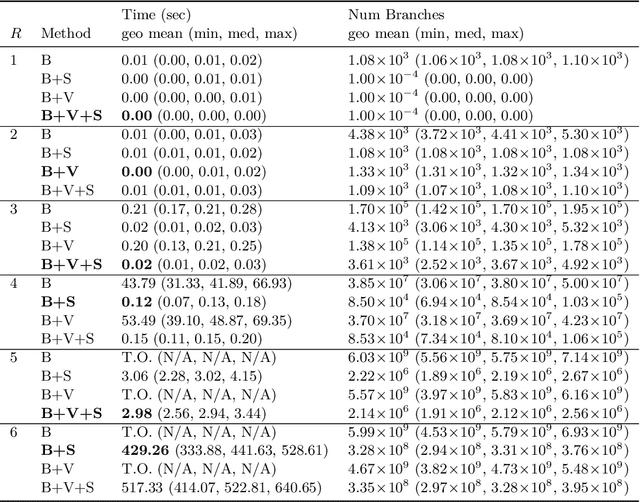

Abstract:It is known that the multiplication of an $N \times M$ matrix with an $M \times P$ matrix can be performed using fewer multiplications than what the naive $NMP$ approach suggests. The most famous instance of this is Strassen's algorithm for multiplying two $2\times 2$ matrices in 7 instead of 8 multiplications. This gives rise to the constraint satisfaction problem of fast matrix multiplication, where a set of $R < NMP$ multiplication terms must be chosen and combined such that they satisfy correctness constraints on the output matrix. Despite its highly combinatorial nature, this problem has not been exhaustively examined from that perspective, as evidenced for example by the recent deep reinforcement learning approach of AlphaTensor. In this work, we propose a simple yet novel Constraint Programming approach to find non-commutative algorithms for fast matrix multiplication or provide proof of infeasibility otherwise. We propose a set of symmetry-breaking constraints and valid inequalities that are particularly helpful in proving infeasibility. On the feasible side, we find that exploiting solver performance variability in conjunction with a sparsity-based problem decomposition enables finding solutions for larger (feasible) instances of fast matrix multiplication. Our experimental results using CP Optimizer demonstrate that we can find fast matrix multiplication algorithms for matrices up to $3\times 3$ in a short amount of time.
LLMs and the Abstraction and Reasoning Corpus: Successes, Failures, and the Importance of Object-based Representations
May 26, 2023Abstract:Can a Large Language Model (LLM) solve simple abstract reasoning problems? We explore this broad question through a systematic analysis of GPT on the Abstraction and Reasoning Corpus (ARC), a representative benchmark of abstract reasoning ability from limited examples in which solutions require some "core knowledge" of concepts such as objects, goal states, counting, and basic geometry. GPT-4 solves only 13/50 of the most straightforward ARC tasks when using textual encodings for their two-dimensional input-output grids. Our failure analysis reveals that GPT-4's capacity to identify objects and reason about them is significantly influenced by the sequential nature of the text that represents an object within a text encoding of a task. To test this hypothesis, we design a new benchmark, the 1D-ARC, which consists of one-dimensional (array-like) tasks that are more conducive to GPT-based reasoning, and where it indeed performs better than on the (2D) ARC. To alleviate this issue, we propose an object-based representation that is obtained through an external tool, resulting in nearly doubling the performance on solved ARC tasks and near-perfect scores on the easier 1D-ARC. Although the state-of-the-art GPT-4 is unable to "reason" perfectly within non-language domains such as the 1D-ARC or a simple ARC subset, our study reveals that the use of object-based representations can significantly improve its reasoning ability. Visualizations, GPT logs, and data are available at https://khalil-research.github.io/LLM4ARC.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge