CaVE: A Cone-Aligned Approach for Fast Predict-then-optimize with Binary Linear Programs

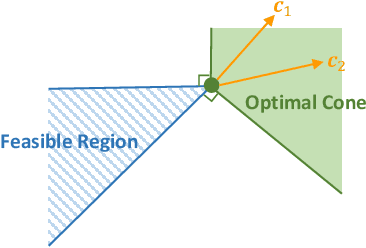
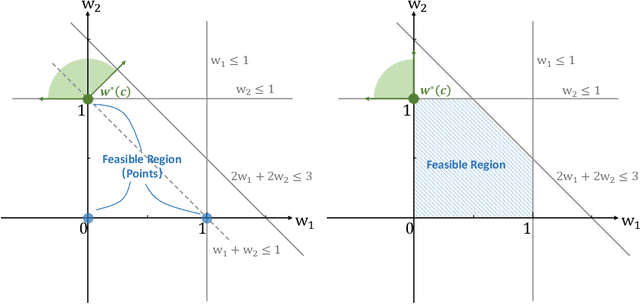
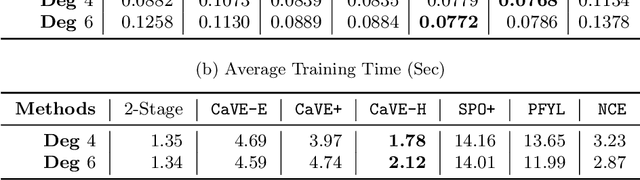
The end-to-end predict-then-optimize framework, also known as decision-focused learning, has gained popularity for its ability to integrate optimization into the training procedure of machine learning models that predict the unknown cost (objective function) coefficients of optimization problems from contextual instance information. Naturally, most of the problems of interest in this space can be cast as integer linear programs. In this work, we focus on binary linear programs (BLPs) and propose a new end-to-end training method for predict-then-optimize. Our method, Cone-aligned Vector Estimation (CaVE), aligns the predicted cost vectors with the cone corresponding to the true optimal solution of a training instance. When the predicted cost vector lies inside the cone, the optimal solution to the linear relaxation of the binary problem is optimal w.r.t. to the true cost vector. Not only does this alignment produce decision-aware learning models, but it also dramatically reduces training time as it circumvents the need to solve BLPs to compute a loss function with its gradients. Experiments across multiple datasets show that our method exhibits a favorable trade-off between training time and solution quality, particularly with large-scale optimization problems such as vehicle routing, a hard BLP that has yet to benefit from predict-then-optimize methods in the literature due to its difficulty.