MORBDD: Multiobjective Restricted Binary Decision Diagrams by Learning to Sparsify
Paper and Code
Mar 04, 2024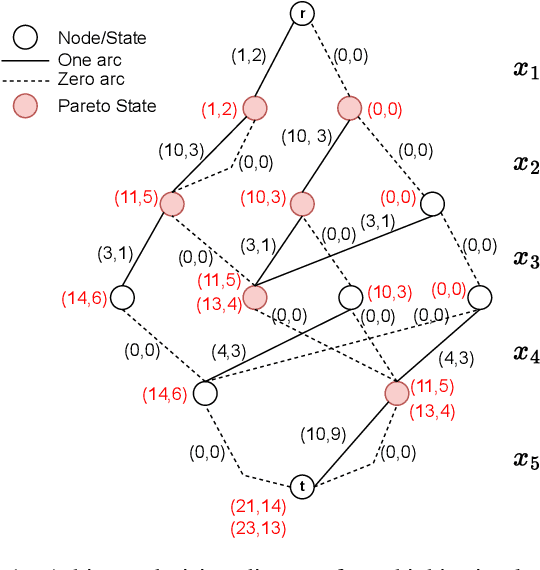

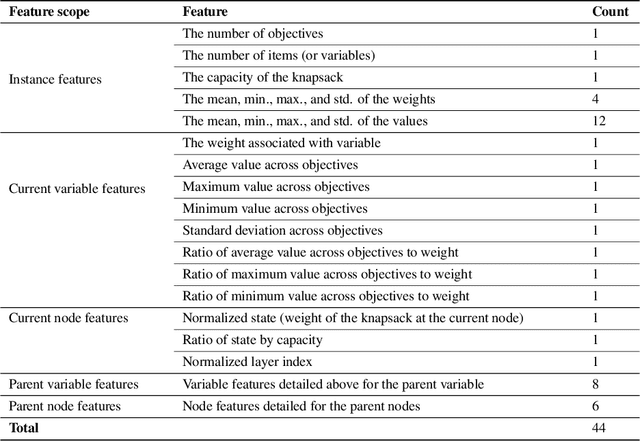
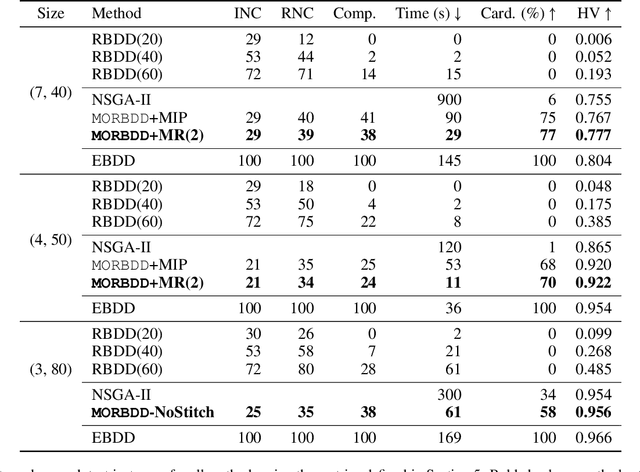
In multicriteria decision-making, a user seeks a set of non-dominated solutions to a (constrained) multiobjective optimization problem, the so-called Pareto frontier. In this work, we seek to bring a state-of-the-art method for exact multiobjective integer linear programming into the heuristic realm. We focus on binary decision diagrams (BDDs) which first construct a graph that represents all feasible solutions to the problem and then traverse the graph to extract the Pareto frontier. Because the Pareto frontier may be exponentially large, enumerating it over the BDD can be time-consuming. We explore how restricted BDDs, which have already been shown to be effective as heuristics for single-objective problems, can be adapted to multiobjective optimization through the use of machine learning (ML). MORBDD, our ML-based BDD sparsifier, first trains a binary classifier to eliminate BDD nodes that are unlikely to contribute to Pareto solutions, then post-processes the sparse BDD to ensure its connectivity via optimization. Experimental results on multiobjective knapsack problems show that MORBDD is highly effective at producing very small restricted BDDs with excellent approximation quality, outperforming width-limited restricted BDDs and the well-known evolutionary algorithm NSGA-II.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge