MORBDD: Multiobjective Restricted Binary Decision Diagrams by Learning to Sparsify

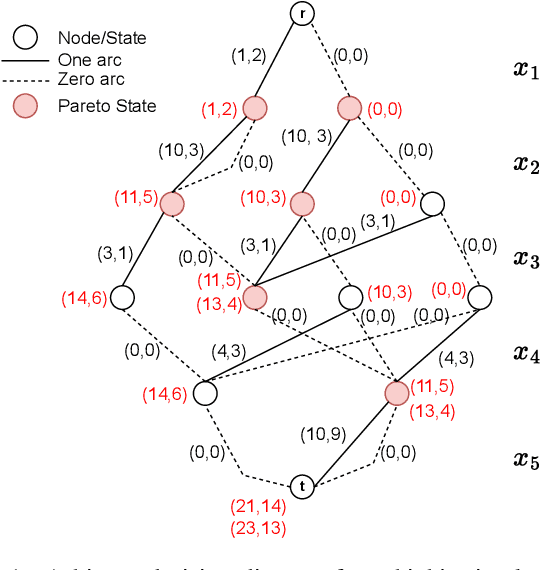
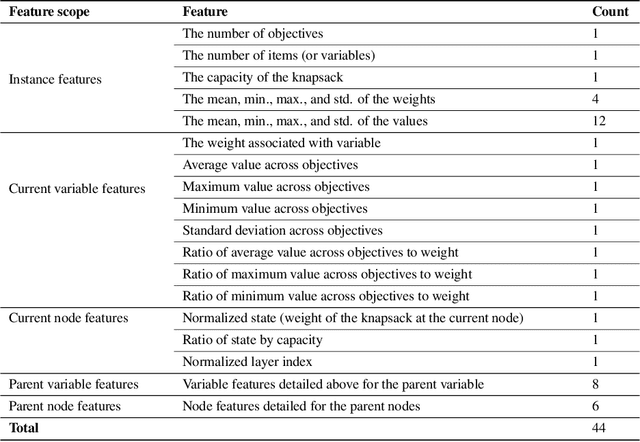
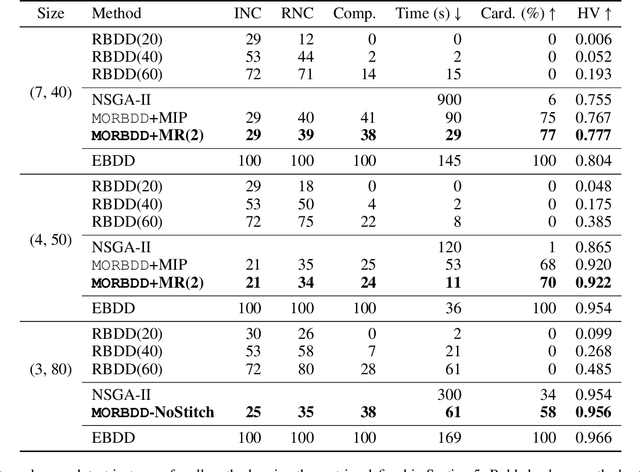
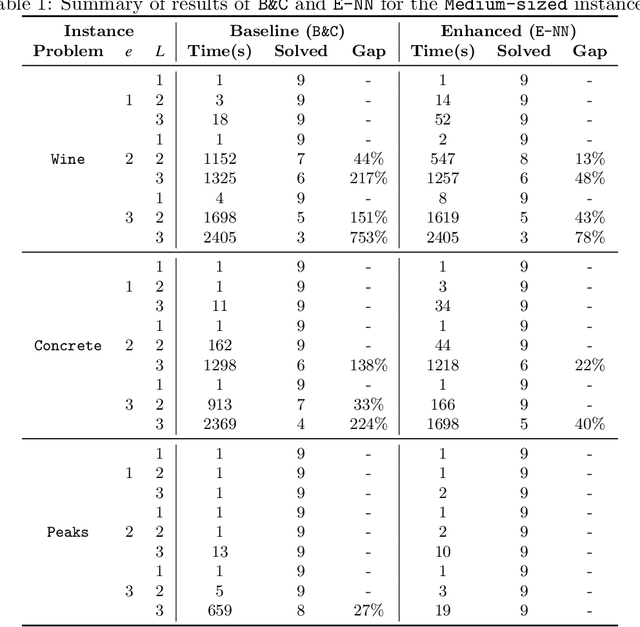
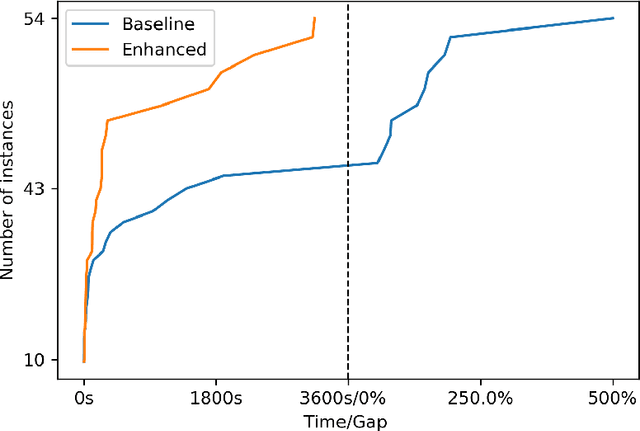
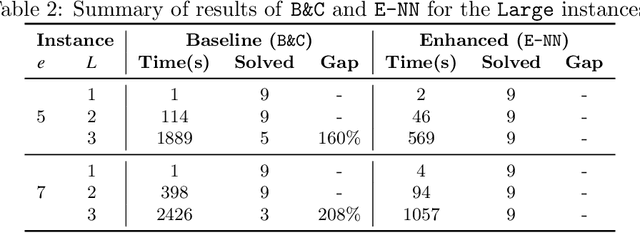
In multicriteria decision-making, a user seeks a set of non-dominated solutions to a (constrained) multiobjective optimization problem, the so-called Pareto frontier. In this work, we seek to bring a state-of-the-art method for exact multiobjective integer linear programming into the heuristic realm. We focus on binary decision diagrams (BDDs) which first construct a graph that represents all feasible solutions to the problem and then traverse the graph to extract the Pareto frontier. Because the Pareto frontier may be exponentially large, enumerating it over the BDD can be time-consuming. We explore how restricted BDDs, which have already been shown to be effective as heuristics for single-objective problems, can be adapted to multiobjective optimization through the use of machine learning (ML). MORBDD, our ML-based BDD sparsifier, first trains a binary classifier to eliminate BDD nodes that are unlikely to contribute to Pareto solutions, then post-processes the sparse BDD to ensure its connectivity via optimization. Experimental results on multiobjective knapsack problems show that MORBDD is highly effective at producing very small restricted BDDs with excellent approximation quality, outperforming width-limited restricted BDDs and the well-known evolutionary algorithm NSGA-II.

BDD for Complete Characterization of a Safety Violation in Linear Systems with Inputs

The control design tools for linear systems typically involves pole placement and computing Lyapunov functions which are useful for ensuring stability. But given higher requirements on control design, a designer is expected to satisfy other specification such as safety or temporal logic specification as well, and a naive control design might not satisfy such specification. A control designer can employ model checking as a tool for checking safety and obtain a counterexample in case of a safety violation. While several scalable techniques for verification have been developed for safety verification of linear dynamical systems, such tools merely act as decision procedures to evaluate system safety and, consequently, yield a counterexample as an evidence to safety violation. However these model checking methods are not geared towards discovering corner cases or re-using verification artifacts for another sub-optimal safety specification. In this paper, we describe a technique for obtaining complete characterization of counterexamples for a safety violation in linear systems. The proposed technique uses the reachable set computed during safety verification for a given temporal logic formula, performs constraint propagation, and represents all modalities of counterexamples using a binary decision diagram (BDD). We introduce an approach to dynamically determine isomorphic nodes for obtaining a considerably reduced (in size) decision diagram. A thorough experimental evaluation on various benchmarks exhibits that the reduction technique achieves up to $67\%$ reduction in the number of nodes and $75\%$ reduction in the width of the decision diagram.

Careful! Training Relevance is Real

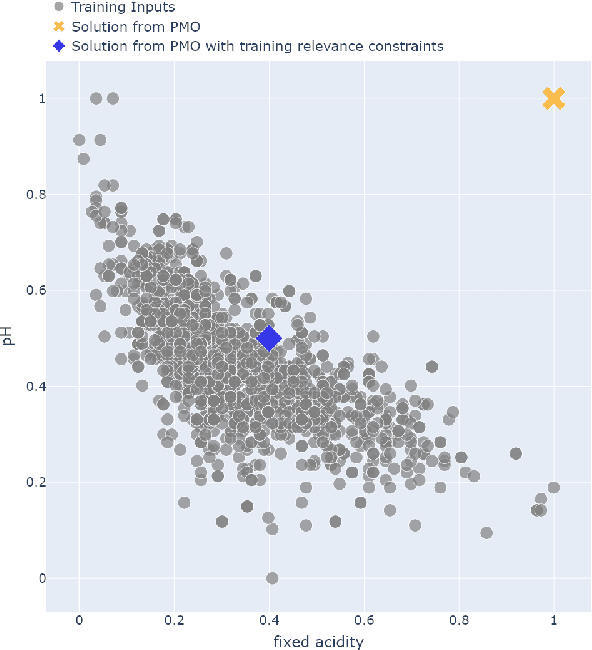
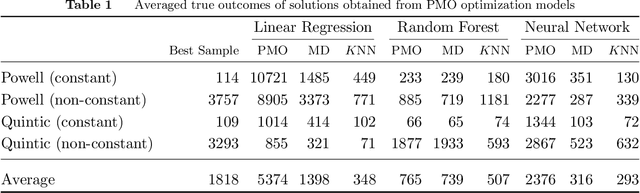
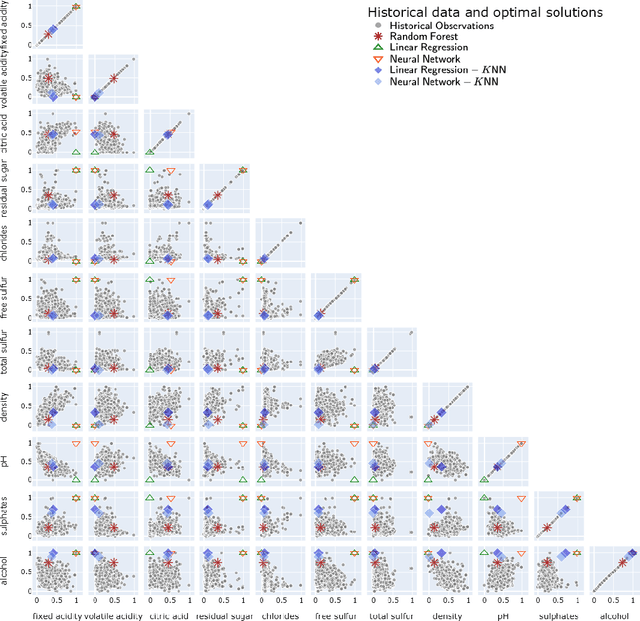
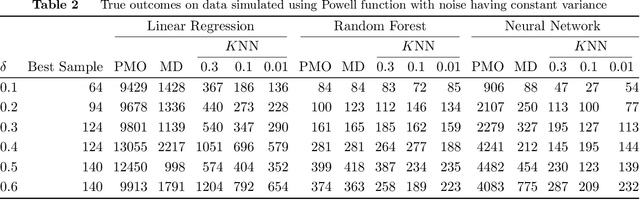
There is a recent proliferation of research on the integration of machine learning and optimization. One expansive area within this research stream is predictive-model embedded optimization, which uses pre-trained predictive models for the objective function of an optimization problem, so that features of the predictive models become decision variables in the optimization problem. Despite a recent surge in publications in this area, one aspect of this decision-making pipeline that has been largely overlooked is training relevance, i.e., ensuring that solutions to the optimization problem should be similar to the data used to train the predictive models. In this paper, we propose constraints designed to enforce training relevance, and show through a collection of experimental results that adding the suggested constraints significantly improves the quality of solutions obtained.

Acceleration techniques for optimization over trained neural network ensembles

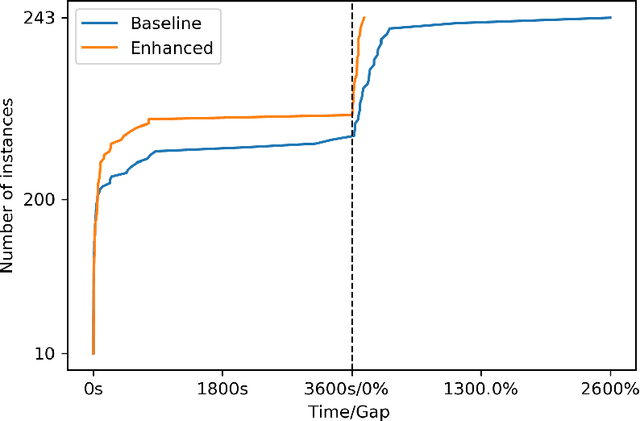
We study optimization problems where the objective function is modeled through feedforward neural networks with rectified linear unit (ReLU) activation. Recent literature has explored the use of a single neural network to model either uncertain or complex elements within an objective function. However, it is well known that ensembles of neural networks produce more stable predictions and have better generalizability than models with single neural networks, which suggests the application of ensembles of neural networks in a decision-making pipeline. We study how to incorporate a neural network ensemble as the objective function of an optimization model and explore computational approaches for the ensuing problem. We present a mixed-integer linear program based on existing popular big-$M$ formulations for optimizing over a single neural network. We develop two acceleration techniques for our model, the first one is a preprocessing procedure to tighten bounds for critical neurons in the neural network while the second one is a set of valid inequalities based on Benders decomposition. Experimental evaluations of our solution methods are conducted on one global optimization problem and two real-world data sets; the results suggest that our optimization algorithm outperforms the adaption of an state-of-the-art approach in terms of computational time and optimality gaps.

JANOS: An Integrated Predictive and Prescriptive Modeling Framework

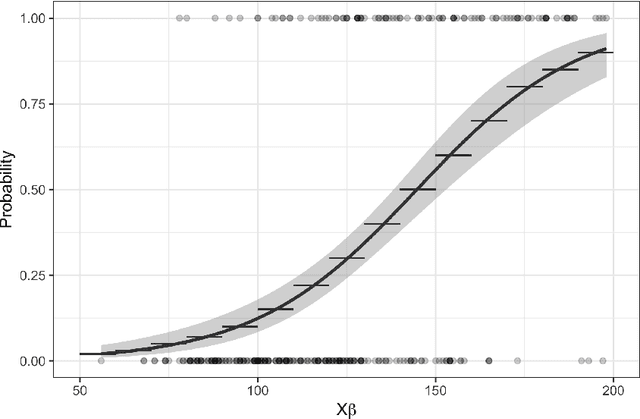
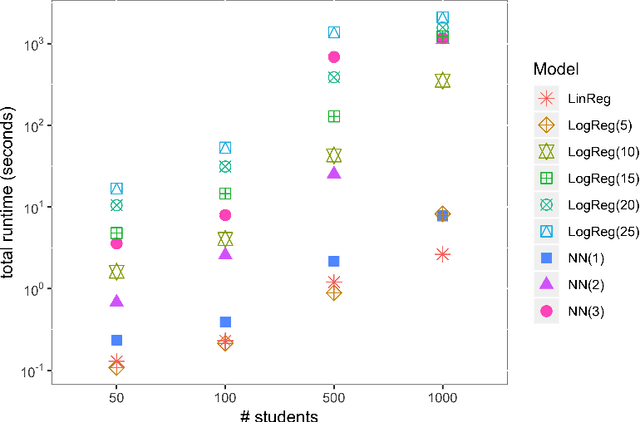
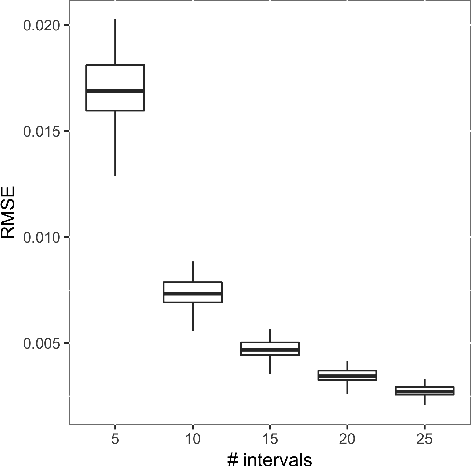
Business research practice is witnessing a surge in the integration of predictive modeling and prescriptive analysis. We describe a modeling framework JANOS that seamlessly integrates the two streams of analytics, for the first time allowing researchers and practitioners to embed machine learning models in an optimization framework. JANOS allows for specifying a prescriptive model using standard optimization modeling elements such as constraints and variables. The key novelty lies in providing modeling constructs that allow for the specification of commonly used predictive models and their features as constraints and variables in the optimization model. The framework considers two sets of decision variables; regular and predicted. The relationship between the regular and the predicted variables are specified by the user as pre-trained predictive models. JANOS currently supports linear regression, logistic regression, and neural network with rectified linear activation functions, but we plan to expand on this set in the future. In this paper, we demonstrate the flexibility of the framework through an example on scholarship allocation in a student enrollment problem and provide a numeric performance evaluation.

Improving Optimization Bounds using Machine Learning: Decision Diagrams meet Deep Reinforcement Learning

Finding tight bounds on the optimal solution is a critical element of practical solution methods for discrete optimization problems. In the last decade, decision diagrams (DDs) have brought a new perspective on obtaining upper and lower bounds that can be significantly better than classical bounding mechanisms, such as linear relaxations. It is well known that the quality of the bound achieved through this flexible bounding method is highly reliant on the ordering of variables chosen for building the diagram, and finding an ordering that optimizes standard metrics, or even improving one, is an NP-hard problem. In this paper, we propose an innovative and generic approach based on deep reinforcement learning for obtaining an ordering for tightening the bounds obtained with relaxed and restricted DDs. We apply the approach to both the Maximum Independent Set Problem and the Maximum Cut Problem. Experimental results on synthetic instances show that the deep reinforcement learning approach, by achieving tighter objective function bounds, generally outperforms ordering methods commonly used in the literature when the distribution of instances is known. To the best knowledge of the authors, this is the first paper to apply machine learning to directly improve relaxation bounds obtained by general-purpose bounding mechanisms for combinatorial optimization problems.