Careful! Training Relevance is Real

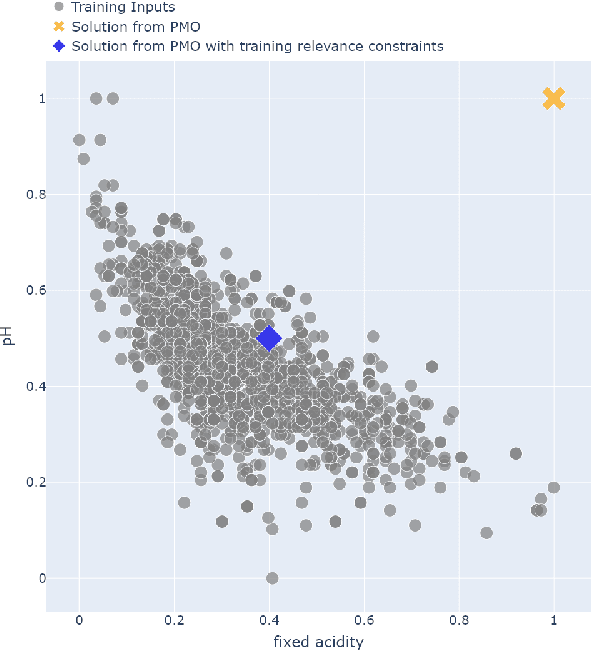
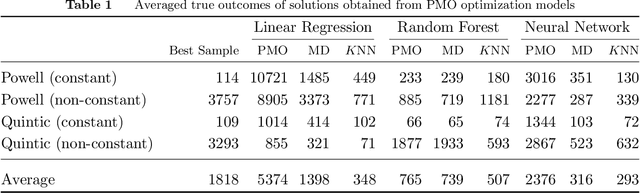
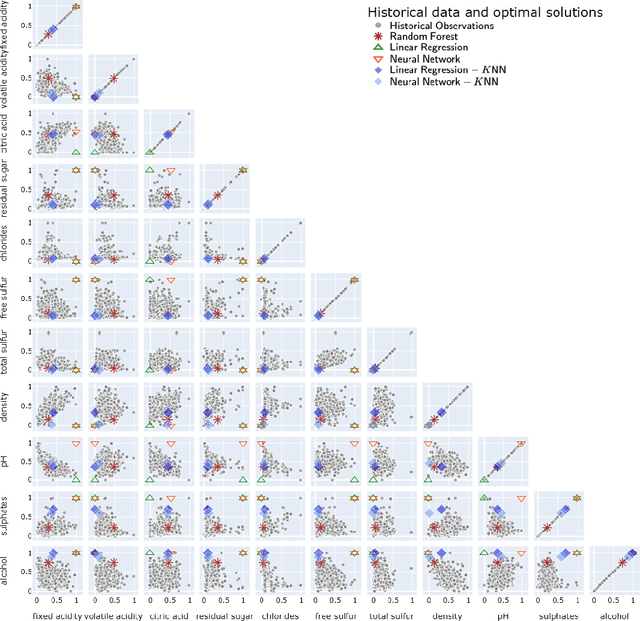
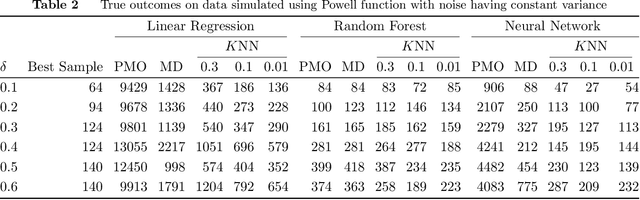
There is a recent proliferation of research on the integration of machine learning and optimization. One expansive area within this research stream is predictive-model embedded optimization, which uses pre-trained predictive models for the objective function of an optimization problem, so that features of the predictive models become decision variables in the optimization problem. Despite a recent surge in publications in this area, one aspect of this decision-making pipeline that has been largely overlooked is training relevance, i.e., ensuring that solutions to the optimization problem should be similar to the data used to train the predictive models. In this paper, we propose constraints designed to enforce training relevance, and show through a collection of experimental results that adding the suggested constraints significantly improves the quality of solutions obtained.

Acceleration techniques for optimization over trained neural network ensembles

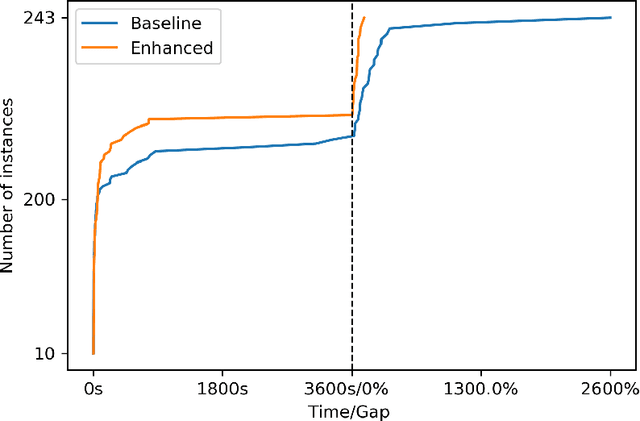
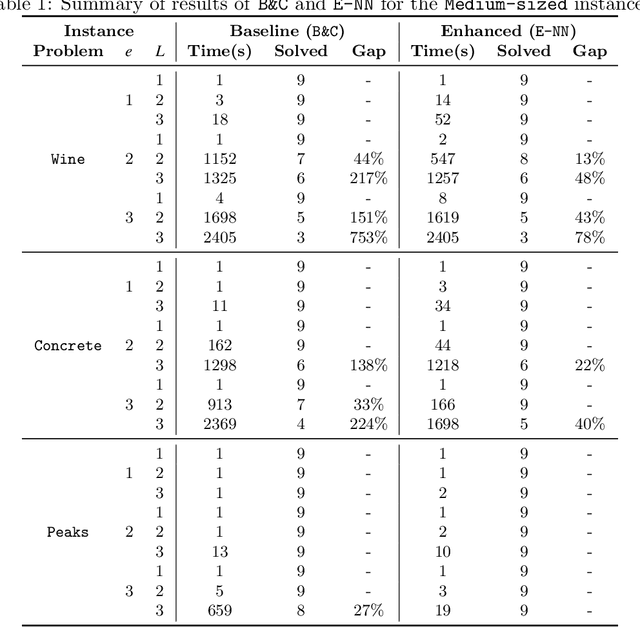
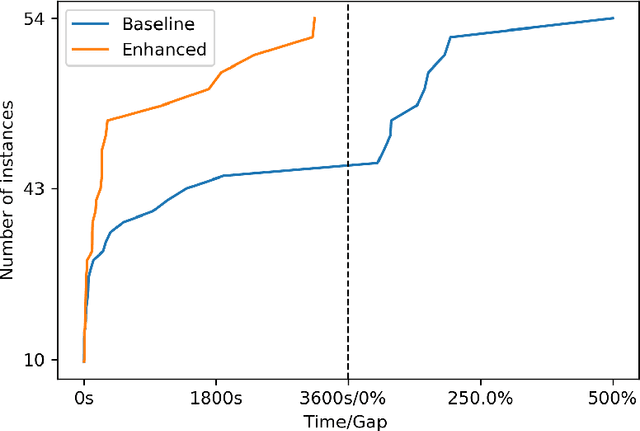
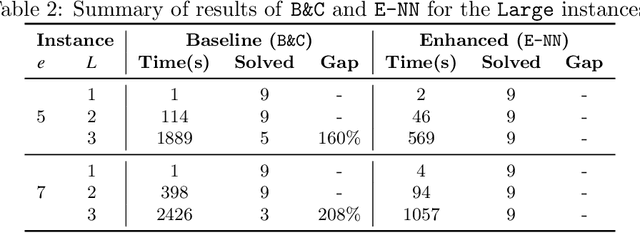
We study optimization problems where the objective function is modeled through feedforward neural networks with rectified linear unit (ReLU) activation. Recent literature has explored the use of a single neural network to model either uncertain or complex elements within an objective function. However, it is well known that ensembles of neural networks produce more stable predictions and have better generalizability than models with single neural networks, which suggests the application of ensembles of neural networks in a decision-making pipeline. We study how to incorporate a neural network ensemble as the objective function of an optimization model and explore computational approaches for the ensuing problem. We present a mixed-integer linear program based on existing popular big-$M$ formulations for optimizing over a single neural network. We develop two acceleration techniques for our model, the first one is a preprocessing procedure to tighten bounds for critical neurons in the neural network while the second one is a set of valid inequalities based on Benders decomposition. Experimental evaluations of our solution methods are conducted on one global optimization problem and two real-world data sets; the results suggest that our optimization algorithm outperforms the adaption of an state-of-the-art approach in terms of computational time and optimality gaps.