MORBDD: Multiobjective Restricted Binary Decision Diagrams by Learning to Sparsify

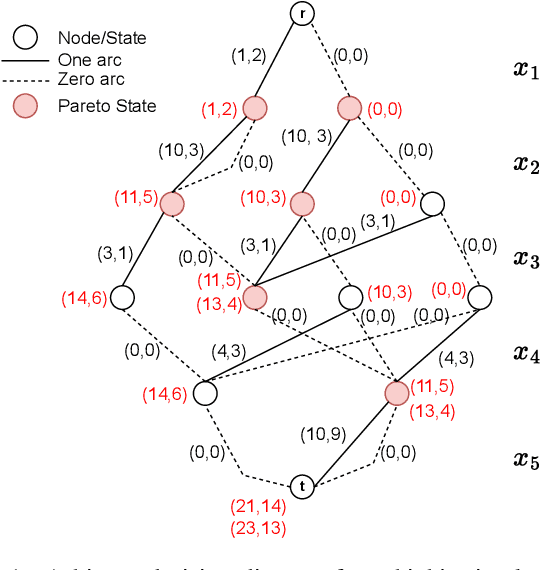
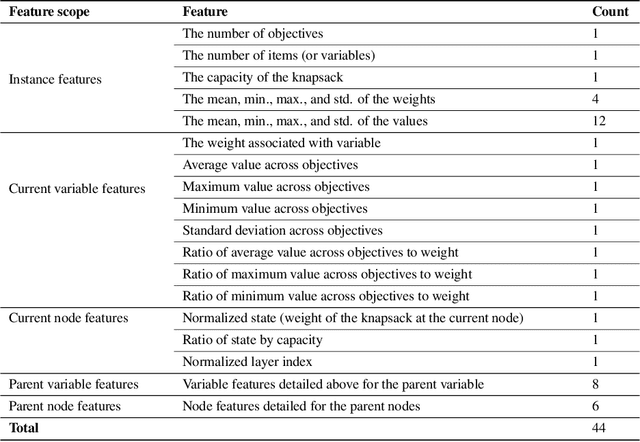
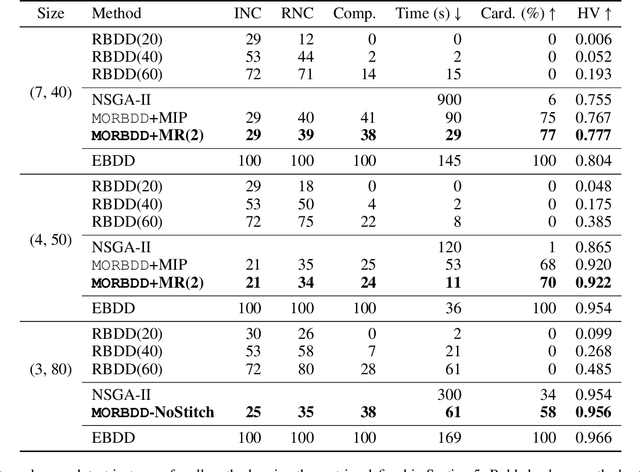
In multicriteria decision-making, a user seeks a set of non-dominated solutions to a (constrained) multiobjective optimization problem, the so-called Pareto frontier. In this work, we seek to bring a state-of-the-art method for exact multiobjective integer linear programming into the heuristic realm. We focus on binary decision diagrams (BDDs) which first construct a graph that represents all feasible solutions to the problem and then traverse the graph to extract the Pareto frontier. Because the Pareto frontier may be exponentially large, enumerating it over the BDD can be time-consuming. We explore how restricted BDDs, which have already been shown to be effective as heuristics for single-objective problems, can be adapted to multiobjective optimization through the use of machine learning (ML). MORBDD, our ML-based BDD sparsifier, first trains a binary classifier to eliminate BDD nodes that are unlikely to contribute to Pareto solutions, then post-processes the sparse BDD to ensure its connectivity via optimization. Experimental results on multiobjective knapsack problems show that MORBDD is highly effective at producing very small restricted BDDs with excellent approximation quality, outperforming width-limited restricted BDDs and the well-known evolutionary algorithm NSGA-II.

LEO: Learning Efficient Orderings for Multiobjective Binary Decision Diagrams

Approaches based on Binary decision diagrams (BDDs) have recently achieved state-of-the-art results for multiobjective integer programming problems. The variable ordering used in constructing BDDs can have a significant impact on their size and on the quality of bounds derived from relaxed or restricted BDDs for single-objective optimization problems. We first showcase a similar impact of variable ordering on the Pareto frontier (PF) enumeration time for the multiobjective knapsack problem, suggesting the need for deriving variable ordering methods that improve the scalability of the multiobjective BDD approach. To that end, we derive a novel parameter configuration space based on variable scoring functions which are linear in a small set of interpretable and easy-to-compute variable features. We show how the configuration space can be efficiently explored using black-box optimization, circumventing the curse of dimensionality (in the number of variables and objectives), and finding good orderings that reduce the PF enumeration time. However, black-box optimization approaches incur a computational overhead that outweighs the reduction in time due to good variable ordering. To alleviate this issue, we propose LEO, a supervised learning approach for finding efficient variable orderings that reduce the enumeration time. Experiments on benchmark sets from the knapsack problem with 3-7 objectives and up to 80 variables show that LEO is ~30-300% and ~10-200% faster at PF enumeration than common ordering strategies and algorithm configuration. Our code and instances are available at https://github.com/khalil-research/leo.

Neur2SP: Neural Two-Stage Stochastic Programming

Stochastic programming is a powerful modeling framework for decision-making under uncertainty. In this work, we tackle two-stage stochastic programs (2SPs), the most widely applied and studied class of stochastic programming models. Solving 2SPs exactly requires evaluation of an expected value function that is computationally intractable. Additionally, having a mixed-integer linear program (MIP) or a nonlinear program (NLP) in the second stage further aggravates the problem difficulty. In such cases, solving them can be prohibitively expensive even if specialized algorithms that exploit problem structure are employed. Finding high-quality (first-stage) solutions -- without leveraging problem structure -- can be crucial in such settings. We develop Neur2SP, a new method that approximates the expected value function via a neural network to obtain a surrogate model that can be solved more efficiently than the traditional extensive formulation approach. Moreover, Neur2SP makes no assumptions about the problem structure, in particular about the second-stage problem, and can be implemented using an off-the-shelf solver and open-source libraries. Our extensive computational experiments on benchmark 2SP datasets from four problem classes with different structures (containing MIP and NLP second-stage problems) show the efficiency (time) and efficacy (solution quality) of Neur2SP. Specifically, the proposed method takes less than 1.66 seconds across all problems, achieving high-quality solutions even as the number of scenarios increases, an ideal property that is difficult to have for traditional 2SP solution techniques. Namely, the most generic baseline method typically requires minutes to hours to find solutions of comparable quality.

A learning-based algorithm to quickly compute good primal solutions for Stochastic Integer Programs

We propose a novel approach using supervised learning to obtain near-optimal primal solutions for two-stage stochastic integer programming (2SIP) problems with constraints in the first and second stages. The goal of the algorithm is to predict a "representative scenario" (RS) for the problem such that, deterministically solving the 2SIP with the random realization equal to the RS, gives a near-optimal solution to the original 2SIP. Predicting an RS, instead of directly predicting a solution ensures first-stage feasibility of the solution. If the problem is known to have complete recourse, second-stage feasibility is also guaranteed. For computational testing, we learn to find an RS for a two-stage stochastic facility location problem with integer variables and linear constraints in both stages and consistently provide near-optimal solutions. Our computing times are very competitive with those of general-purpose integer programming solvers to achieve a similar solution quality.

Correlated discrete data generation using adversarial training

Generative Adversarial Networks (GAN) have shown great promise in tasks like synthetic image generation, image inpainting, style transfer, and anomaly detection. However, generating discrete data is a challenge. This work presents an adversarial training based correlated discrete data (CDD) generation model. It also details an approach for conditional CDD generation. The results of our approach are presented over two datasets; job-seeking candidates skill set (private dataset) and MNIST (public dataset). From quantitative and qualitative analysis of these results, we show that our model performs better as it leverages inherent correlation in the data, than an existing model that overlooks correlation.