Neur2BiLO: Neural Bilevel Optimization

Bilevel optimization deals with nested problems in which a leader takes the first decision to minimize their objective function while accounting for a follower's best-response reaction. Constrained bilevel problems with integer variables are particularly notorious for their hardness. While exact solvers have been proposed for mixed-integer linear bilevel optimization, they tend to scale poorly with problem size and are hard to generalize to the non-linear case. On the other hand, problem-specific algorithms (exact and heuristic) are limited in scope. Under a data-driven setting in which similar instances of a bilevel problem are solved routinely, our proposed framework, Neur2BiLO, embeds a neural network approximation of the leader's or follower's value function, trained via supervised regression, into an easy-to-solve mixed-integer program. Neur2BiLO serves as a heuristic that produces high-quality solutions extremely fast for the bilevel knapsack interdiction problem, the "critical node game" from network security, a donor-recipient healthcare problem, and discrete network design from transportation planning. These problems are diverse in that they have linear or non-linear objectives/constraints and integer or mixed-integer variables, making Neur2BiLO unique in its versatility.

Neur2RO: Neural Two-Stage Robust Optimization

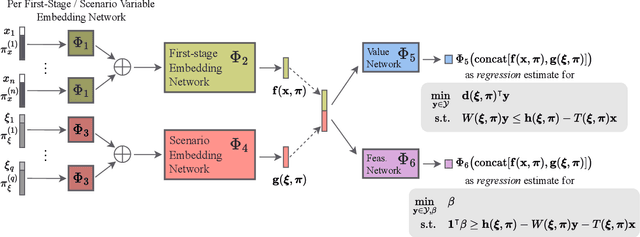
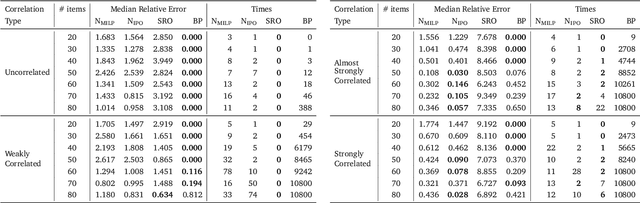
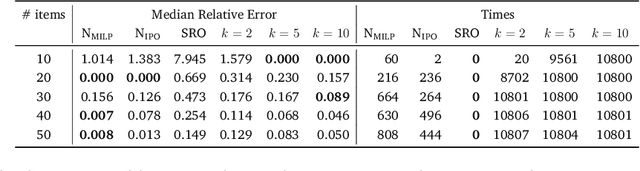
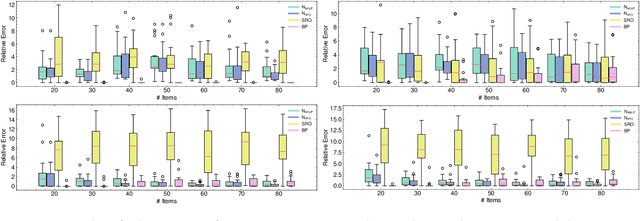
Robust optimization provides a mathematical framework for modeling and solving decision-making problems under worst-case uncertainty. This work addresses two-stage robust optimization (2RO) problems (also called adjustable robust optimization), wherein first-stage and second-stage decisions are made before and after uncertainty is realized, respectively. This results in a nested min-max-min optimization problem which is extremely challenging computationally, especially when the decisions are discrete. We propose Neur2RO, an efficient machine learning-driven instantiation of column-and-constraint generation (CCG), a classical iterative algorithm for 2RO. Specifically, we learn to estimate the value function of the second-stage problem via a novel neural network architecture that is easy to optimize over by design. Embedding our neural network into CCG yields high-quality solutions quickly as evidenced by experiments on two 2RO benchmarks, knapsack and capital budgeting. For knapsack, Neur2RO finds solutions that are within roughly $2\%$ of the best-known values in a few seconds compared to the three hours of the state-of-the-art exact branch-and-price algorithm; for larger and more complex instances, Neur2RO finds even better solutions. For capital budgeting, Neur2RO outperforms three variants of the $k$-adaptability algorithm, particularly on the largest instances, with a 5 to 10-fold reduction in solution time. Our code and data are available at https://github.com/khalil-research/Neur2RO.

Neur2SP: Neural Two-Stage Stochastic Programming

Stochastic programming is a powerful modeling framework for decision-making under uncertainty. In this work, we tackle two-stage stochastic programs (2SPs), the most widely applied and studied class of stochastic programming models. Solving 2SPs exactly requires evaluation of an expected value function that is computationally intractable. Additionally, having a mixed-integer linear program (MIP) or a nonlinear program (NLP) in the second stage further aggravates the problem difficulty. In such cases, solving them can be prohibitively expensive even if specialized algorithms that exploit problem structure are employed. Finding high-quality (first-stage) solutions -- without leveraging problem structure -- can be crucial in such settings. We develop Neur2SP, a new method that approximates the expected value function via a neural network to obtain a surrogate model that can be solved more efficiently than the traditional extensive formulation approach. Moreover, Neur2SP makes no assumptions about the problem structure, in particular about the second-stage problem, and can be implemented using an off-the-shelf solver and open-source libraries. Our extensive computational experiments on benchmark 2SP datasets from four problem classes with different structures (containing MIP and NLP second-stage problems) show the efficiency (time) and efficacy (solution quality) of Neur2SP. Specifically, the proposed method takes less than 1.66 seconds across all problems, achieving high-quality solutions even as the number of scenarios increases, an ideal property that is difficult to have for traditional 2SP solution techniques. Namely, the most generic baseline method typically requires minutes to hours to find solutions of comparable quality.

The Machine Learning for Combinatorial Optimization Competition (ML4CO): Results and Insights

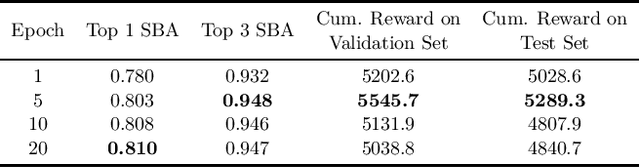
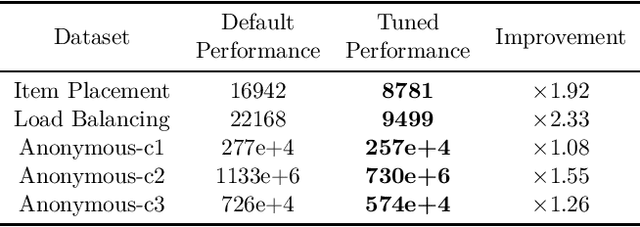
Combinatorial optimization is a well-established area in operations research and computer science. Until recently, its methods have focused on solving problem instances in isolation, ignoring that they often stem from related data distributions in practice. However, recent years have seen a surge of interest in using machine learning as a new approach for solving combinatorial problems, either directly as solvers or by enhancing exact solvers. Based on this context, the ML4CO aims at improving state-of-the-art combinatorial optimization solvers by replacing key heuristic components. The competition featured three challenging tasks: finding the best feasible solution, producing the tightest optimality certificate, and giving an appropriate solver configuration. Three realistic datasets were considered: balanced item placement, workload apportionment, and maritime inventory routing. This last dataset was kept anonymous for the contestants.

Ecole: A Library for Learning Inside MILP Solvers

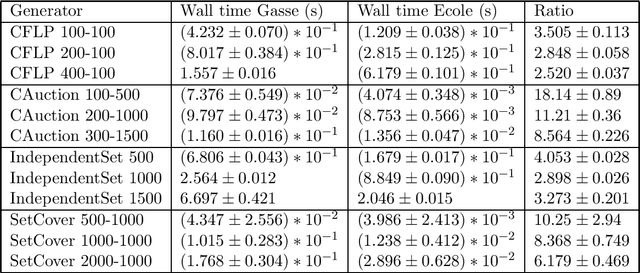
In this paper we describe Ecole (Extensible Combinatorial Optimization Learning Environments), a library to facilitate integration of machine learning in combinatorial optimization solvers. It exposes sequential decision making that must be performed in the process of solving as Markov decision processes. This means that, rather than trying to predict solutions to combinatorial optimization problems directly, Ecole allows machine learning to work in cooperation with a state-of-the-art a mixed-integer linear programming solver that acts as a controllable algorithm. Ecole provides a collection of computationally efficient, ready to use learning environments, which are also easy to extend to define novel training tasks. Documentation and code can be found at https://www.ecole.ai.

Can Machine Learning Help in Solving Cargo Capacity Management Booking Control Problems?

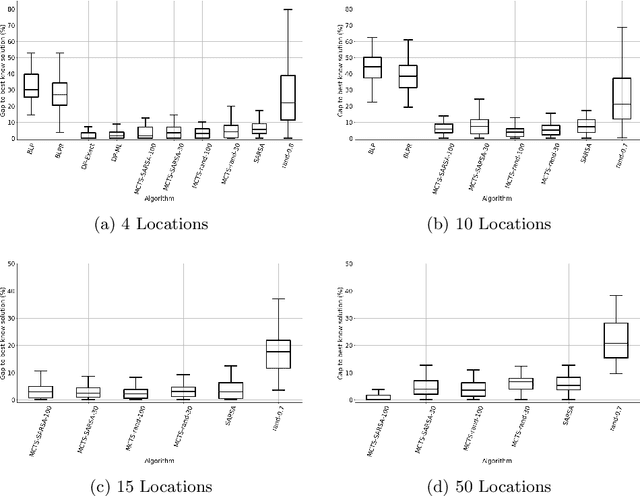
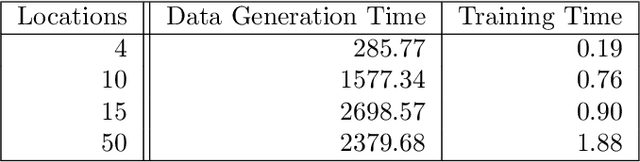
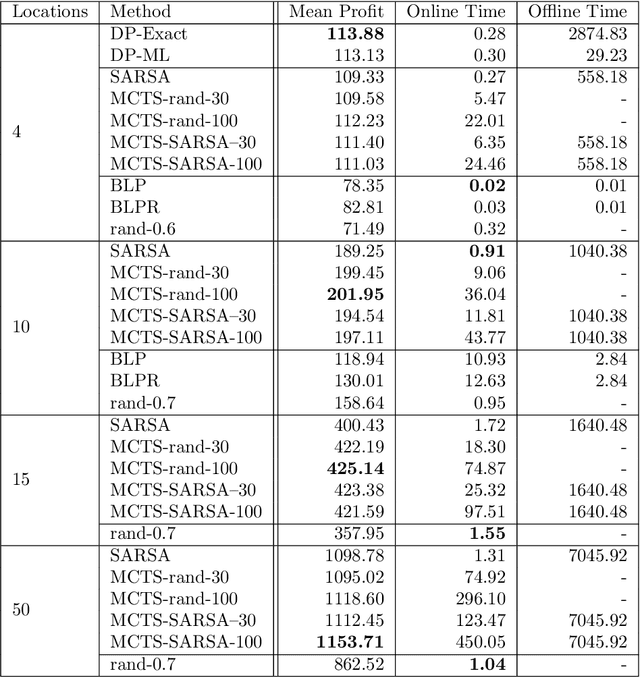
Revenue management is important for carriers (e.g., airlines and railroads). In this paper, we focus on cargo capacity management which has received less attention in the literature than its passenger counterpart. More precisely, we focus on the problem of controlling booking accept/reject decisions: Given a limited capacity, accept a booking request or reject it to reserve capacity for future bookings with potentially higher revenue. We formulate the problem as a finite-horizon stochastic dynamic program. The cost of fulfilling the accepted bookings, incurred at the end of the horizon, depends on the packing and routing of the cargo. This is a computationally challenging aspect as the latter are solutions to an operational decision-making problem, in our application a vehicle routing problem (VRP). Seeking a balance between online and offline computation, we propose to train a predictor of the solution costs to the VRPs using supervised learning. In turn, we use the predictions online in approximate dynamic programming and reinforcement learning algorithms to solve the booking control problem. We compare the results to an existing approach in the literature and show that we are able to obtain control policies that provide increased profit at a reduced evaluation time. This is achieved thanks to accurate approximation of the operational costs and negligible computing time in comparison to solving the VRPs.

Ecole: A Gym-like Library for Machine Learning in Combinatorial Optimization Solvers

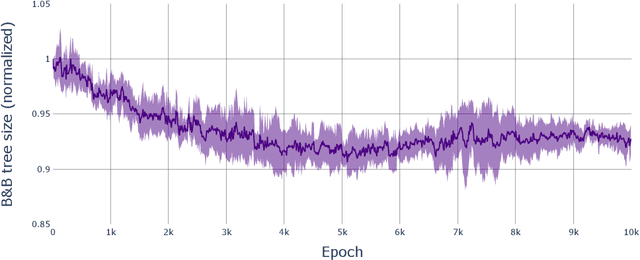
We present Ecole, a new library to simplify machine learning research for combinatorial optimization. Ecole exposes several key decision tasks arising in general-purpose combinatorial optimization solvers as control problems over Markov decision processes. Its interface mimics the popular OpenAI Gym library and is both extensible and intuitive to use. We aim at making this library a standardized platform that will lower the bar of entry and accelerate innovation in the field. Documentation and code can be found at https://www.ecole.ai.