Decoupling regularization from the action space

Regularized reinforcement learning (RL), particularly the entropy-regularized kind, has gained traction in optimal control and inverse RL. While standard unregularized RL methods remain unaffected by changes in the number of actions, we show that it can severely impact their regularized counterparts. This paper demonstrates the importance of decoupling the regularizer from the action space: that is, to maintain a consistent level of regularization regardless of how many actions are involved to avoid over-regularization. Whereas the problem can be avoided by introducing a task-specific temperature parameter, it is often undesirable and cannot solve the problem when action spaces are state-dependent. In the state-dependent action context, different states with varying action spaces are regularized inconsistently. We introduce two solutions: a static temperature selection approach and a dynamic counterpart, universally applicable where this problem arises. Implementing these changes improves performance on the DeepMind control suite in static and dynamic temperature regimes and a biological sequence design task.

Maximum entropy GFlowNets with soft Q-learning

Generative Flow Networks (GFNs) have emerged as a powerful tool for sampling discrete objects from unnormalized distributions, offering a scalable alternative to Markov Chain Monte Carlo (MCMC) methods. While GFNs draw inspiration from maximum entropy reinforcement learning (RL), the connection between the two has largely been unclear and seemingly applicable only in specific cases. This paper addresses the connection by constructing an appropriate reward function, thereby establishing an exact relationship between GFNs and maximum entropy RL. This construction allows us to introduce maximum entropy GFNs, which, in contrast to GFNs with uniform backward policy, achieve the maximum entropy attainable by GFNs without constraints on the state space.

A Survey of Contextual Optimization Methods for Decision Making under Uncertainty

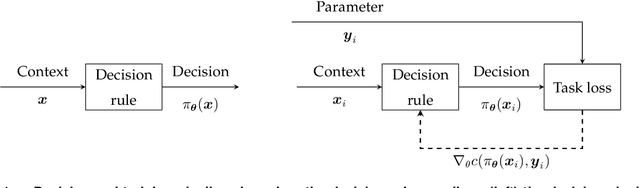
Recently there has been a surge of interest in operations research (OR) and the machine learning (ML) community in combining prediction algorithms and optimization techniques to solve decision-making problems in the face of uncertainty. This gave rise to the field of contextual optimization, under which data-driven procedures are developed to prescribe actions to the decision-maker that make the best use of the most recently updated information. A large variety of models and methods have been presented in both OR and ML literature under a variety of names, including data-driven optimization, prescriptive optimization, predictive stochastic programming, policy optimization, (smart) predict/estimate-then-optimize, decision-focused learning, (task-based) end-to-end learning/forecasting/optimization, etc. Focusing on single and two-stage stochastic programming problems, this review article identifies three main frameworks for learning policies from data and discusses their strengths and limitations. We present the existing models and methods under a uniform notation and terminology and classify them according to the three main frameworks identified. Our objective with this survey is to both strengthen the general understanding of this active field of research and stimulate further theoretical and algorithmic advancements in integrating ML and stochastic programming.

Scope Restriction for Scalable Real-Time Railway Rescheduling: An Exploratory Study

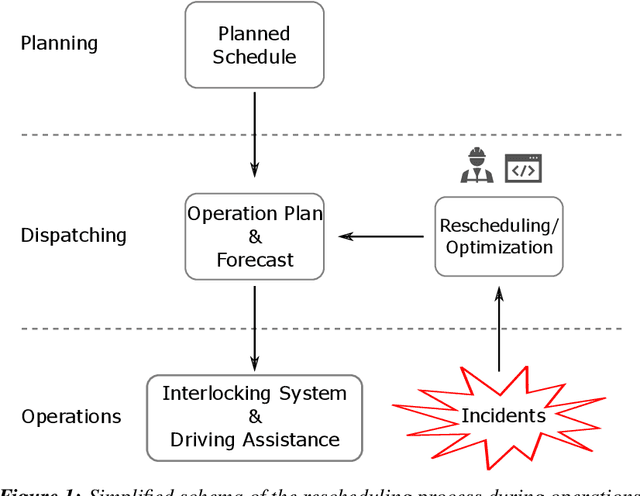
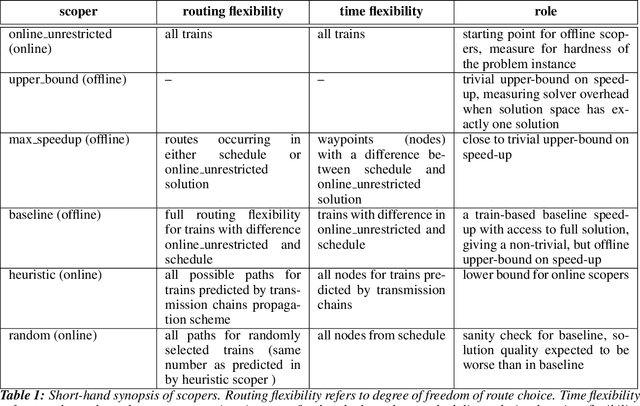
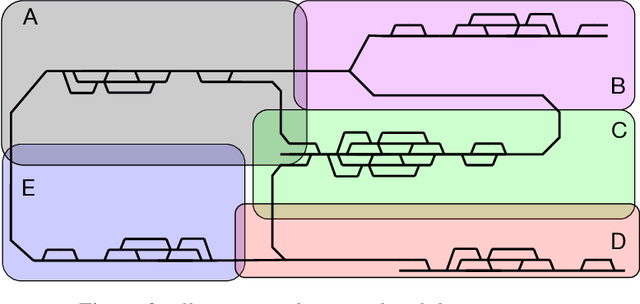
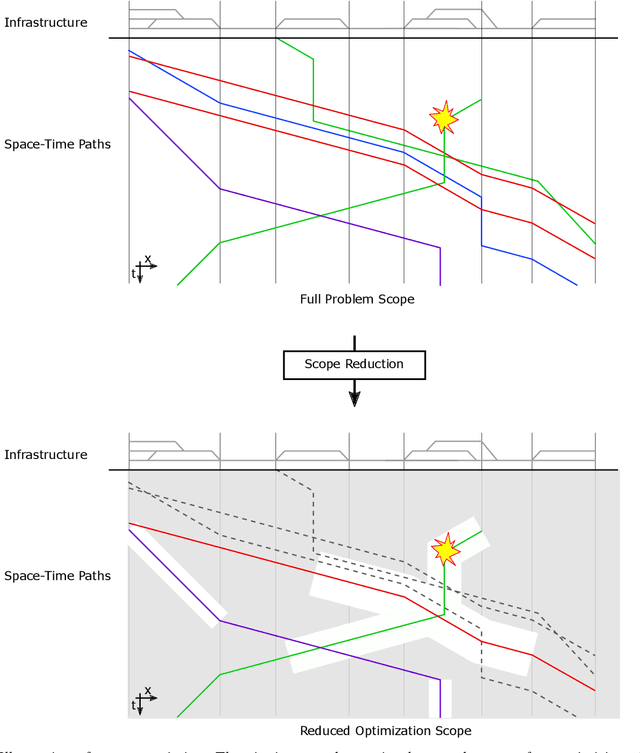
With the aim to stimulate future research, we describe an exploratory study of a railway rescheduling problem. A widely used approach in practice and state of the art is to decompose these complex problems by geographical scope. Instead, we propose defining a core problem that restricts a rescheduling problem in response to a disturbance to only trains that need to be rescheduled, hence restricting the scope in both time and space. In this context, the difficulty resides in defining a scoper that can predict a subset of train services that will be affected by a given disturbance. We report preliminary results using the Flatland simulation environment that highlights the potential and challenges of this idea. We provide an extensible playground open-source implementation based on the Flatland railway environment and Answer-Set Programming.

Arc travel time and path choice model estimation subsumed

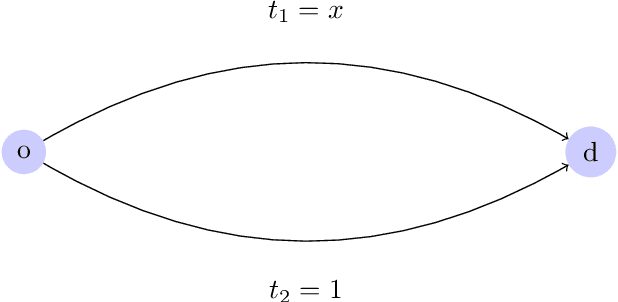
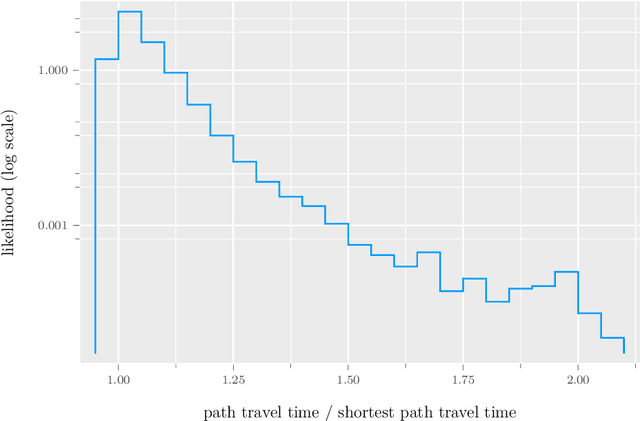
We propose a method for maximum likelihood estimation of path choice model parameters and arc travel time using data of different levels of granularity. Hitherto these two tasks have been tackled separately under strong assumptions. Using a small example, we illustrate that this can lead to biased results. Results on both real (New York yellow cab) and simulated data show strong performance of our method compared to existing baselines.

Fast Continuous and Integer L-shaped Heuristics Through Supervised Learning

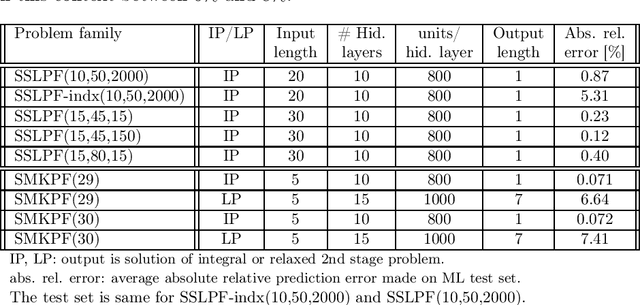
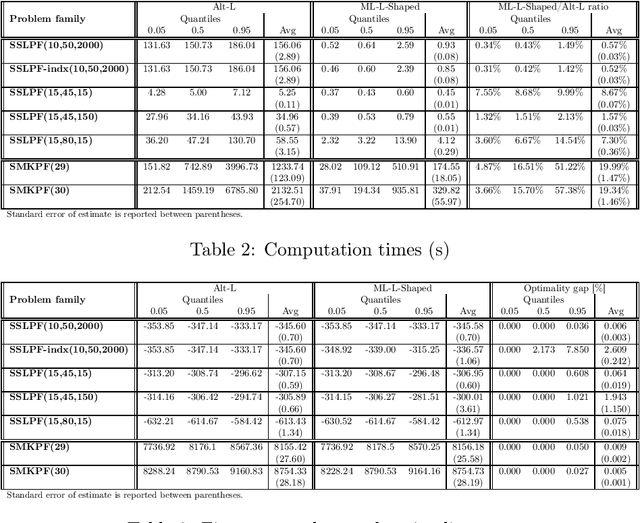
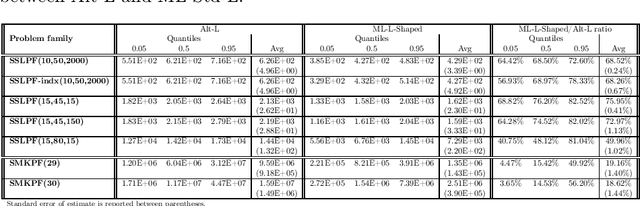
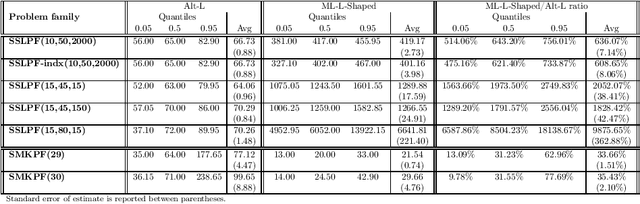
We propose a methodology at the nexus of operations research and machine learning (ML) leveraging generic approximators available from ML to accelerate the solution of mixed-integer linear two-stage stochastic programs. We aim at solving problems where the second stage is highly demanding. Our core idea is to gain large reductions in online solution time while incurring small reductions in first-stage solution accuracy by substituting the exact second-stage solutions with fast, yet accurate supervised ML predictions. This upfront investment in ML would be justified when similar problems are solved repeatedly over time, for example, in transport planning related to fleet management, routing and container yard management. Our numerical results focus on the problem class seminally addressed with the integer and continuous L-shaped cuts. Our extensive empirical analysis is grounded in standardized families of problems derived from stochastic server location (SSLP) and stochastic multi knapsack (SMKP) problems available in the literature. The proposed method can solve the hardest instances of SSLP in less than 9% of the time it takes the state-of-the-art exact method, and in the case of SMKP the same figure is 20%. Average optimality gaps are in most cases less than 0.1%.

Minimizing Entropy to Discover Good Solutions to Recurrent Mixed Integer Programs

Current state-of-the-art solvers for mixed-integer programming (MIP) problems are designed to perform well on a wide range of problems. However, for many real-world use cases, problem instances come from a narrow distribution. This has motivated the development of specialized methods that can exploit the information in historical datasets to guide the design of heuristics. Recent works have shown that machine learning (ML) can be integrated with an MIP solver to inject domain knowledge and efficiently close the optimality gap. This hybridization is usually done with deep learning (DL), which requires a large dataset and extensive hyperparameter tuning to perform well. This paper proposes an online heuristic that uses the notion of entropy to efficiently build a model with minimal training data and tuning. We test our method on the locomotive assignment problem (LAP), a recurring real-world problem that is challenging to solve at scale. Experimental results show a speed up of an order of magnitude compared to a general purpose solver (CPLEX) with a relative gap of less than 2%. We also observe that for some instances our method can discover better solutions than CPLEX within the time limit.

Periodic Freight Demand Forecasting for Large-scale Tactical Planning

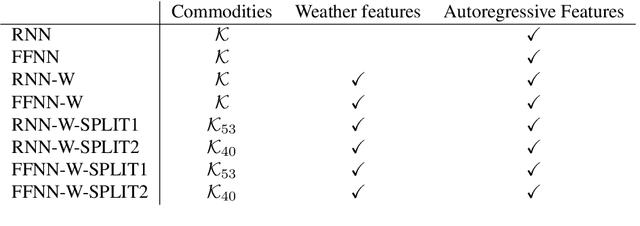
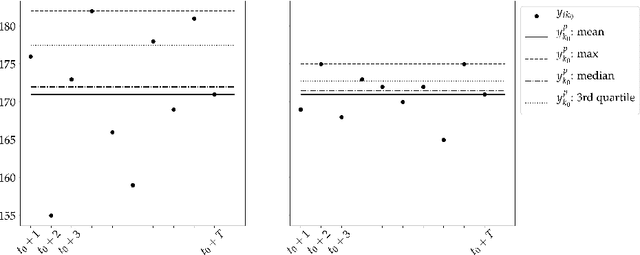
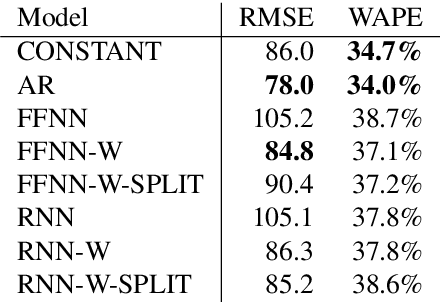
Crucial to freight carriers is the tactical planning of the service network. The aim is to obtain a cyclic plan over a given tactical planning horizon that satisfies predicted demand at a minimum cost. A central input to the planning process is the periodic demand, that is, the demand expected to repeat in every period in the planning horizon. We focus on large-scale tactical planning problems that require deterministic models for computational tractability. The problem of estimating periodic demand in this setting broadly present in practice has hitherto been overlooked in the literature. We address this gap by formally introducing the periodic demand estimation problem and propose a two-step methodology: Based on time series forecasts obtained in the first step, we propose, in the second step, to solve a multilevel mathematical programming formulation whose solution is a periodic demand estimate that minimizes fixed costs, and variable costs incurred by adapting the tactical plan at an operational level. We report results in an extensive empirical study of a real large-scale application from the Canadian National Railway Company. We compare our periodic demand estimates to the approach commonly used in practice which simply consists in using the mean of the time series forecasts. The results clearly show the importance of the periodic demand estimation problem. Indeed, the planning costs exhibit an important variation over different periodic demand estimates, and using an estimate different from the mean forecast can lead to substantial cost reductions. For example, the costs associated with the period demand estimates based on forecasts were comparable to, or even better than those obtained using the mean of actual demand.

Can Machine Learning Help in Solving Cargo Capacity Management Booking Control Problems?

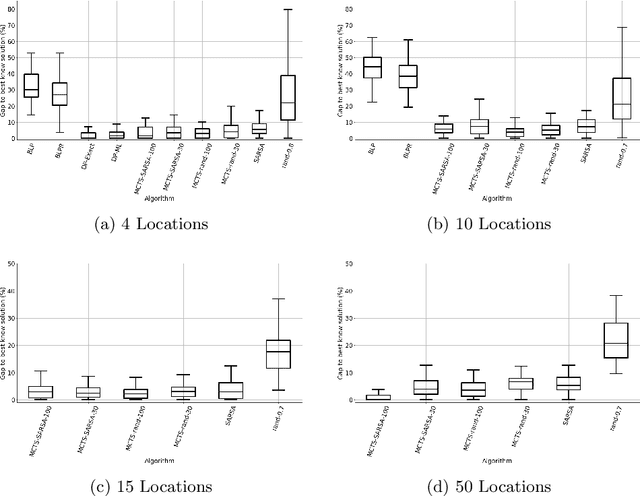
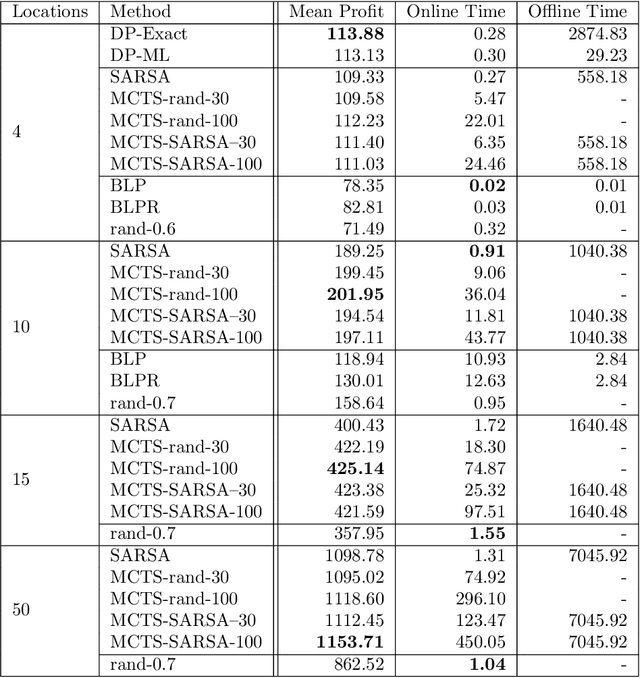
Revenue management is important for carriers (e.g., airlines and railroads). In this paper, we focus on cargo capacity management which has received less attention in the literature than its passenger counterpart. More precisely, we focus on the problem of controlling booking accept/reject decisions: Given a limited capacity, accept a booking request or reject it to reserve capacity for future bookings with potentially higher revenue. We formulate the problem as a finite-horizon stochastic dynamic program. The cost of fulfilling the accepted bookings, incurred at the end of the horizon, depends on the packing and routing of the cargo. This is a computationally challenging aspect as the latter are solutions to an operational decision-making problem, in our application a vehicle routing problem (VRP). Seeking a balance between online and offline computation, we propose to train a predictor of the solution costs to the VRPs using supervised learning. In turn, we use the predictions online in approximate dynamic programming and reinforcement learning algorithms to solve the booking control problem. We compare the results to an existing approach in the literature and show that we are able to obtain control policies that provide increased profit at a reduced evaluation time. This is achieved thanks to accurate approximation of the operational costs and negligible computing time in comparison to solving the VRPs.

Estimating the Impact of an Improvement to a Revenue Management System: An Airline Application

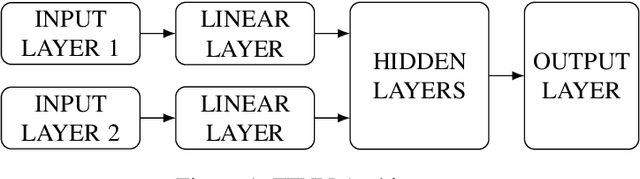
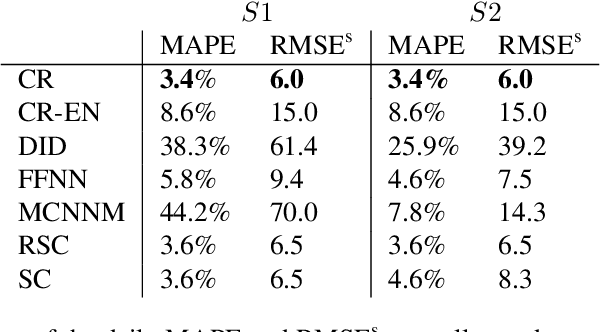
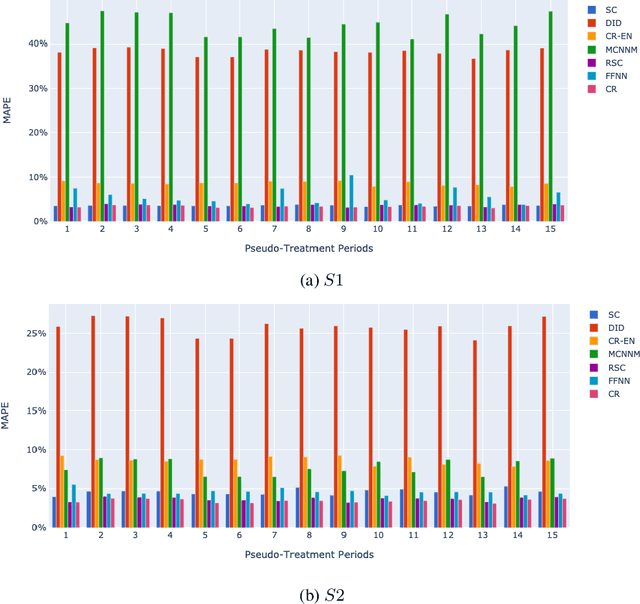
Airlines have been making use of highly complex Revenue Management Systems to maximize revenue for decades. Estimating the impact of changing one component of those systems on an important outcome such as revenue is crucial, yet very challenging. It is indeed the difference between the generated value and the value that would have been generated keeping business as usual, which is not observable. We provide a comprehensive overview of counterfactual prediction models and use them in an extensive computational study based on data from Air Canada to estimate such impact. We focus on predicting the counterfactual revenue and compare it to the observed revenue subject to the impact. Our microeconomic application and small expected treatment impact stand out from the usual synthetic control applications. We present accurate linear and deep-learning counterfactual prediction models which achieve respectively 1.1% and 1% of error and allow to estimate a simulated effect quite accurately.