Eric Larsen
Fast Continuous and Integer L-shaped Heuristics Through Supervised Learning
May 02, 2022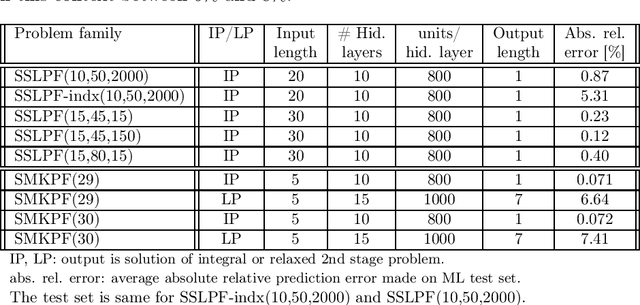
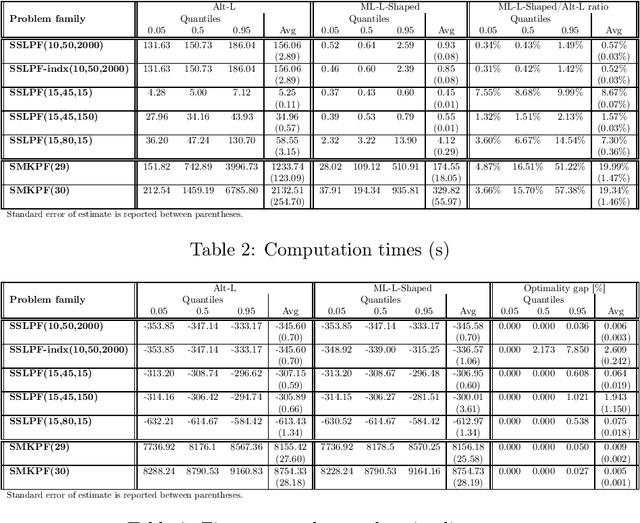
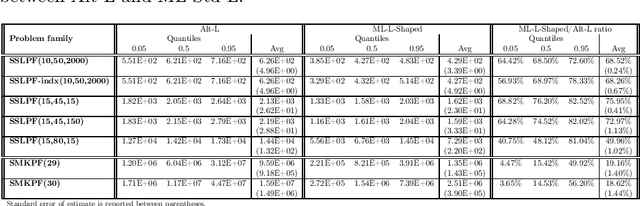
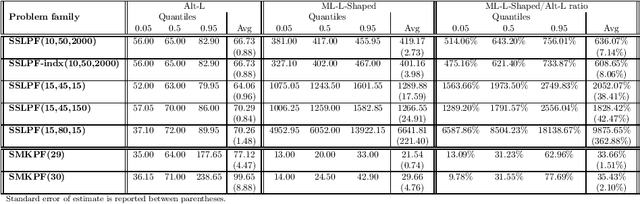
Abstract:We propose a methodology at the nexus of operations research and machine learning (ML) leveraging generic approximators available from ML to accelerate the solution of mixed-integer linear two-stage stochastic programs. We aim at solving problems where the second stage is highly demanding. Our core idea is to gain large reductions in online solution time while incurring small reductions in first-stage solution accuracy by substituting the exact second-stage solutions with fast, yet accurate supervised ML predictions. This upfront investment in ML would be justified when similar problems are solved repeatedly over time, for example, in transport planning related to fleet management, routing and container yard management. Our numerical results focus on the problem class seminally addressed with the integer and continuous L-shaped cuts. Our extensive empirical analysis is grounded in standardized families of problems derived from stochastic server location (SSLP) and stochastic multi knapsack (SMKP) problems available in the literature. The proposed method can solve the hardest instances of SSLP in less than 9% of the time it takes the state-of-the-art exact method, and in the case of SMKP the same figure is 20%. Average optimality gaps are in most cases less than 0.1%.
A language processing algorithm for predicting tactical solutions to an operational planning problem under uncertainty
Oct 18, 2019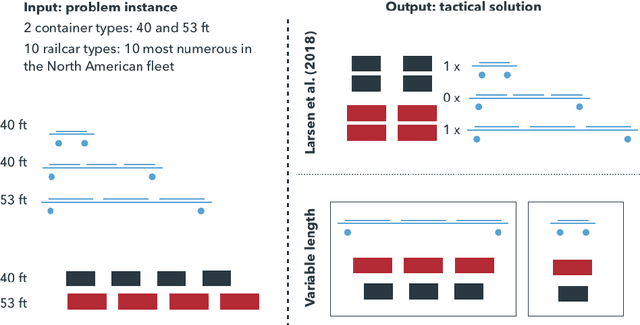

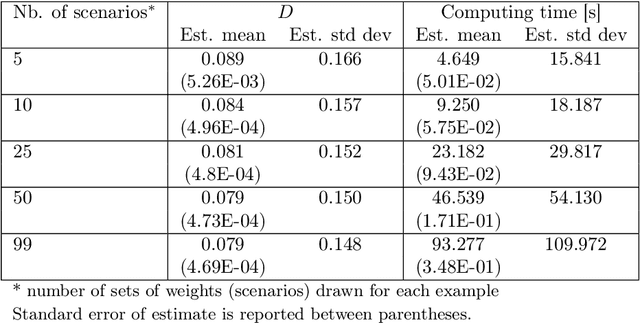
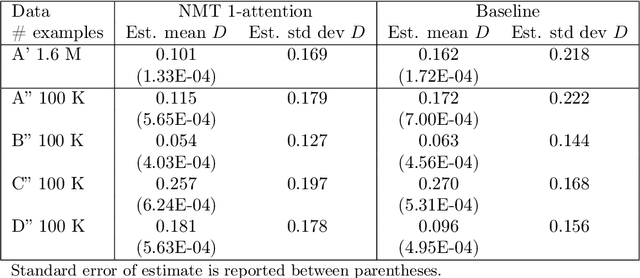
Abstract:This paper is devoted to the prediction of solutions to a stochastic discrete optimization problem. Through an application, we illustrate how we can use a state-of-the-art neural machine translation (NMT) algorithm to predict the solutions by defining appropriate vocabularies, syntaxes and constraints. We attend to applications where the predictions need to be computed in very short computing time -- in the order of milliseconds or less. The results show that with minimal adaptations to the model architecture and hyperparameter tuning, the NMT algorithm can produce accurate solutions within the computing time budget. While these predictions are slightly less accurate than approximate stochastic programming solutions (sample average approximation), they can be computed faster and with less variability.
Predicting Tactical Solutions to Operational Planning Problems under Imperfect Information
Jan 22, 2019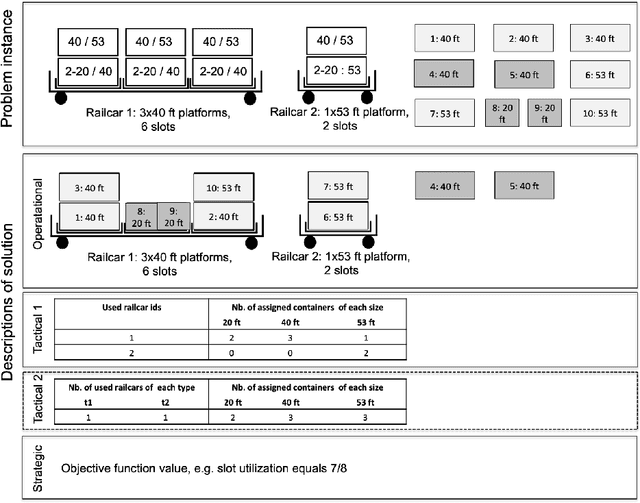

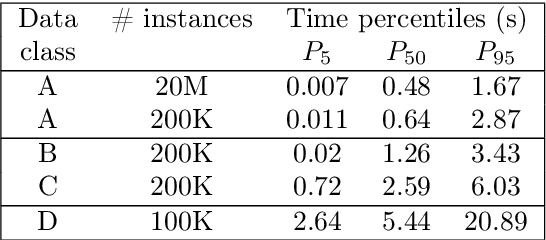
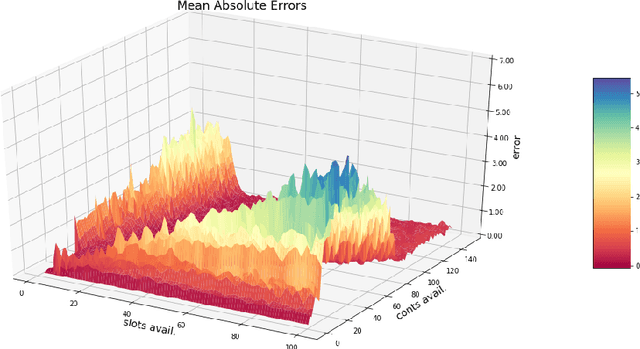
Abstract:This paper offers a methodological contribution at the intersection of machine learning and operations research. Namely, we propose a methodology to quickly predict tactical solutions to a given operational problem. In this context, the tactical solution is less detailed than the operational one but it has to be computed in very short time and under imperfect information. The problem is of importance in various applications where tactical and operational planning problems are interrelated and information about the operational problem is revealed over time. This is for instance the case in certain capacity planning and demand management systems. We formulate the problem as a two-stage optimal prediction stochastic program whose solution we predict with a supervised machine learning algorithm. The training data set consists of a large number of deterministic (second stage) problems generated by controlled probabilistic sampling. The labels are computed based on solutions to the deterministic problems (solved independently and offline) employing appropriate aggregation and subselection methods to address uncertainty. Results on our motivating application in load planning for rail transportation show that deep learning algorithms produce highly accurate predictions in very short computing time (milliseconds or less). The prediction accuracy is comparable to solutions computed by sample average approximation of the stochastic program.
Predicting Solution Summaries to Integer Linear Programs under Imperfect Information with Machine Learning
Sep 12, 2018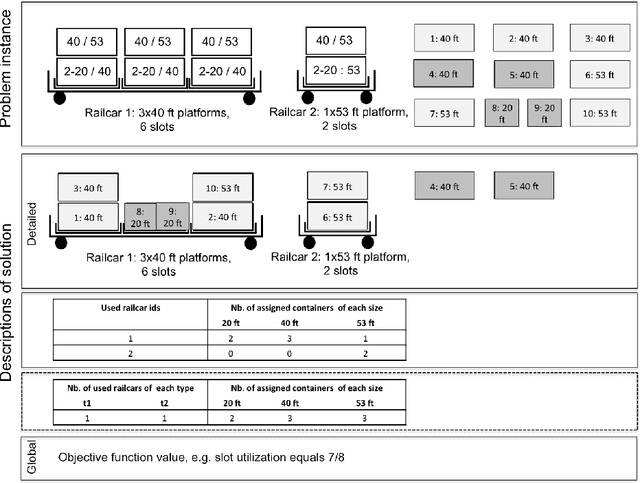
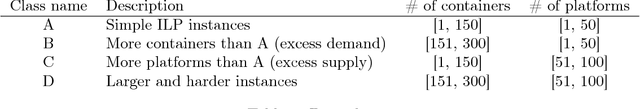
Abstract:The paper provides a methodological contribution at the intersection of machine learning and operations research. Namely, we propose a methodology to quickly predict solution summaries (i.e., solution descriptions at a given level of detail) to discrete stochastic optimization problems. We approximate the solutions based on supervised learning and the training dataset consists of a large number of deterministic problems that have been solved independently and offline. Uncertainty regarding a missing subset of the inputs is addressed through sampling and aggregation methods. Our motivating application concerns booking decisions of intermodal containers on double-stack trains. Under perfect information, this is the so-called load planning problem and it can be formulated by means of integer linear programming. However, the formulation cannot be used for the application at hand because of the restricted computational budget and unknown container weights. The results show that standard deep learning algorithms allow one to predict descriptions of solutions with high accuracy in very short time (milliseconds or less).
Theano: A Python framework for fast computation of mathematical expressions
May 09, 2016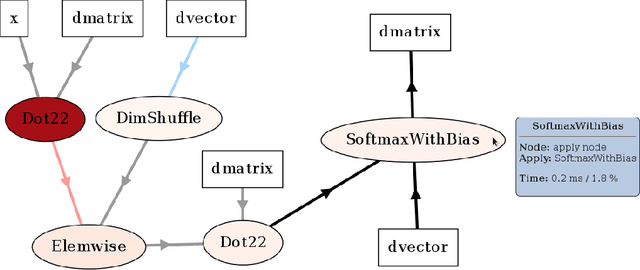
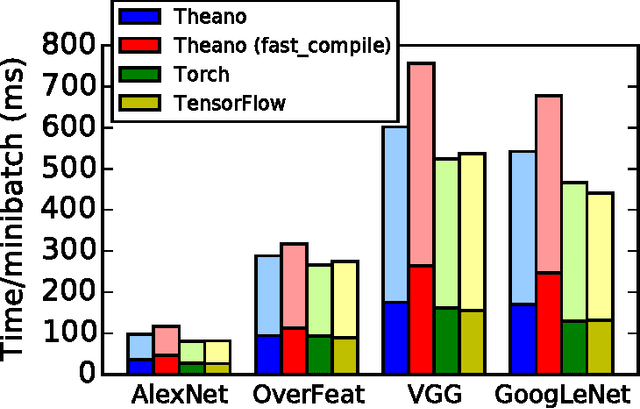
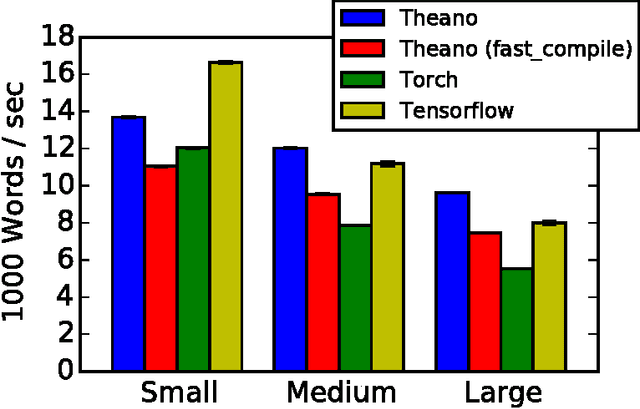
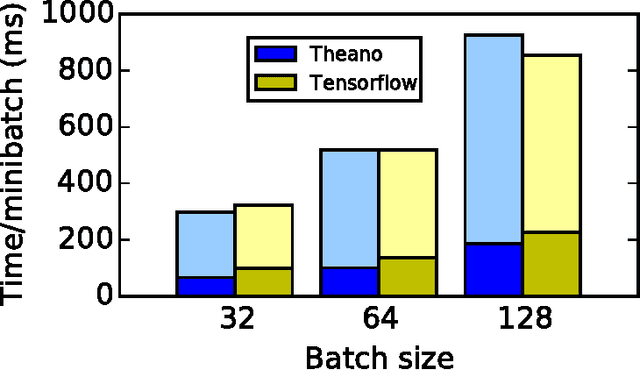
Abstract:Theano is a Python library that allows to define, optimize, and evaluate mathematical expressions involving multi-dimensional arrays efficiently. Since its introduction, it has been one of the most used CPU and GPU mathematical compilers - especially in the machine learning community - and has shown steady performance improvements. Theano is being actively and continuously developed since 2008, multiple frameworks have been built on top of it and it has been used to produce many state-of-the-art machine learning models. The present article is structured as follows. Section I provides an overview of the Theano software and its community. Section II presents the principal features of Theano and how to use them, and compares them with other similar projects. Section III focuses on recently-introduced functionalities and improvements. Section IV compares the performance of Theano against Torch7 and TensorFlow on several machine learning models. Section V discusses current limitations of Theano and potential ways of improving it.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge