Periodic Freight Demand Forecasting for Large-scale Tactical Planning
Paper and Code
May 19, 2021
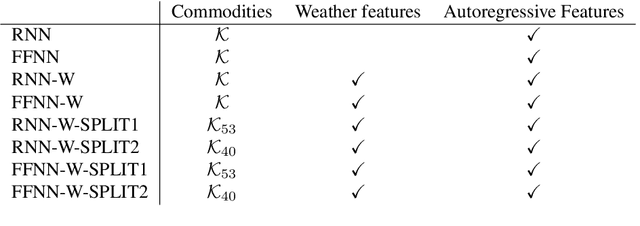
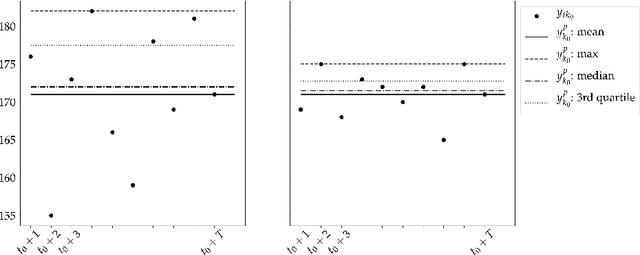
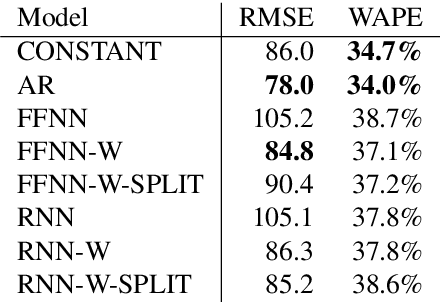
Crucial to freight carriers is the tactical planning of the service network. The aim is to obtain a cyclic plan over a given tactical planning horizon that satisfies predicted demand at a minimum cost. A central input to the planning process is the periodic demand, that is, the demand expected to repeat in every period in the planning horizon. We focus on large-scale tactical planning problems that require deterministic models for computational tractability. The problem of estimating periodic demand in this setting broadly present in practice has hitherto been overlooked in the literature. We address this gap by formally introducing the periodic demand estimation problem and propose a two-step methodology: Based on time series forecasts obtained in the first step, we propose, in the second step, to solve a multilevel mathematical programming formulation whose solution is a periodic demand estimate that minimizes fixed costs, and variable costs incurred by adapting the tactical plan at an operational level. We report results in an extensive empirical study of a real large-scale application from the Canadian National Railway Company. We compare our periodic demand estimates to the approach commonly used in practice which simply consists in using the mean of the time series forecasts. The results clearly show the importance of the periodic demand estimation problem. Indeed, the planning costs exhibit an important variation over different periodic demand estimates, and using an estimate different from the mean forecast can lead to substantial cost reductions. For example, the costs associated with the period demand estimates based on forecasts were comparable to, or even better than those obtained using the mean of actual demand.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge