PySCIPOpt-ML: Embedding Trained Machine Learning Models into Mixed-Integer Programs

A standard tool for modelling real-world optimisation problems is mixed-integer programming (MIP). However, for many of these problems there is either incomplete information describing variable relations, or the relations between variables are highly complex. To overcome both these hurdles, machine learning (ML) models are often used and embedded in the MIP as surrogate models to represent these relations. Due to the large amount of available ML frameworks, formulating ML models into MIPs is highly non-trivial. In this paper we propose a tool for the automatic MIP formulation of trained ML models, allowing easy integration of ML constraints into MIPs. In addition, we introduce a library of MIP instances with embedded ML constraints. The project is available at https://github.com/Opt-Mucca/PySCIPOpt-ML.

Online Learning for Scheduling MIP Heuristics

Mixed Integer Programming (MIP) is NP-hard, and yet modern solvers often solve large real-world problems within minutes. This success can partially be attributed to heuristics. Since their behavior is highly instance-dependent, relying on hard-coded rules derived from empirical testing on a large heterogeneous corpora of benchmark instances might lead to sub-optimal performance. In this work, we propose an online learning approach that adapts the application of heuristics towards the single instance at hand. We replace the commonly used static heuristic handling with an adaptive framework exploiting past observations about the heuristic's behavior to make future decisions. In particular, we model the problem of controlling Large Neighborhood Search and Diving - two broad and complex classes of heuristics - as a multi-armed bandit problem. Going beyond existing work in the literature, we control two different classes of heuristics simultaneously by a single learning agent. We verify our approach numerically and show consistent node reductions over the MIPLIB 2017 Benchmark set. For harder instances that take at least 1000 seconds to solve, we observe a speedup of 4%.

The Machine Learning for Combinatorial Optimization Competition (ML4CO): Results and Insights

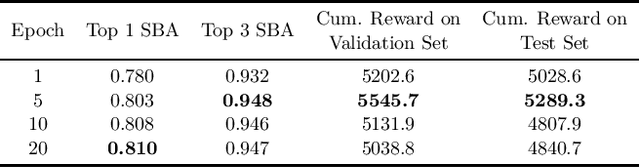
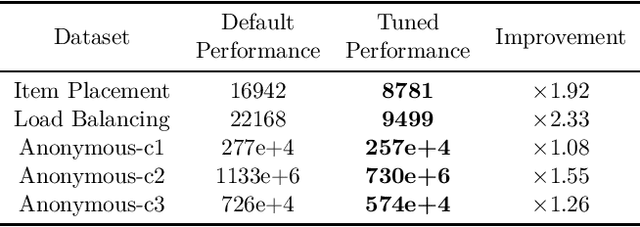
Combinatorial optimization is a well-established area in operations research and computer science. Until recently, its methods have focused on solving problem instances in isolation, ignoring that they often stem from related data distributions in practice. However, recent years have seen a surge of interest in using machine learning as a new approach for solving combinatorial problems, either directly as solvers or by enhancing exact solvers. Based on this context, the ML4CO aims at improving state-of-the-art combinatorial optimization solvers by replacing key heuristic components. The competition featured three challenging tasks: finding the best feasible solution, producing the tightest optimality certificate, and giving an appropriate solver configuration. Three realistic datasets were considered: balanced item placement, workload apportionment, and maritime inventory routing. This last dataset was kept anonymous for the contestants.

Learning to Schedule Heuristics in Branch-and-Bound

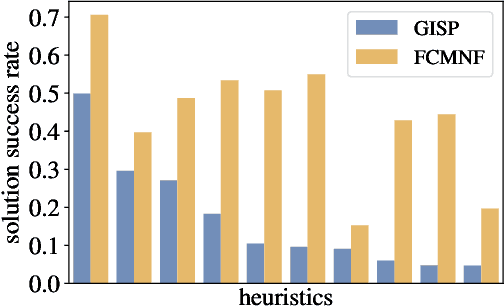
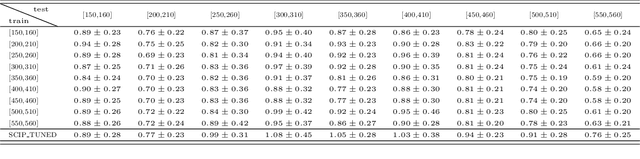
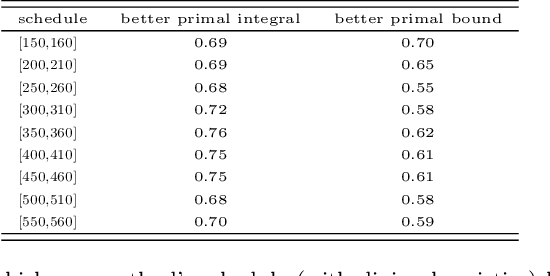
Primal heuristics play a crucial role in exact solvers for Mixed Integer Programming (MIP). While solvers are guaranteed to find optimal solutions given sufficient time, real-world applications typically require finding good solutions early on in the search to enable fast decision-making. While much of MIP research focuses on designing effective heuristics, the question of how to manage multiple MIP heuristics in a solver has not received equal attention. Generally, solvers follow hard-coded rules derived from empirical testing on broad sets of instances. Since the performance of heuristics is instance-dependent, using these general rules for a particular problem might not yield the best performance. In this work, we propose the first data-driven framework for scheduling heuristics in an exact MIP solver. By learning from data describing the performance of primal heuristics, we obtain a problem-specific schedule of heuristics that collectively find many solutions at minimal cost. We provide a formal description of the problem and propose an efficient algorithm for computing such a schedule. Compared to the default settings of a state-of-the-art academic MIP solver, we are able to reduce the average primal integral by up to 49% on a class of challenging instances.