Pawel Lichocki
Online Learning for Scheduling MIP Heuristics
Apr 04, 2023Abstract:Mixed Integer Programming (MIP) is NP-hard, and yet modern solvers often solve large real-world problems within minutes. This success can partially be attributed to heuristics. Since their behavior is highly instance-dependent, relying on hard-coded rules derived from empirical testing on a large heterogeneous corpora of benchmark instances might lead to sub-optimal performance. In this work, we propose an online learning approach that adapts the application of heuristics towards the single instance at hand. We replace the commonly used static heuristic handling with an adaptive framework exploiting past observations about the heuristic's behavior to make future decisions. In particular, we model the problem of controlling Large Neighborhood Search and Diving - two broad and complex classes of heuristics - as a multi-armed bandit problem. Going beyond existing work in the literature, we control two different classes of heuristics simultaneously by a single learning agent. We verify our approach numerically and show consistent node reductions over the MIPLIB 2017 Benchmark set. For harder instances that take at least 1000 seconds to solve, we observe a speedup of 4%.
The Machine Learning for Combinatorial Optimization Competition (ML4CO): Results and Insights
Mar 17, 2022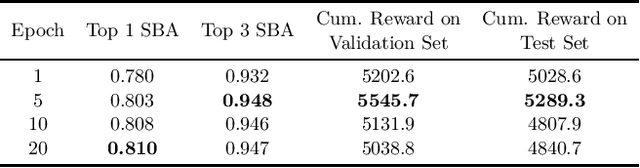

Abstract:Combinatorial optimization is a well-established area in operations research and computer science. Until recently, its methods have focused on solving problem instances in isolation, ignoring that they often stem from related data distributions in practice. However, recent years have seen a surge of interest in using machine learning as a new approach for solving combinatorial problems, either directly as solvers or by enhancing exact solvers. Based on this context, the ML4CO aims at improving state-of-the-art combinatorial optimization solvers by replacing key heuristic components. The competition featured three challenging tasks: finding the best feasible solution, producing the tightest optimality certificate, and giving an appropriate solver configuration. Three realistic datasets were considered: balanced item placement, workload apportionment, and maritime inventory routing. This last dataset was kept anonymous for the contestants.
Solving Mixed Integer Programs Using Neural Networks
Dec 23, 2020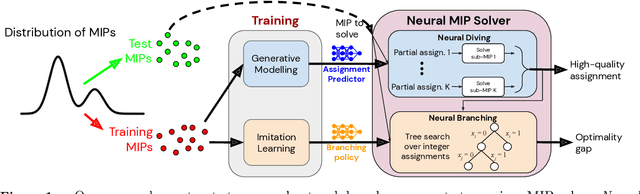
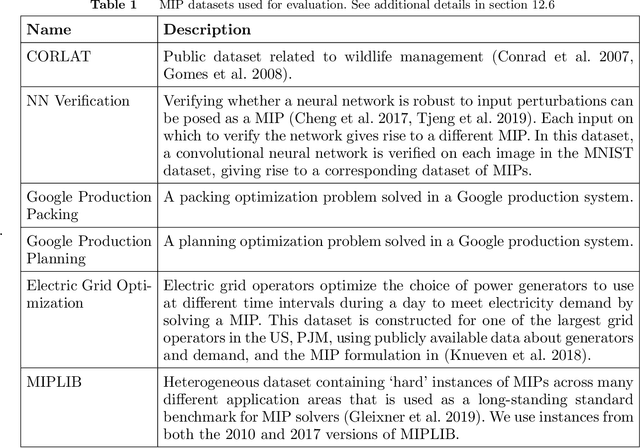
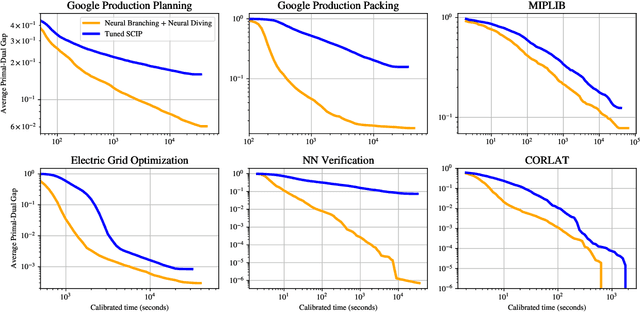
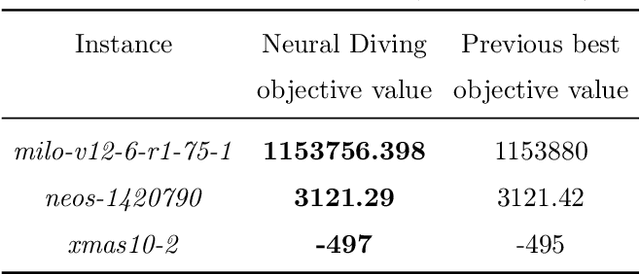
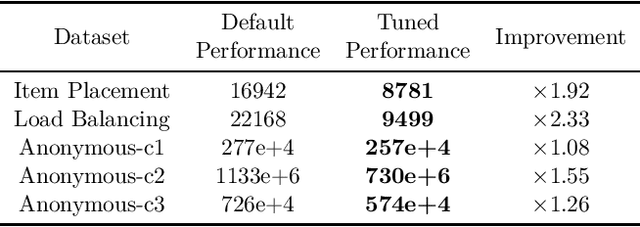
Abstract:Mixed Integer Programming (MIP) solvers rely on an array of sophisticated heuristics developed with decades of research to solve large-scale MIP instances encountered in practice. Machine learning offers to automatically construct better heuristics from data by exploiting shared structure among instances in the data. This paper applies learning to the two key sub-tasks of a MIP solver, generating a high-quality joint variable assignment, and bounding the gap in objective value between that assignment and an optimal one. Our approach constructs two corresponding neural network-based components, Neural Diving and Neural Branching, to use in a base MIP solver such as SCIP. Neural Diving learns a deep neural network to generate multiple partial assignments for its integer variables, and the resulting smaller MIPs for un-assigned variables are solved with SCIP to construct high quality joint assignments. Neural Branching learns a deep neural network to make variable selection decisions in branch-and-bound to bound the objective value gap with a small tree. This is done by imitating a new variant of Full Strong Branching we propose that scales to large instances using GPUs. We evaluate our approach on six diverse real-world datasets, including two Google production datasets and MIPLIB, by training separate neural networks on each. Most instances in all the datasets combined have $10^3-10^6$ variables and constraints after presolve, which is significantly larger than previous learning approaches. Comparing solvers with respect to primal-dual gap averaged over a held-out set of instances, the learning-augmented SCIP is 2x to 10x better on all datasets except one on which it is $10^5$x better, at large time limits. To the best of our knowledge, ours is the first learning approach to demonstrate such large improvements over SCIP on both large-scale real-world application datasets and MIPLIB.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge