Solving MaxSAT with Matrix Multiplication

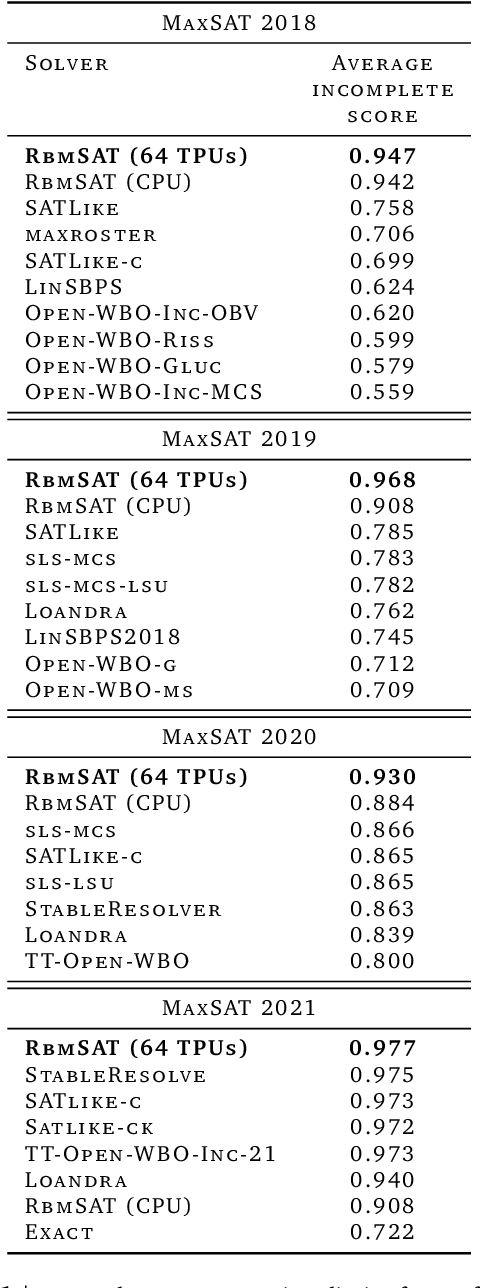
We propose an incomplete algorithm for Maximum Satisfiability (MaxSAT) specifically designed to run on neural network accelerators such as GPUs and TPUs. Given a MaxSAT problem instance in conjunctive normal form, our procedure constructs a Restricted Boltzmann Machine (RBM) with an equilibrium distribution wherein the probability of a Boolean assignment is exponential in the number of clauses it satisfies. Block Gibbs sampling is used to stochastically search the space of assignments with parallel Markov chains. Since matrix multiplication is the main computational primitive for block Gibbs sampling in an RBM, our approach leads to an elegantly simple algorithm (40 lines of JAX) well-suited for neural network accelerators. Theoretical results about RBMs guarantee that the required number of visible and hidden units of the RBM scale only linearly with the number of variables and constant-sized clauses in the MaxSAT instance, ensuring that the computational cost of a Gibbs step scales reasonably with the instance size. Search throughput can be increased by batching parallel chains within a single accelerator as well as by distributing them across multiple accelerators. As a further enhancement, a heuristic based on unit propagation running on CPU is periodically applied to the sampled assignments. Our approach, which we term RbmSAT, is a new design point in the algorithm-hardware co-design space for MaxSAT. We present timed results on a subset of problem instances from the annual MaxSAT Evaluation's Incomplete Unweighted Track for the years 2018 to 2021. When allotted the same running time and CPU compute budget (but no TPUs), RbmSAT outperforms other participating solvers on problems drawn from three out of the four years' competitions. Given the same running time on a TPU cluster for which RbmSAT is uniquely designed, it outperforms all solvers on problems drawn from all four years.

Automap: Towards Ergonomic Automated Parallelism for ML Models

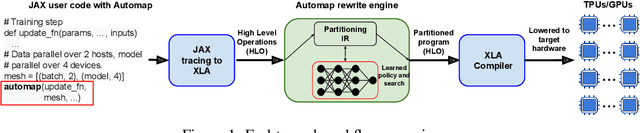
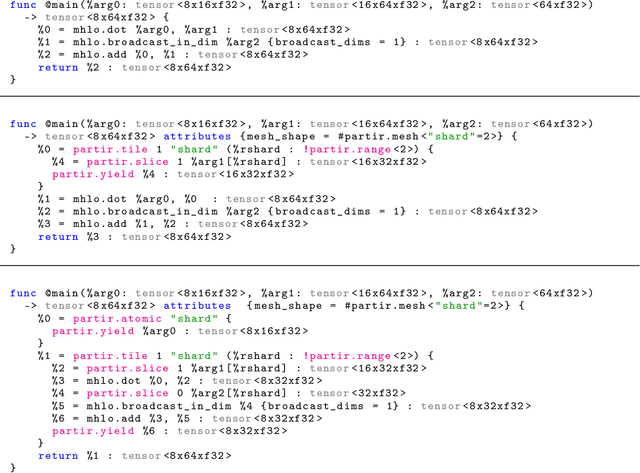
The rapid rise in demand for training large neural network architectures has brought into focus the need for partitioning strategies, for example by using data, model, or pipeline parallelism. Implementing these methods is increasingly supported through program primitives, but identifying efficient partitioning strategies requires expensive experimentation and expertise. We present the prototype of an automated partitioner that seamlessly integrates into existing compilers and existing user workflows. Our partitioner enables SPMD-style parallelism that encompasses data parallelism and parameter/activation sharding. Through a combination of inductive tactics and search in a platform-independent partitioning IR, automap can recover expert partitioning strategies such as Megatron sharding for transformer layers.

Learning a Large Neighborhood Search Algorithm for Mixed Integer Programs

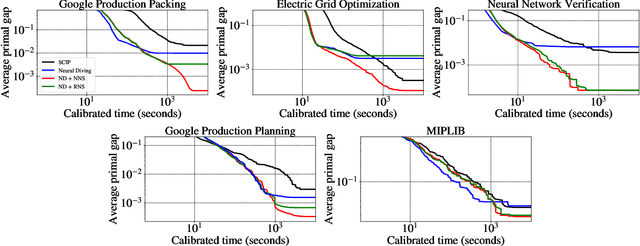
Large Neighborhood Search (LNS) is a combinatorial optimization heuristic that starts with an assignment of values for the variables to be optimized, and iteratively improves it by searching a large neighborhood around the current assignment. In this paper we consider a learning-based LNS approach for mixed integer programs (MIPs). We train a Neural Diving model to represent a probability distribution over assignments, which, together with an off-the-shelf MIP solver, generates an initial assignment. Formulating the subsequent search steps as a Markov Decision Process, we train a Neural Neighborhood Selection policy to select a search neighborhood at each step, which is searched using a MIP solver to find the next assignment. The policy network is trained using imitation learning. We propose a target policy for imitation that, given enough compute resources, is guaranteed to select the neighborhood containing the optimal next assignment amongst all possible choices for the neighborhood of a specified size. Our approach matches or outperforms all the baselines on five real-world MIP datasets with large-scale instances from diverse applications, including two production applications at Google. It achieves $2\times$ to $37.8\times$ better average primal gap than the best baseline on three of the datasets at large running times.

Solving Mixed Integer Programs Using Neural Networks

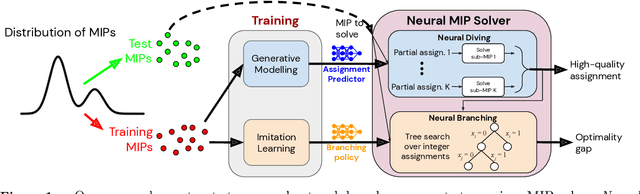
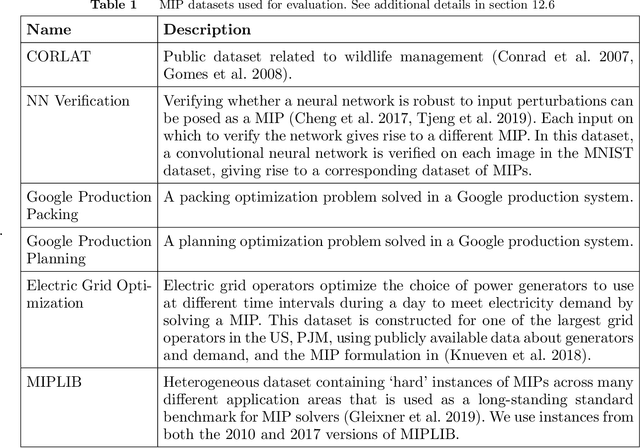
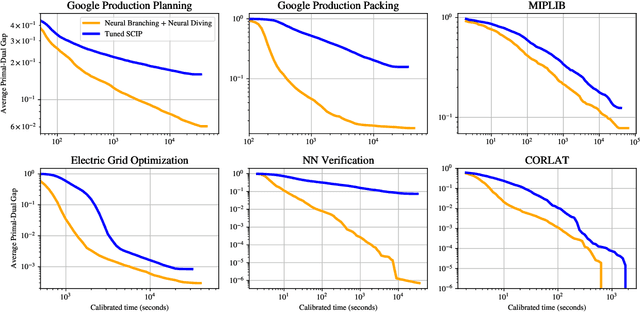
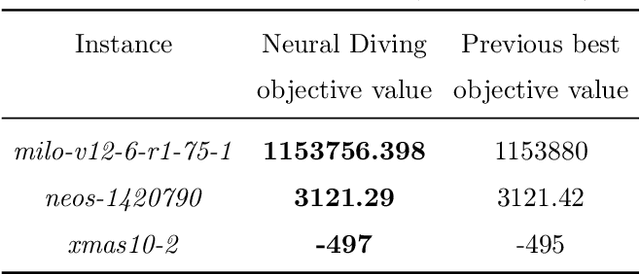
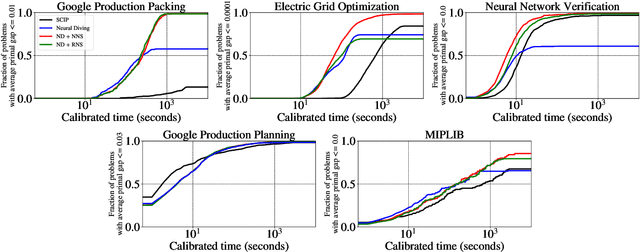
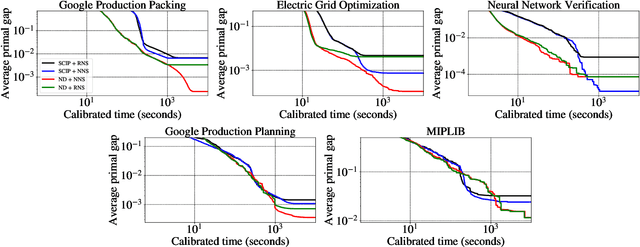
Mixed Integer Programming (MIP) solvers rely on an array of sophisticated heuristics developed with decades of research to solve large-scale MIP instances encountered in practice. Machine learning offers to automatically construct better heuristics from data by exploiting shared structure among instances in the data. This paper applies learning to the two key sub-tasks of a MIP solver, generating a high-quality joint variable assignment, and bounding the gap in objective value between that assignment and an optimal one. Our approach constructs two corresponding neural network-based components, Neural Diving and Neural Branching, to use in a base MIP solver such as SCIP. Neural Diving learns a deep neural network to generate multiple partial assignments for its integer variables, and the resulting smaller MIPs for un-assigned variables are solved with SCIP to construct high quality joint assignments. Neural Branching learns a deep neural network to make variable selection decisions in branch-and-bound to bound the objective value gap with a small tree. This is done by imitating a new variant of Full Strong Branching we propose that scales to large instances using GPUs. We evaluate our approach on six diverse real-world datasets, including two Google production datasets and MIPLIB, by training separate neural networks on each. Most instances in all the datasets combined have $10^3-10^6$ variables and constraints after presolve, which is significantly larger than previous learning approaches. Comparing solvers with respect to primal-dual gap averaged over a held-out set of instances, the learning-augmented SCIP is 2x to 10x better on all datasets except one on which it is $10^5$x better, at large time limits. To the best of our knowledge, ours is the first learning approach to demonstrate such large improvements over SCIP on both large-scale real-world application datasets and MIPLIB.

Prioritized Unit Propagation with Periodic Resetting is (Almost) All You Need for Random SAT Solving

We propose prioritized unit propagation with periodic resetting, which is a simple but surprisingly effective algorithm for solving random SAT instances that are meant to be hard. In particular, an evaluation on the Random Track of the 2017 and 2018 SAT competitions shows that a basic prototype of this simple idea already ranks at second place in both years. We share this observation in the hope that it helps the SAT community better understand the hardness of random instances used in competitions and inspire other interesting ideas on SAT solving.

REGAL: Transfer Learning For Fast Optimization of Computation Graphs

We present a deep reinforcement learning approach to optimizing the execution cost of computation graphs in a static compiler. The key idea is to combine a neural network policy with a genetic algorithm, the Biased Random-Key Genetic Algorithm (BRKGA). The policy is trained to predict, given an input graph to be optimized, the node-level probability distributions for sampling mutations and crossovers in BRKGA. Our approach, "REINFORCE-based Genetic Algorithm Learning" (REGAL), uses the policy's ability to transfer to new graphs to significantly improve the solution quality of the genetic algorithm for the same objective evaluation budget. As a concrete application, we show results for minimizing peak memory in TensorFlow graphs by jointly optimizing device placement and scheduling. REGAL achieves on average 3.56% lower peak memory than BRKGA on previously unseen graphs, outperforming all the algorithms we compare to, and giving 4.4x bigger improvement than the next best algorithm. We also evaluate REGAL on a production compiler team's performance benchmark of XLA graphs and achieve on average 3.74% lower peak memory than BRKGA, again outperforming all others. Our approach and analysis is made possible by collecting a dataset of 372 unique real-world TensorFlow graphs, more than an order of magnitude more data than previous work.

A Quantitative Evaluation Framework for Missing Value Imputation Algorithms

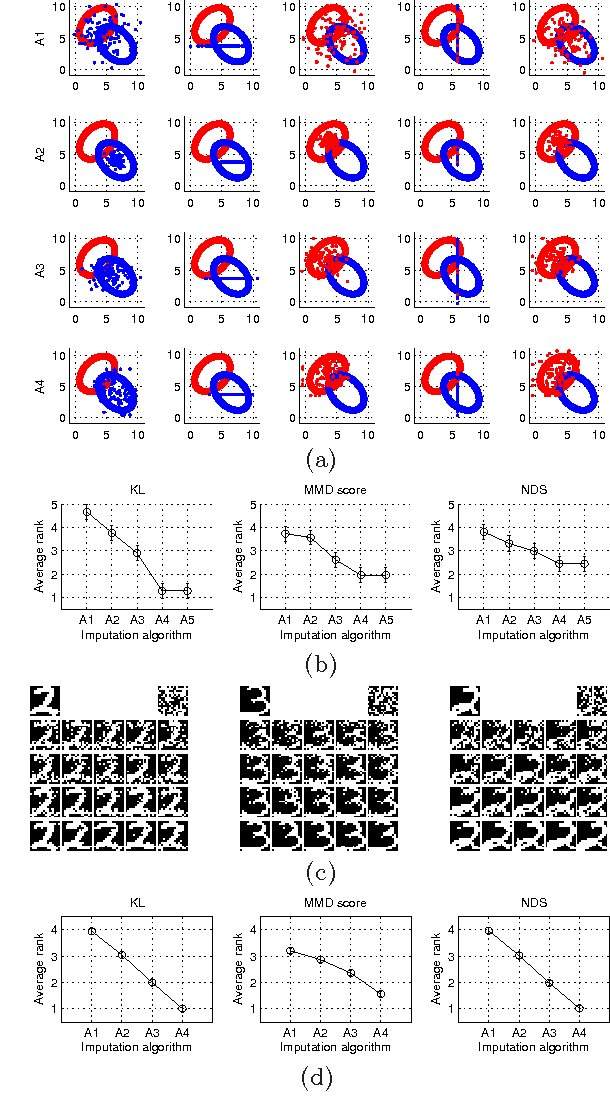
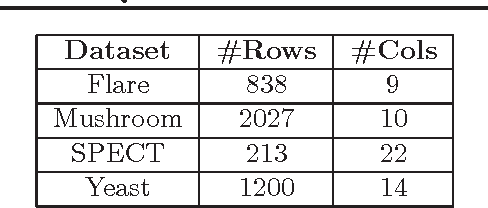
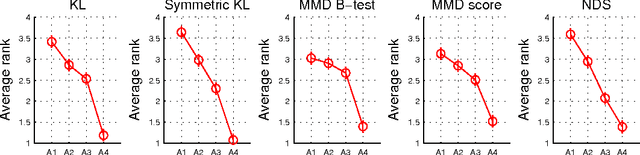
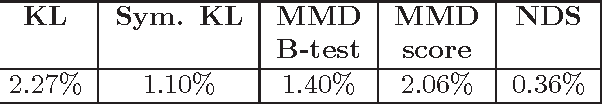
We consider the problem of quantitatively evaluating missing value imputation algorithms. Given a dataset with missing values and a choice of several imputation algorithms to fill them in, there is currently no principled way to rank the algorithms using a quantitative metric. We develop a framework based on treating imputation evaluation as a problem of comparing two distributions and show how it can be used to compute quantitative metrics. We present an efficient procedure for applying this framework to practical datasets, demonstrate several metrics derived from the existing literature on comparing distributions, and propose a new metric called Neighborhood-based Dissimilarity Score which is fast to compute and provides similar results. Results are shown on several datasets, metrics, and imputations algorithms.

A Structured Prediction Approach for Missing Value Imputation

Missing value imputation is an important practical problem. There is a large body of work on it, but there does not exist any work that formulates the problem in a structured output setting. Also, most applications have constraints on the imputed data, for example on the distribution associated with each variable. None of the existing imputation methods use these constraints. In this paper we propose a structured output approach for missing value imputation that also incorporates domain constraints. We focus on large margin models, but it is easy to extend the ideas to probabilistic models. We deal with the intractable inference step in learning via a piecewise training technique that is simple, efficient, and effective. Comparison with existing state-of-the-art and baseline imputation methods shows that our method gives significantly improved performance on the Hamming loss measure.