REGAL: Transfer Learning For Fast Optimization of Computation Graphs

We present a deep reinforcement learning approach to optimizing the execution cost of computation graphs in a static compiler. The key idea is to combine a neural network policy with a genetic algorithm, the Biased Random-Key Genetic Algorithm (BRKGA). The policy is trained to predict, given an input graph to be optimized, the node-level probability distributions for sampling mutations and crossovers in BRKGA. Our approach, "REINFORCE-based Genetic Algorithm Learning" (REGAL), uses the policy's ability to transfer to new graphs to significantly improve the solution quality of the genetic algorithm for the same objective evaluation budget. As a concrete application, we show results for minimizing peak memory in TensorFlow graphs by jointly optimizing device placement and scheduling. REGAL achieves on average 3.56% lower peak memory than BRKGA on previously unseen graphs, outperforming all the algorithms we compare to, and giving 4.4x bigger improvement than the next best algorithm. We also evaluate REGAL on a production compiler team's performance benchmark of XLA graphs and achieve on average 3.74% lower peak memory than BRKGA, again outperforming all others. Our approach and analysis is made possible by collecting a dataset of 372 unique real-world TensorFlow graphs, more than an order of magnitude more data than previous work.

Graph Representations for Higher-Order Logic and Theorem Proving

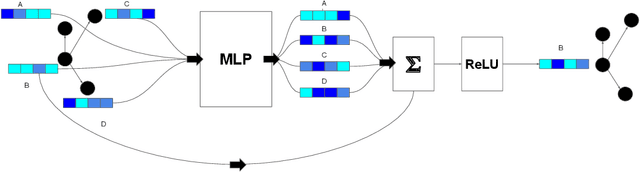
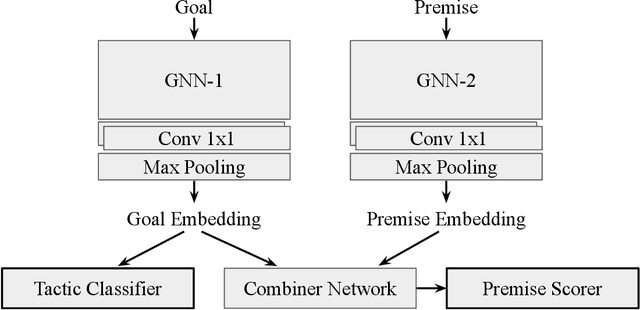
This paper presents the first use of graph neural networks (GNNs) for higher-order proof search and demonstrates that GNNs can improve upon state-of-the-art results in this domain. Interactive, higher-order theorem provers allow for the formalization of most mathematical theories and have been shown to pose a significant challenge for deep learning. Higher-order logic is highly expressive and, even though it is well-structured with a clearly defined grammar and semantics, there still remains no well-established method to convert formulas into graph-based representations. In this paper, we consider several graphical representations of higher-order logic and evaluate them against the HOList benchmark for higher-order theorem proving.