Language Modeling for Formal Mathematics

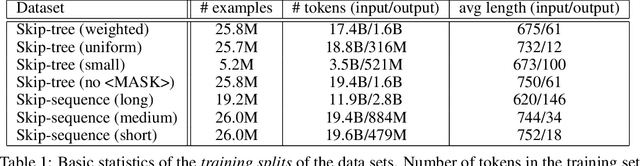
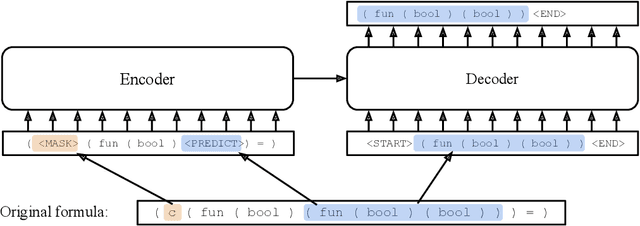
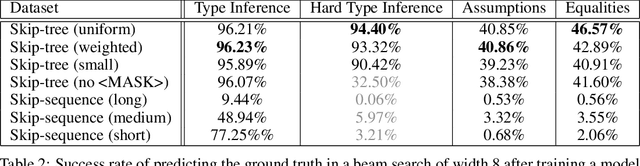
We examine whether language modeling applied to mathematical formulas enables logical reasoning. We suggest several logical reasoning tasks that can be used to evaluate language models trained on formal mathematical statements, such as type inference, suggesting missing assumptions and completing equalities. To train language models for formal mathematics, we propose a novel skip-tree task, which outperforms standard language modeling tasks on our reasoning benchmarks. We also analyze the models' ability to formulate new conjectures by measuring how often the predictions that do not fit the ground truth or any training data turn out to be true and useful statements.

Mathematical Reasoning in Latent Space

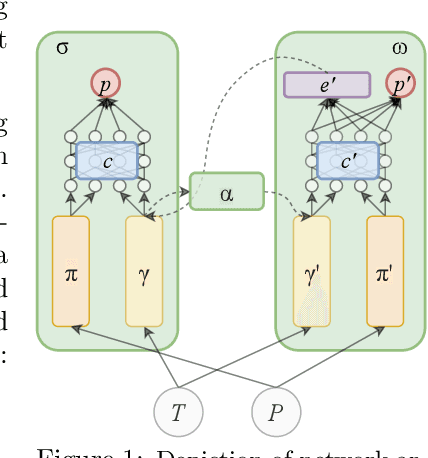
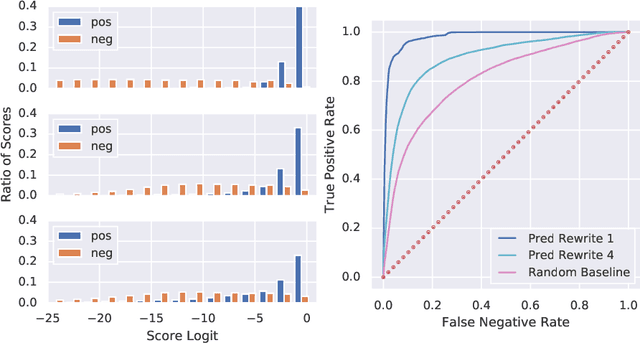
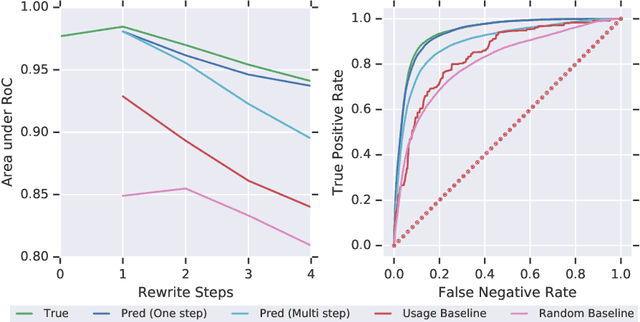
We design and conduct a simple experiment to study whether neural networks can perform several steps of approximate reasoning in a fixed dimensional latent space. The set of rewrites (i.e. transformations) that can be successfully performed on a statement represents essential semantic features of the statement. We can compress this information by embedding the formula in a vector space, such that the vector associated with a statement can be used to predict whether a statement can be rewritten by other theorems. Predicting the embedding of a formula generated by some rewrite rule is naturally viewed as approximate reasoning in the latent space. In order to measure the effectiveness of this reasoning, we perform approximate deduction sequences in the latent space and use the resulting embedding to inform the semantic features of the corresponding formal statement (which is obtained by performing the corresponding rewrite sequence using real formulas). Our experiments show that graph neural networks can make non-trivial predictions about the rewrite-success of statements, even when they propagate predicted latent representations for several steps. Since our corpus of mathematical formulas includes a wide variety of mathematical disciplines, this experiment is a strong indicator for the feasibility of deduction in latent space in general.

Learning to Reason in Large Theories without Imitation

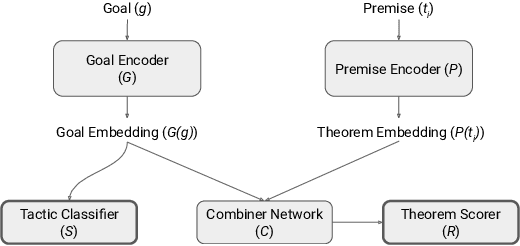
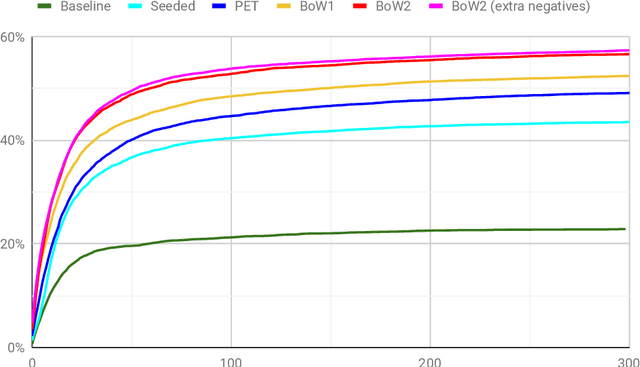
Automated theorem proving in large theories can be learned via reinforcement learning over an indefinitely growing action space. In order to select actions, one performs nearest neighbor lookups in the knowledge base to find premises to be applied. Here we address the exploration for reinforcement learning in this space. Approaches (like epsilon-greedy strategy) that sample actions uniformly do not scale to this scenario as most actions lead to dead ends and unsuccessful proofs which are not useful for training our models. In this paper, we compare approaches that select premises using randomly initialized similarity measures and mixing them with the proposals of the learned model. We evaluate these on the HOList benchmark for tactics based higher order theorem proving. We implement an automated theorem prover named DeepHOL-Zero that does not use any of the human proofs and show that our improved exploration method manages to expand the training set continuously. DeepHOL-Zero outperforms the best theorem prover trained by imitation learning alone.

Graph Representations for Higher-Order Logic and Theorem Proving

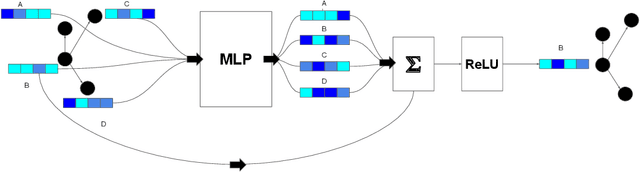
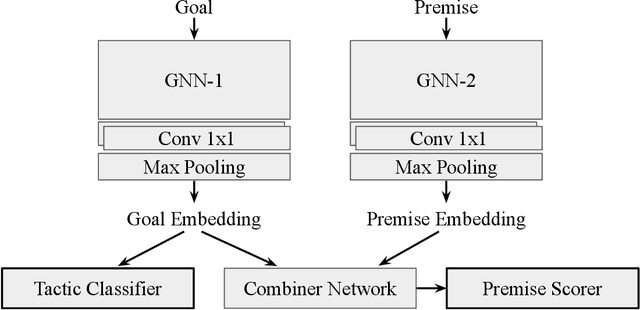
This paper presents the first use of graph neural networks (GNNs) for higher-order proof search and demonstrates that GNNs can improve upon state-of-the-art results in this domain. Interactive, higher-order theorem provers allow for the formalization of most mathematical theories and have been shown to pose a significant challenge for deep learning. Higher-order logic is highly expressive and, even though it is well-structured with a clearly defined grammar and semantics, there still remains no well-established method to convert formulas into graph-based representations. In this paper, we consider several graphical representations of higher-order logic and evaluate them against the HOList benchmark for higher-order theorem proving.

HOList: An Environment for Machine Learning of Higher-Order Theorem Proving

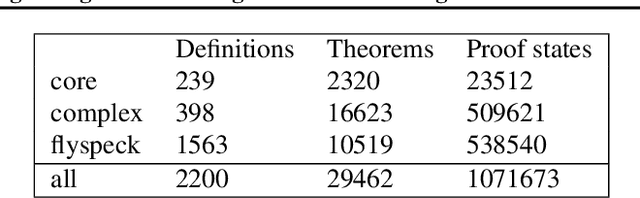
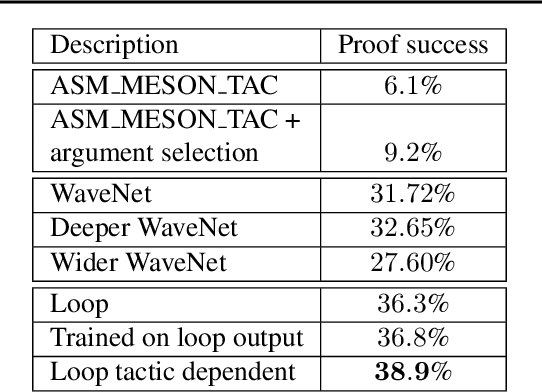
We present an environment, benchmark, and deep learning driven automated theorem prover for higher-order logic. Higher-order interactive theorem provers enable the formalization of arbitrary mathematical theories and thereby present an interesting, open-ended challenge for deep learning. We provide an open-source framework based on the HOL Light theorem prover that can be used as a reinforcement learning environment. HOL Light comes with a broad coverage of basic mathematical theorems on calculus and the formal proof of the Kepler conjecture, from which we derive a challenging benchmark for automated reasoning. We also present a deep reinforcement learning driven automated theorem prover, DeepHOL, with strong initial results on this benchmark.