Language Modeling for Formal Mathematics
Paper and Code
Jun 10, 2020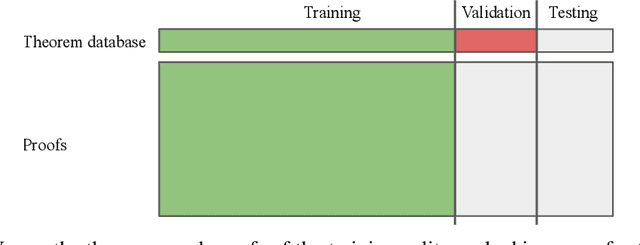
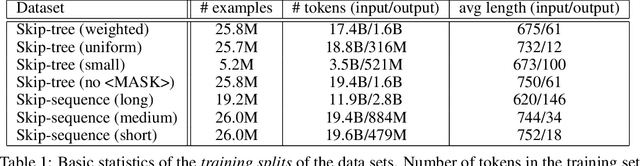
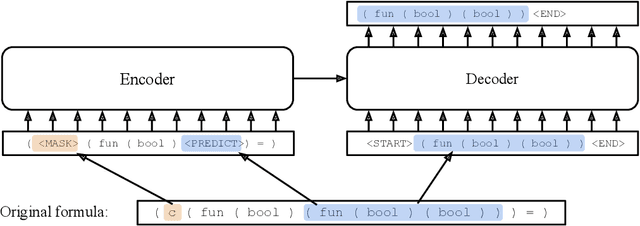
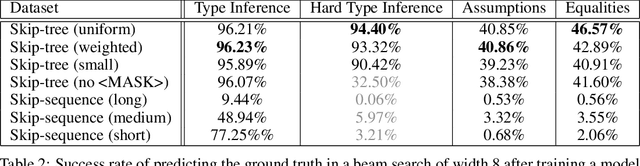
We examine whether language modeling applied to mathematical formulas enables logical reasoning. We suggest several logical reasoning tasks that can be used to evaluate language models trained on formal mathematical statements, such as type inference, suggesting missing assumptions and completing equalities. To train language models for formal mathematics, we propose a novel skip-tree task, which outperforms standard language modeling tasks on our reasoning benchmarks. We also analyze the models' ability to formulate new conjectures by measuring how often the predictions that do not fit the ground truth or any training data turn out to be true and useful statements.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge