Christian Szegedy
Towards Guaranteed Safe AI: A Framework for Ensuring Robust and Reliable AI Systems
May 10, 2024



Abstract:Ensuring that AI systems reliably and robustly avoid harmful or dangerous behaviours is a crucial challenge, especially for AI systems with a high degree of autonomy and general intelligence, or systems used in safety-critical contexts. In this paper, we will introduce and define a family of approaches to AI safety, which we will refer to as guaranteed safe (GS) AI. The core feature of these approaches is that they aim to produce AI systems which are equipped with high-assurance quantitative safety guarantees. This is achieved by the interplay of three core components: a world model (which provides a mathematical description of how the AI system affects the outside world), a safety specification (which is a mathematical description of what effects are acceptable), and a verifier (which provides an auditable proof certificate that the AI satisfies the safety specification relative to the world model). We outline a number of approaches for creating each of these three core components, describe the main technical challenges, and suggest a number of potential solutions to them. We also argue for the necessity of this approach to AI safety, and for the inadequacy of the main alternative approaches.
Don't Trust: Verify -- Grounding LLM Quantitative Reasoning with Autoformalization
Mar 26, 2024Abstract:Large language models (LLM), such as Google's Minerva and OpenAI's GPT families, are becoming increasingly capable of solving mathematical quantitative reasoning problems. However, they still make unjustified logical and computational errors in their reasoning steps and answers. In this paper, we leverage the fact that if the training corpus of LLMs contained sufficiently many examples of formal mathematics (e.g. in Isabelle, a formal theorem proving environment), they can be prompted to translate i.e. autoformalize informal mathematical statements into formal Isabelle code -- which can be verified automatically for internal consistency. This provides a mechanism to automatically reject solutions whose formalized versions are inconsistent within themselves or with the formalized problem statement. We evaluate our method on GSM8K, MATH and MultiArith datasets and demonstrate that our approach provides a consistently better heuristic than vanilla majority voting -- the previously best method to identify correct answers, by more than 12% on GSM8K. In our experiments it improves results consistently across all datasets and LLM model sizes. The code can be found at https://github.com/jinpz/dtv.
Magnushammer: A Transformer-based Approach to Premise Selection
Mar 08, 2023Abstract:Premise selection is a fundamental problem of automated theorem proving. Previous works often use intricate symbolic methods, rely on domain knowledge, and require significant engineering effort to solve this task. In this work, we show that Magnushammer, a neural transformer-based approach, can outperform traditional symbolic systems by a large margin. Tested on the PISA benchmark, Magnushammer achieves $59.5\%$ proof rate compared to a $38.3\%$ proof rate of Sledgehammer, the most mature and popular symbolic-based solver. Furthermore, by combining Magnushammer with a neural formal prover based on a language model, we significantly improve the previous state-of-the-art proof rate from $57.0\%$ to $71.0\%$.
Autoformalization with Large Language Models
May 25, 2022
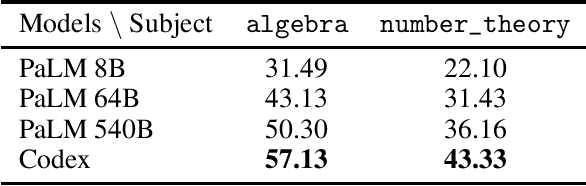


Abstract:Autoformalization is the process of automatically translating from natural language mathematics to formal specifications and proofs. A successful autoformalization system could advance the fields of formal verification, program synthesis, and artificial intelligence. While the long-term goal of autoformalization seemed elusive for a long time, we show large language models provide new prospects towards this goal. We make the surprising observation that LLMs can correctly translate a significant portion ($25.3\%$) of mathematical competition problems perfectly to formal specifications in Isabelle/HOL. We demonstrate the usefulness of this process by improving a previously introduced neural theorem prover via training on these autoformalized theorems. Our methodology results in a new state-of-the-art result on the MiniF2F theorem proving benchmark, improving the proof rate from $29.6\%$ to $35.2\%$.
Memorizing Transformers
Mar 16, 2022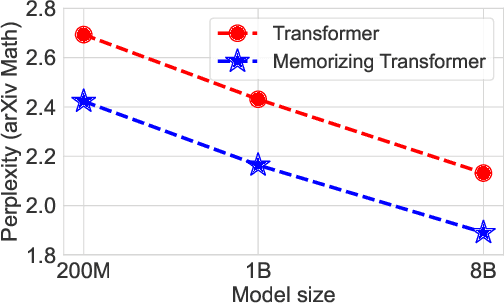
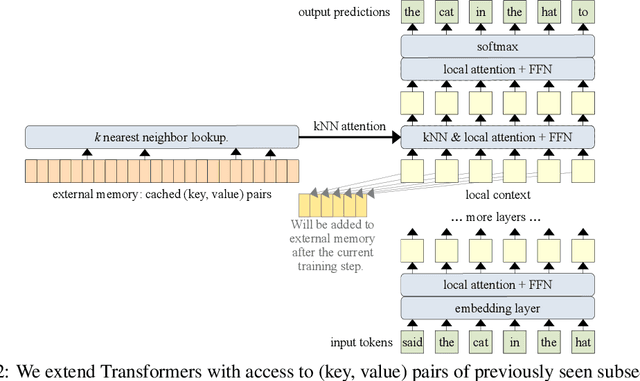

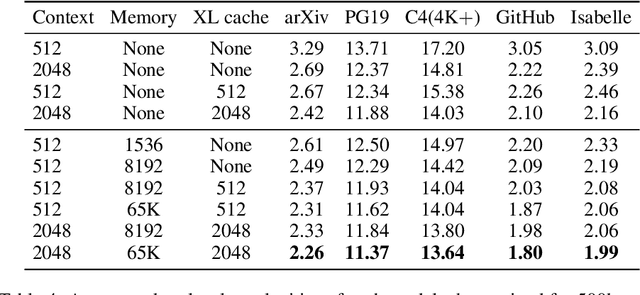
Abstract:Language models typically need to be trained or finetuned in order to acquire new knowledge, which involves updating their weights. We instead envision language models that can simply read and memorize new data at inference time, thus acquiring new knowledge immediately. In this work, we extend language models with the ability to memorize the internal representations of past inputs. We demonstrate that an approximate kNN lookup into a non-differentiable memory of recent (key, value) pairs improves language modeling across various benchmarks and tasks, including generic webtext (C4), math papers (arXiv), books (PG-19), code (Github), as well as formal theorems (Isabelle). We show that the performance steadily improves when we increase the size of memory up to 262K tokens. On benchmarks including code and mathematics, we find that the model is capable of making use of newly defined functions and theorems during test time.
Hierarchical Transformers Are More Efficient Language Models
Oct 26, 2021

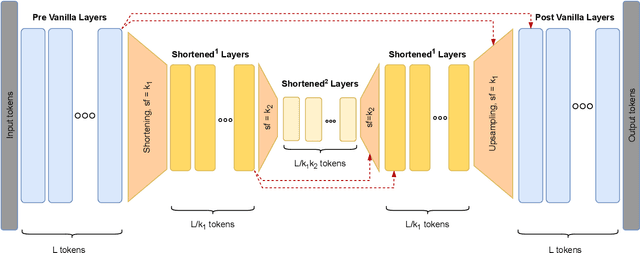

Abstract:Transformer models yield impressive results on many NLP and sequence modeling tasks. Remarkably, Transformers can handle long sequences which allows them to produce long coherent outputs: full paragraphs produced by GPT-3 or well-structured images produced by DALL-E. These large language models are impressive but also very inefficient and costly, which limits their applications and accessibility. We postulate that having an explicit hierarchical architecture is the key to Transformers that efficiently handle long sequences. To verify this claim, we first study different ways to downsample and upsample activations in Transformers so as to make them hierarchical. We use the best performing upsampling and downsampling layers to create Hourglass - a hierarchical Transformer language model. Hourglass improves upon the Transformer baseline given the same amount of computation and can yield the same results as Transformers more efficiently. In particular, Hourglass sets new state-of-the-art for Transformer models on the ImageNet32 generation task and improves language modeling efficiency on the widely studied enwik8 benchmark.
LIME: Learning Inductive Bias for Primitives of Mathematical Reasoning
Jan 15, 2021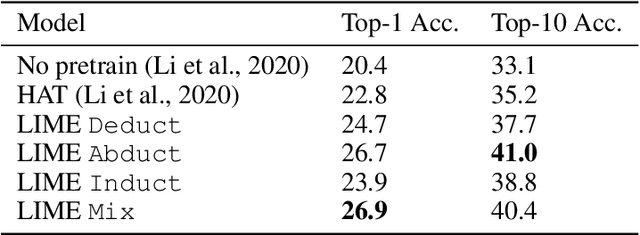



Abstract:While designing inductive bias in neural architectures has been widely studied, we hypothesize that transformer networks are flexible enough to learn inductive bias from suitable generic tasks. Here, we replace architecture engineering by encoding inductive bias in the form of datasets. Inspired by Peirce's view that deduction, induction, and abduction form an irreducible set of reasoning primitives, we design three synthetic tasks that are intended to require the model to have these three abilities. We specifically design these synthetic tasks in a way that they are devoid of mathematical knowledge to ensure that only the fundamental reasoning biases can be learned from these tasks. This defines a new pre-training methodology called "LIME" (Learning Inductive bias for Mathematical rEasoning). Models trained with LIME significantly outperform vanilla transformers on three very different large mathematical reasoning benchmarks. Unlike dominating the computation cost as traditional pre-training approaches, LIME requires only a small fraction of the computation cost of the typical downstream task.
Language Modeling for Formal Mathematics
Jun 10, 2020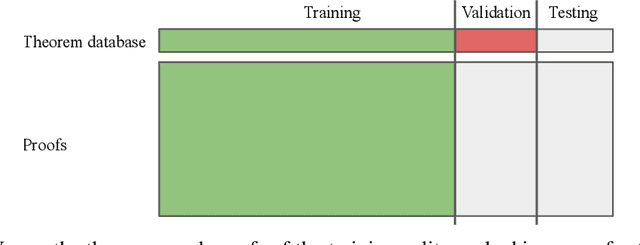
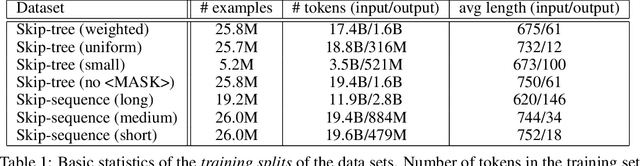
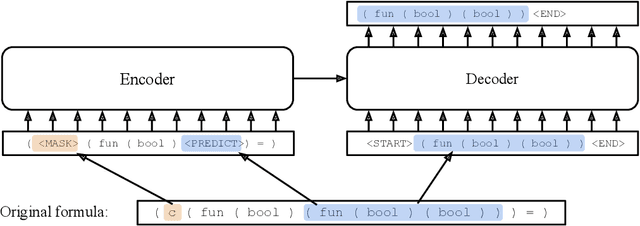
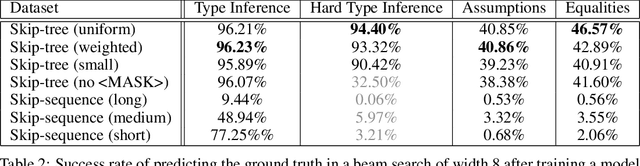
Abstract:We examine whether language modeling applied to mathematical formulas enables logical reasoning. We suggest several logical reasoning tasks that can be used to evaluate language models trained on formal mathematical statements, such as type inference, suggesting missing assumptions and completing equalities. To train language models for formal mathematics, we propose a novel skip-tree task, which outperforms standard language modeling tasks on our reasoning benchmarks. We also analyze the models' ability to formulate new conjectures by measuring how often the predictions that do not fit the ground truth or any training data turn out to be true and useful statements.
Mathematical Reasoning in Latent Space
Sep 26, 2019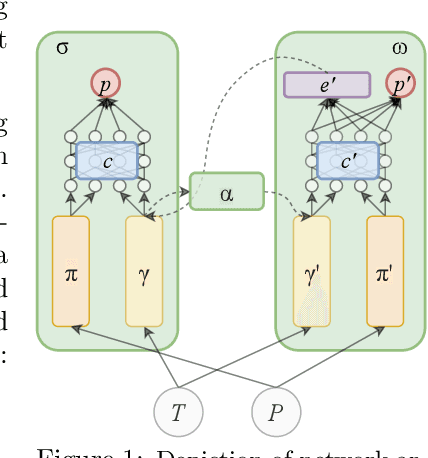
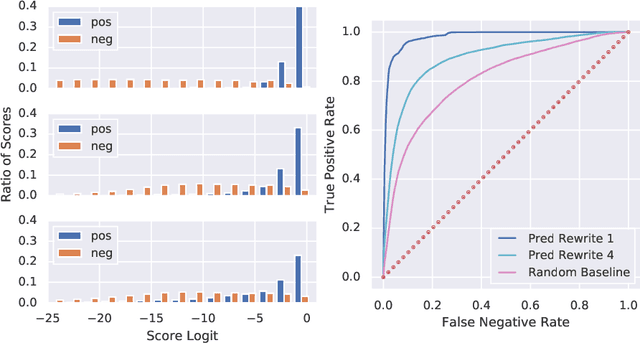
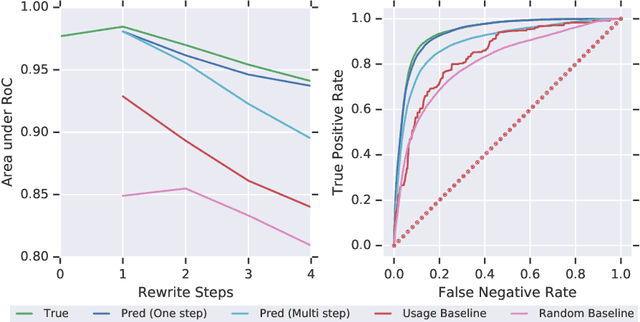
Abstract:We design and conduct a simple experiment to study whether neural networks can perform several steps of approximate reasoning in a fixed dimensional latent space. The set of rewrites (i.e. transformations) that can be successfully performed on a statement represents essential semantic features of the statement. We can compress this information by embedding the formula in a vector space, such that the vector associated with a statement can be used to predict whether a statement can be rewritten by other theorems. Predicting the embedding of a formula generated by some rewrite rule is naturally viewed as approximate reasoning in the latent space. In order to measure the effectiveness of this reasoning, we perform approximate deduction sequences in the latent space and use the resulting embedding to inform the semantic features of the corresponding formal statement (which is obtained by performing the corresponding rewrite sequence using real formulas). Our experiments show that graph neural networks can make non-trivial predictions about the rewrite-success of statements, even when they propagate predicted latent representations for several steps. Since our corpus of mathematical formulas includes a wide variety of mathematical disciplines, this experiment is a strong indicator for the feasibility of deduction in latent space in general.
Learning to Reason in Large Theories without Imitation
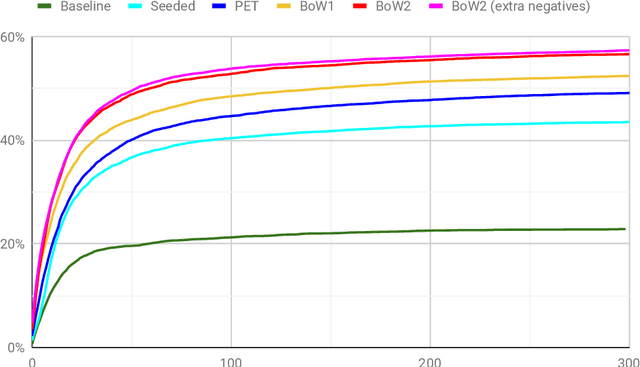
May 25, 2019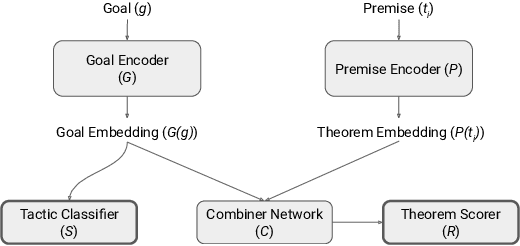


Abstract:Automated theorem proving in large theories can be learned via reinforcement learning over an indefinitely growing action space. In order to select actions, one performs nearest neighbor lookups in the knowledge base to find premises to be applied. Here we address the exploration for reinforcement learning in this space. Approaches (like epsilon-greedy strategy) that sample actions uniformly do not scale to this scenario as most actions lead to dead ends and unsuccessful proofs which are not useful for training our models. In this paper, we compare approaches that select premises using randomly initialized similarity measures and mixing them with the proposals of the learned model. We evaluate these on the HOList benchmark for tactics based higher order theorem proving. We implement an automated theorem prover named DeepHOL-Zero that does not use any of the human proofs and show that our improved exploration method manages to expand the training set continuously. DeepHOL-Zero outperforms the best theorem prover trained by imitation learning alone.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge