Don't Trust: Verify -- Grounding LLM Quantitative Reasoning with Autoformalization

Large language models (LLM), such as Google's Minerva and OpenAI's GPT families, are becoming increasingly capable of solving mathematical quantitative reasoning problems. However, they still make unjustified logical and computational errors in their reasoning steps and answers. In this paper, we leverage the fact that if the training corpus of LLMs contained sufficiently many examples of formal mathematics (e.g. in Isabelle, a formal theorem proving environment), they can be prompted to translate i.e. autoformalize informal mathematical statements into formal Isabelle code -- which can be verified automatically for internal consistency. This provides a mechanism to automatically reject solutions whose formalized versions are inconsistent within themselves or with the formalized problem statement. We evaluate our method on GSM8K, MATH and MultiArith datasets and demonstrate that our approach provides a consistently better heuristic than vanilla majority voting -- the previously best method to identify correct answers, by more than 12% on GSM8K. In our experiments it improves results consistently across all datasets and LLM model sizes. The code can be found at https://github.com/jinpz/dtv.

Autoformalization with Large Language Models

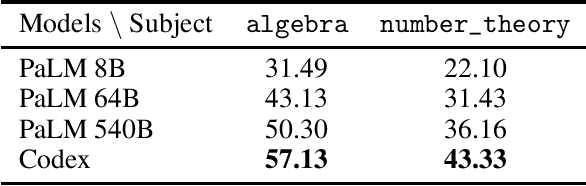
Autoformalization is the process of automatically translating from natural language mathematics to formal specifications and proofs. A successful autoformalization system could advance the fields of formal verification, program synthesis, and artificial intelligence. While the long-term goal of autoformalization seemed elusive for a long time, we show large language models provide new prospects towards this goal. We make the surprising observation that LLMs can correctly translate a significant portion ($25.3\%$) of mathematical competition problems perfectly to formal specifications in Isabelle/HOL. We demonstrate the usefulness of this process by improving a previously introduced neural theorem prover via training on these autoformalized theorems. Our methodology results in a new state-of-the-art result on the MiniF2F theorem proving benchmark, improving the proof rate from $29.6\%$ to $35.2\%$.

When adversarial examples are excusable

Neural networks work remarkably well in practice and theoretically they can be universal approximators. However, they still make mistakes and a specific type of them called adversarial errors seem inexcusable to humans. In this work, we analyze both test errors and adversarial errors on a well controlled but highly non-linear visual classification problem. We find that, when approximating training on infinite data, test errors tend to be close to the ground truth decision boundary. Qualitatively speaking these are also more difficult for a human. By contrast, adversarial examples can be found almost everywhere and are often obvious mistakes. However, when we constrain adversarial examples to the manifold, we observe a 90\% reduction in adversarial errors. If we inflate the manifold by training with Gaussian noise we observe a similar effect. In both cases, the remaining adversarial errors tend to be close to the ground truth decision boundary. Qualitatively, the remaining adversarial errors are similar to test errors on difficult examples. They do not have the customary quality of being inexcusable mistakes.

Self-attention Does Not Need $O$ Memory

We present a very simple algorithm for attention that requires $O(1)$ memory with respect to sequence length and an extension to self-attention that requires $O(\log n)$ memory. This is in contrast with the frequently stated belief that self-attention requires $O(n^2)$ memory. While the time complexity is still $O(n^2)$, device memory rather than compute capability is often the limiting factor on modern accelerators. Thus, reducing the memory requirements of attention allows processing of longer sequences than might otherwise be feasible. We provide a practical implementation for accelerators that requires $O(\sqrt{n})$ memory, is numerically stable, and is within a few percent of the runtime of the standard implementation of attention. We also demonstrate how to differentiate the function while remaining memory-efficient. For sequence length 16384, the memory overhead of self-attention is reduced by 59X for inference and by 32X for differentiation.