Neural Theorem Proving for Verification Conditions: A Real-World Benchmark

Theorem proving is fundamental to program verification, where the automated proof of Verification Conditions (VCs) remains a primary bottleneck. Real-world program verification frequently encounters hard VCs that existing Automated Theorem Provers (ATPs) cannot prove, leading to a critical need for extensive manual proofs that burden practical application. While Neural Theorem Proving (NTP) has achieved significant success in mathematical competitions, demonstrating the potential of machine learning approaches to formal reasoning, its application to program verification--particularly VC proving--remains largely unexplored. Despite existing work on annotation synthesis and verification-related theorem proving, no benchmark has specifically targeted this fundamental bottleneck: automated VC proving. This work introduces Neural Theorem Proving for Verification Conditions (NTP4VC), presenting the first real-world multi-language benchmark for this task. From real-world projects such as Linux and Contiki-OS kernel, our benchmark leverages industrial pipelines (Why3 and Frama-C) to generate semantically equivalent test cases across formal languages of Isabelle, Lean, and Rocq. We evaluate large language models (LLMs), both general-purpose and those fine-tuned for theorem proving, on NTP4VC. Results indicate that although LLMs show promise in VC proving, significant challenges remain for program verification, highlighting a large gap and opportunity for future research.

Numina-Lean-Agent: An Open and General Agentic Reasoning System for Formal Mathematics

Agentic systems have recently become the dominant paradigm for formal theorem proving, achieving strong performance by coordinating multiple models and tools. However, existing approaches often rely on task-specific pipelines and trained formal provers, limiting their flexibility and reproducibility. In this paper, we propose the paradigm that directly uses a general coding agent as a formal math reasoner. This paradigm is motivated by (1) A general coding agent provides a natural interface for diverse reasoning tasks beyond proving, (2) Performance can be improved by simply replacing the underlying base model, without training, and (3) MCP enables flexible extension and autonomous calling of specialized tools, avoiding complex design. Based on this paradigm, we introduce Numina-Lean-Agent, which combines Claude Code with Numina-Lean-MCP to enable autonomous interaction with Lean, retrieval of relevant theorems, informal proving and auxiliary reasoning tools. Using Claude Opus 4.5 as the base model, Numina-Lean-Agent solves all problems in Putnam 2025 (12 / 12), matching the best closed-source system. Beyond benchmark evaluation, we further demonstrate its generality by interacting with mathematicians to successfully formalize the Brascamp-Lieb theorem. We release Numina-Lean-Agent and all solutions at https://github.com/project-numina/numina-lean-agent.

Coarse-to-Fine Hierarchical Alignment for UAV-based Human Detection using Diffusion Models

Training object detectors demands extensive, task-specific annotations, yet this requirement becomes impractical in UAV-based human detection due to constantly shifting target distributions and the scarcity of labeled images. As a remedy, synthetic simulators are adopted to generate annotated data, with a low annotation cost. However, the domain gap between synthetic and real images hinders the model from being effectively applied to the target domain. Accordingly, we introduce Coarse-to-Fine Hierarchical Alignment (CFHA), a three-stage diffusion-based framework designed to transform synthetic data for UAV-based human detection, narrowing the domain gap while preserving the original synthetic labels. CFHA explicitly decouples global style and local content domain discrepancies and bridges those gaps using three modules: (1) Global Style Transfer -- a diffusion model aligns color, illumination, and texture statistics of synthetic images to the realistic style, using only a small real reference set; (2) Local Refinement -- a super-resolution diffusion model is used to facilitate fine-grained and photorealistic details for the small objects, such as human instances, preserving shape and boundary integrity; (3) Hallucination Removal -- a module that filters out human instances whose visual attributes do not align with real-world data to make the human appearance closer to the target distribution. Extensive experiments on public UAV Sim2Real detection benchmarks demonstrate that our methods significantly improve the detection accuracy compared to the non-transformed baselines. Specifically, our method achieves up to $+14.1$ improvement of mAP50 on Semantic-Drone benchmark. Ablation studies confirm the complementary roles of the global and local stages and highlight the importance of hierarchical alignment. The code is released at \href{https://github.com/liwd190019/CFHA}{this url}.

PiCSAR: Probabilistic Confidence Selection And Ranking

Best-of-n sampling improves the accuracy of large language models (LLMs) and large reasoning models (LRMs) by generating multiple candidate solutions and selecting the one with the highest reward. The key challenge for reasoning tasks is designing a scoring function that can identify correct reasoning chains without access to ground-truth answers. We propose Probabilistic Confidence Selection And Ranking (PiCSAR): a simple, training-free method that scores each candidate generation using the joint log-likelihood of the reasoning and final answer. The joint log-likelihood of the reasoning and final answer naturally decomposes into reasoning confidence and answer confidence. PiCSAR achieves substantial gains across diverse benchmarks (+10.18 on MATH500, +9.81 on AIME2025), outperforming baselines with at least 2x fewer samples in 16 out of 20 comparisons. Our analysis reveals that correct reasoning chains exhibit significantly higher reasoning and answer confidence, justifying the effectiveness of PiCSAR.

APE-Bench I: Towards File-level Automated Proof Engineering of Formal Math Libraries

Recent progress in large language models (LLMs) has shown promise in formal theorem proving, yet existing benchmarks remain limited to isolated, static proof tasks, failing to capture the iterative, engineering-intensive workflows of real-world formal mathematics libraries. Motivated by analogous advances in software engineering, we introduce the paradigm of Automated Proof Engineering (APE), which aims to automate proof engineering tasks such as feature addition, proof refactoring, and bug fixing using LLMs. To facilitate research in this direction, we present APE-Bench I, the first realistic benchmark built from real-world commit histories of Mathlib4, featuring diverse file-level tasks described in natural language and verified via a hybrid approach combining the Lean compiler and LLM-as-a-Judge. We further develop Eleanstic, a scalable parallel verification infrastructure optimized for proof checking across multiple versions of Mathlib. Empirical results on state-of-the-art LLMs demonstrate strong performance on localized edits but substantial degradation on handling complex proof engineering. This work lays the foundation for developing agentic workflows in proof engineering, with future benchmarks targeting multi-file coordination, project-scale verification, and autonomous agents capable of planning, editing, and repairing formal libraries.

Theorem Prover as a Judge for Synthetic Data Generation

The demand for synthetic data in mathematical reasoning has increased due to its potential to enhance the mathematical capabilities of large language models (LLMs). However, ensuring the validity of intermediate reasoning steps remains a significant challenge, affecting data quality. While formal verification via theorem provers effectively validates LLM reasoning, the autoformalisation of mathematical proofs remains error-prone. In response, we introduce iterative autoformalisation, an approach that iteratively refines theorem prover formalisation to mitigate errors, thereby increasing the execution rate on the Lean prover from 60% to 87%. Building upon that, we introduce Theorem Prover as a Judge (TP-as-a-Judge), a method that employs theorem prover formalisation to rigorously assess LLM intermediate reasoning, effectively integrating autoformalisation with synthetic data generation. Finally, we present Reinforcement Learning from Theorem Prover Feedback (RLTPF), a framework that replaces human annotation with theorem prover feedback in Reinforcement Learning from Human Feedback (RLHF). Across multiple LLMs, applying TP-as-a-Judge and RLTPF improves benchmarks with only 3,508 samples, achieving 5.56% accuracy gain on Mistral-7B for MultiArith, 6.00% on Llama-2-7B for SVAMP, and 3.55% on Llama-3.1-8B for AQUA.

Formal Mathematical Reasoning: A New Frontier in AI

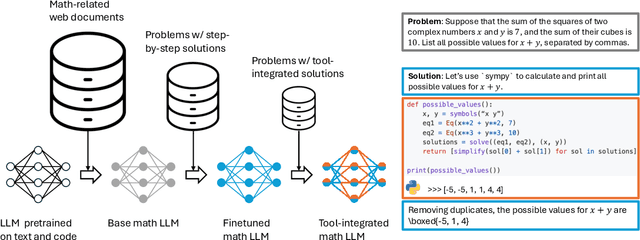
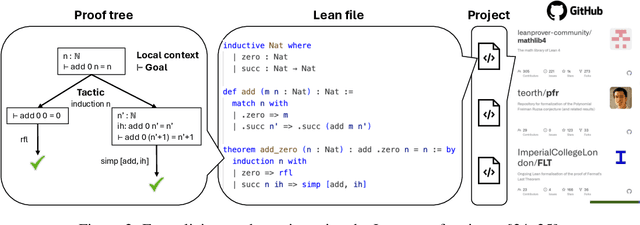
AI for Mathematics (AI4Math) is not only intriguing intellectually but also crucial for AI-driven discovery in science, engineering, and beyond. Extensive efforts on AI4Math have mirrored techniques in NLP, in particular, training large language models on carefully curated math datasets in text form. As a complementary yet less explored avenue, formal mathematical reasoning is grounded in formal systems such as proof assistants, which can verify the correctness of reasoning and provide automatic feedback. In this position paper, we advocate for formal mathematical reasoning and argue that it is indispensable for advancing AI4Math to the next level. In recent years, we have seen steady progress in using AI to perform formal reasoning, including core tasks such as theorem proving and autoformalization, as well as emerging applications such as verifiable generation of code and hardware designs. However, significant challenges remain to be solved for AI to truly master mathematics and achieve broader impact. We summarize existing progress, discuss open challenges, and envision critical milestones to measure future success. At this inflection point for formal mathematical reasoning, we call on the research community to come together to drive transformative advancements in this field.

End-to-End Ontology Learning with Large Language Models

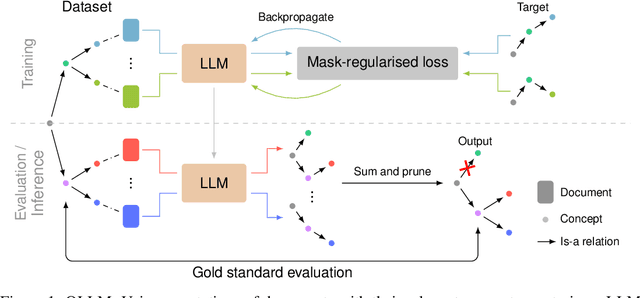
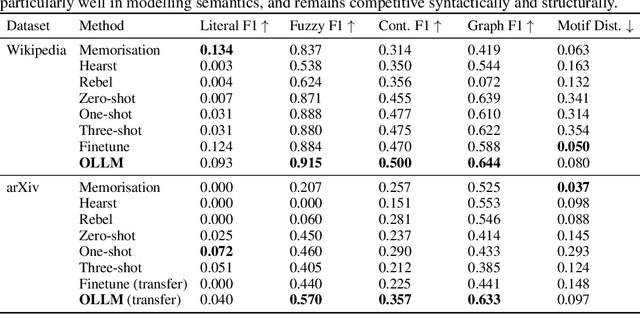
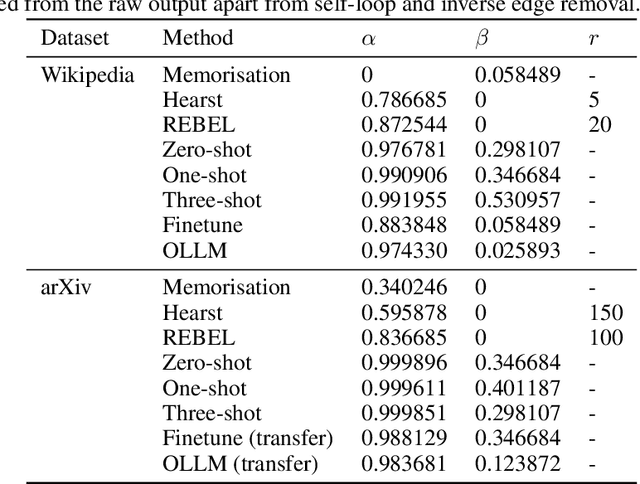
Ontologies are useful for automatic machine processing of domain knowledge as they represent it in a structured format. Yet, constructing ontologies requires substantial manual effort. To automate part of this process, large language models (LLMs) have been applied to solve various subtasks of ontology learning. However, this partial ontology learning does not capture the interactions between subtasks. We address this gap by introducing OLLM, a general and scalable method for building the taxonomic backbone of an ontology from scratch. Rather than focusing on subtasks, like individual relations between entities, we model entire subcomponents of the target ontology by finetuning an LLM with a custom regulariser that reduces overfitting on high-frequency concepts. We introduce a novel suite of metrics for evaluating the quality of the generated ontology by measuring its semantic and structural similarity to the ground truth. In contrast to standard metrics, our metrics use deep learning techniques to define more robust distance measures between graphs. Both our quantitative and qualitative results on Wikipedia show that OLLM outperforms subtask composition methods, producing more semantically accurate ontologies while maintaining structural integrity. We further demonstrate that our model can be effectively adapted to new domains, like arXiv, needing only a small number of training examples. Our source code and datasets are available at https://github.com/andylolu2/ollm.

Shallow Diffuse: Robust and Invisible Watermarking through Low-Dimensional Subspaces in Diffusion Models

The widespread use of AI-generated content from diffusion models has raised significant concerns regarding misinformation and copyright infringement. Watermarking is a crucial technique for identifying these AI-generated images and preventing their misuse. In this paper, we introduce Shallow Diffuse, a new watermarking technique that embeds robust and invisible watermarks into diffusion model outputs. Unlike existing approaches that integrate watermarking throughout the entire diffusion sampling process, Shallow Diffuse decouples these steps by leveraging the presence of a low-dimensional subspace in the image generation process. This method ensures that a substantial portion of the watermark lies in the null space of this subspace, effectively separating it from the image generation process. Our theoretical and empirical analyses show that this decoupling strategy greatly enhances the consistency of data generation and the detectability of the watermark. Extensive experiments further validate that our Shallow Diffuse outperforms existing watermarking methods in terms of robustness and consistency. The codes will be released at https://github.com/liwd190019/Shallow-Diffuse.

Learning a Mini-batch Graph Transformer via Two-stage Interaction Augmentation

Mini-batch Graph Transformer (MGT), as an emerging graph learning model, has demonstrated significant advantages in semi-supervised node prediction tasks with improved computational efficiency and enhanced model robustness. However, existing methods for processing local information either rely on sampling or simple aggregation, which respectively result in the loss and squashing of critical neighbor information.Moreover, the limited number of nodes in each mini-batch restricts the model's capacity to capture the global characteristic of the graph. In this paper, we propose LGMformer, a novel MGT model that employs a two-stage augmented interaction strategy, transitioning from local to global perspectives, to address the aforementioned bottlenecks.The local interaction augmentation (LIA) presents a neighbor-target interaction Transformer (NTIformer) to acquire an insightful understanding of the co-interaction patterns between neighbors and the target node, resulting in a locally effective token list that serves as input for the MGT. In contrast, global interaction augmentation (GIA) adopts a cross-attention mechanism to incorporate entire graph prototypes into the target node epresentation, thereby compensating for the global graph information to ensure a more comprehensive perception. To this end, LGMformer achieves the enhancement of node representations under the MGT paradigm.Experimental results related to node classification on the ten benchmark datasets demonstrate the effectiveness of the proposed method. Our code is available at https://github.com/l-wd/LGMformer.