Teaching Transformers Modular Arithmetic at Scale

Modular addition is, on its face, a simple operation: given $N$ elements in $\mathbb{Z}_q$, compute their sum modulo $q$. Yet, scalable machine learning solutions to this problem remain elusive: prior work trains ML models that sum $N \le 6$ elements mod $q \le 1000$. Promising applications of ML models for cryptanalysis-which often involve modular arithmetic with large $N$ and $q$-motivate reconsideration of this problem. This work proposes three changes to the modular addition model training pipeline: more diverse training data, an angular embedding, and a custom loss function. With these changes, we demonstrate success with our approach for $N = 256, q = 3329$, a case which is interesting for cryptographic applications, and a significant increase in $N$ and $q$ over prior work. These techniques also generalize to other modular arithmetic problems, motivating future work.

Machine learning for modular multiplication

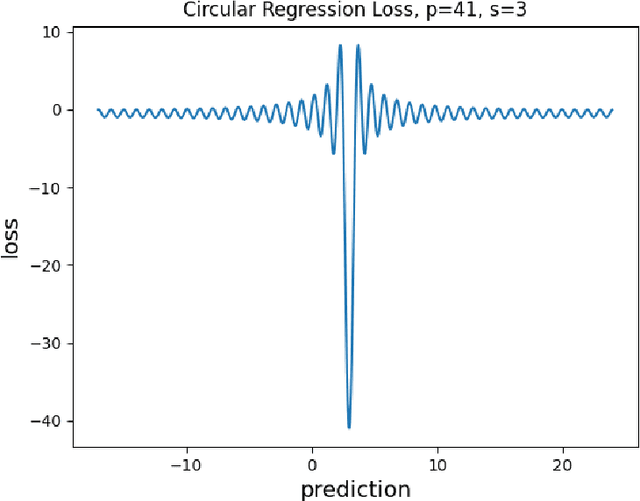
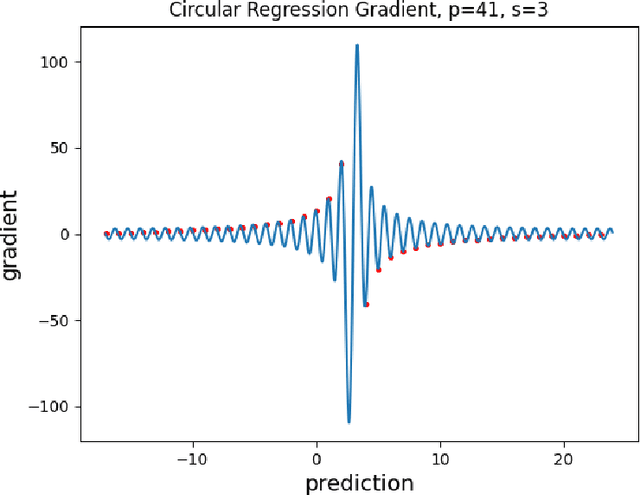
Motivated by cryptographic applications, we investigate two machine learning approaches to modular multiplication: namely circular regression and a sequence-to-sequence transformer model. The limited success of both methods demonstrated in our results gives evidence for the hardness of tasks involving modular multiplication upon which cryptosystems are based.

Salsa Fresca: Angular Embeddings and Pre-Training for ML Attacks on Learning With Errors

Learning with Errors (LWE) is a hard math problem underlying recently standardized post-quantum cryptography (PQC) systems for key exchange and digital signatures. Prior work proposed new machine learning (ML)-based attacks on LWE problems with small, sparse secrets, but these attacks require millions of LWE samples to train on and take days to recover secrets. We propose three key methods -- better preprocessing, angular embeddings and model pre-training -- to improve these attacks, speeding up preprocessing by $25\times$ and improving model sample efficiency by $10\times$. We demonstrate for the first time that pre-training improves and reduces the cost of ML attacks on LWE. Our architecture improvements enable scaling to larger-dimension LWE problems: this work is the first instance of ML attacks recovering sparse binary secrets in dimension $n=1024$, the smallest dimension used in practice for homomorphic encryption applications of LWE where sparse binary secrets are proposed.

SALSA PICANTE: a machine learning attack on LWE with binary secrets

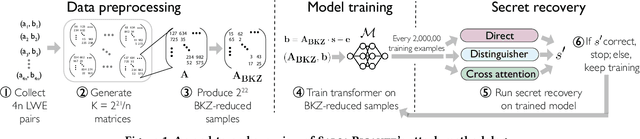
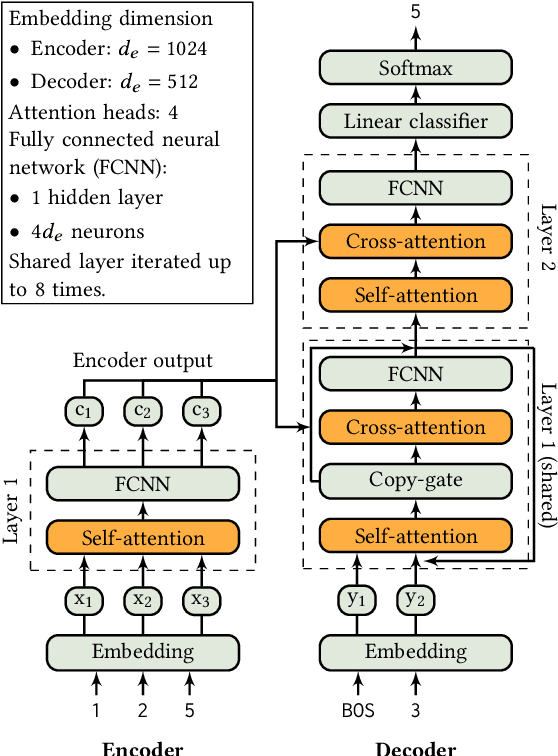
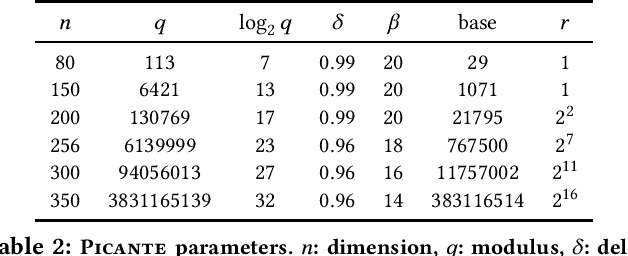
The Learning With Errors (LWE) problem is one of the major hard problems in post-quantum cryptography. For example, 1) the only Key Exchange Mechanism KEM standardized by NIST [14] is based on LWE; and 2) current publicly available Homomorphic Encryption (HE) libraries are based on LWE. NIST KEM schemes use random secrets, but homomorphic encryption schemes use binary or ternary secrets, for efficiency reasons. In particular, sparse binary secrets have been proposed, but not standardized [2], for HE. Prior work SALSA [49] demonstrated a new machine learning attack on sparse binary secrets for the LWE problem in small dimensions (up to n = 128) and low Hamming weights (up to h = 4). However, this attack assumed access to millions of LWE samples, and was not scaled to higher Hamming weights or dimensions. Our attack, PICANTE, reduces the number of samples required to just m = 4n samples. Moreover, it can recover secrets with much larger dimensions (up to 350) and Hamming weights (roughly n/10, or h = 33 for n = 300). To achieve this, we introduce a preprocessing step which allows us to generate the training data from a linear number of samples and changes the distribution of the training data to improve transformer training. We also improve the distinguisher/secret recovery methods of SALSA and introduce a novel cross-attention recovery mechanism which allows us to read-off the secret directly from the trained models.

SALSA: Attacking Lattice Cryptography with Transformers

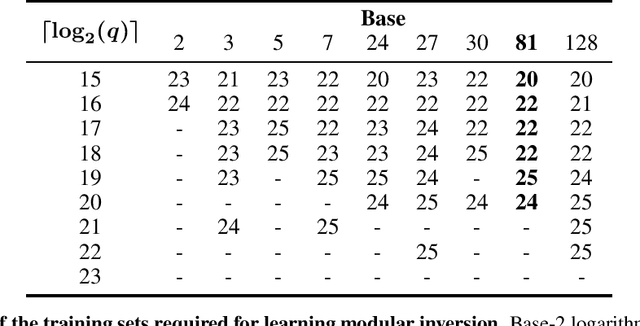
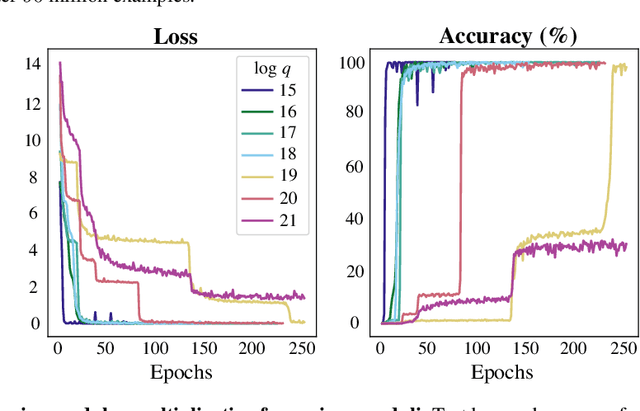
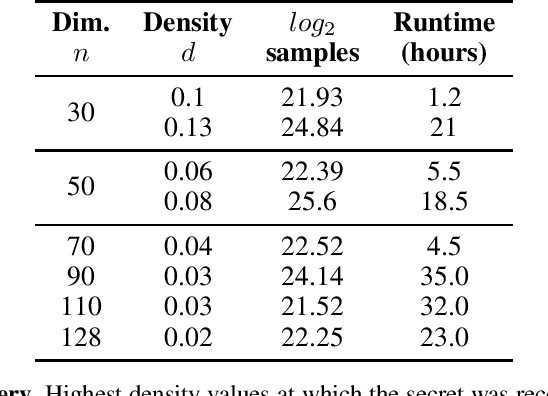
Currently deployed public-key cryptosystems will be vulnerable to attacks by full-scale quantum computers. Consequently, "quantum resistant" cryptosystems are in high demand, and lattice-based cryptosystems, based on a hard problem known as Learning With Errors (LWE), have emerged as strong contenders for standardization. In this work, we train transformers to perform modular arithmetic and combine half-trained models with statistical cryptanalysis techniques to propose SALSA: a machine learning attack on LWE-based cryptographic schemes. SALSA can fully recover secrets for small-to-mid size LWE instances with sparse binary secrets, and may scale to attack real-world LWE-based cryptosystems.

Transparency Tools for Fairness in AI (Luskin)

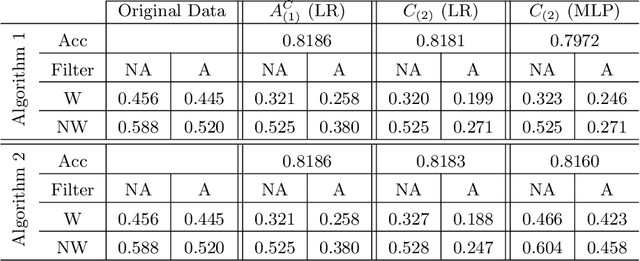
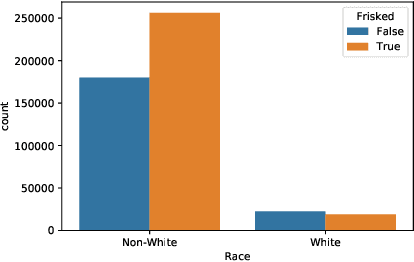
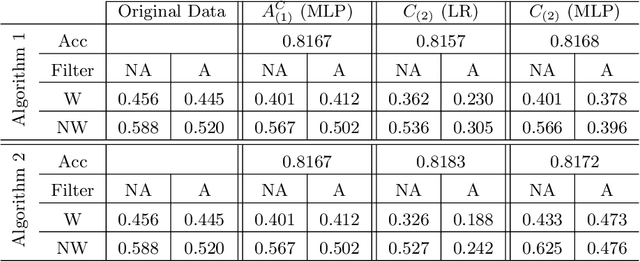
We propose new tools for policy-makers to use when assessing and correcting fairness and bias in AI algorithms. The three tools are: - A new definition of fairness called "controlled fairness" with respect to choices of protected features and filters. The definition provides a simple test of fairness of an algorithm with respect to a dataset. This notion of fairness is suitable in cases where fairness is prioritized over accuracy, such as in cases where there is no "ground truth" data, only data labeled with past decisions (which may have been biased). - Algorithms for retraining a given classifier to achieve "controlled fairness" with respect to a choice of features and filters. Two algorithms are presented, implemented and tested. These algorithms require training two different models in two stages. We experiment with combinations of various types of models for the first and second stage and report on which combinations perform best in terms of fairness and accuracy. - Algorithms for adjusting model parameters to achieve a notion of fairness called "classification parity". This notion of fairness is suitable in cases where accuracy is prioritized. Two algorithms are presented, one which assumes that protected features are accessible to the model during testing, and one which assumes protected features are not accessible during testing. We evaluate our tools on three different publicly available datasets. We find that the tools are useful for understanding various dimensions of bias, and that in practice the algorithms are effective in starkly reducing a given observed bias when tested on new data.

CHET: Compiler and Runtime for Homomorphic Evaluation of Tensor Programs

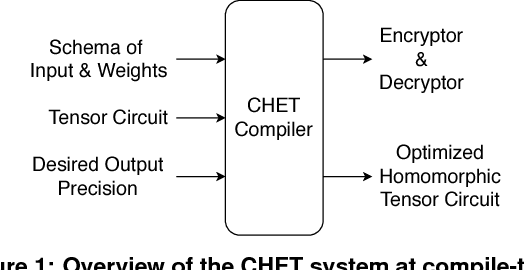
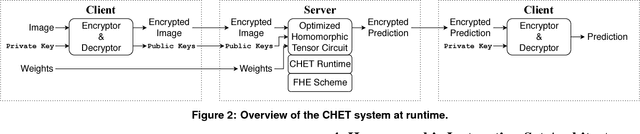
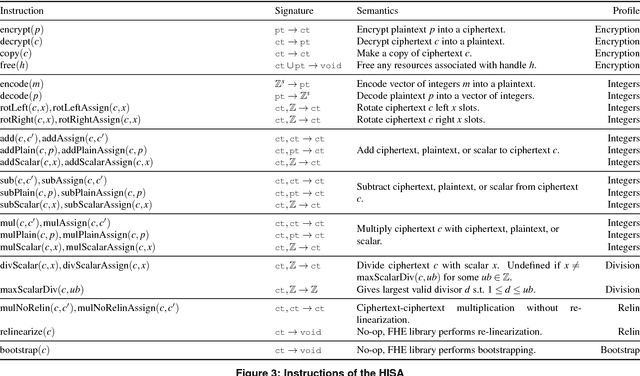
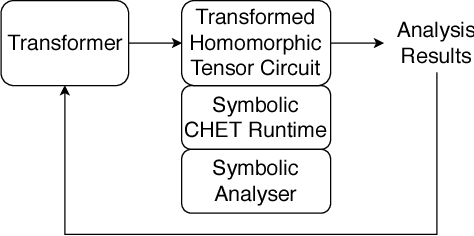
Fully Homomorphic Encryption (FHE) refers to a set of encryption schemes that allow computations to be applied directly on encrypted data without requiring a secret key. This enables novel application scenarios where a client can safely offload storage and computation to a third-party cloud provider without having to trust the software and the hardware vendors with the decryption keys. Recent advances in both FHE schemes and implementations have moved such applications from theoretical possibilities into the realm of practicalities. This paper proposes a compact and well-reasoned interface called the Homomorphic Instruction Set Architecture (HISA) for developing FHE applications. Just as the hardware ISA interface enabled hardware advances to proceed independent of software advances in the compiler and language runtimes, HISA decouples compiler optimizations and runtimes for supporting FHE applications from advancements in the underlying FHE schemes. This paper demonstrates the capabilities of HISA by building an end-to-end software stack for evaluating neural network models on encrypted data. Our stack includes an end-to-end compiler, runtime, and a set of optimizations. Our approach shows generated code, on a set of popular neural network architectures, is faster than hand-optimized implementations.

Crypto-Nets: Neural Networks over Encrypted Data

The problem we address is the following: how can a user employ a predictive model that is held by a third party, without compromising private information. For example, a hospital may wish to use a cloud service to predict the readmission risk of a patient. However, due to regulations, the patient's medical files cannot be revealed. The goal is to make an inference using the model, without jeopardizing the accuracy of the prediction or the privacy of the data. To achieve high accuracy, we use neural networks, which have been shown to outperform other learning models for many tasks. To achieve the privacy requirements, we use homomorphic encryption in the following protocol: the data owner encrypts the data and sends the ciphertexts to the third party to obtain a prediction from a trained model. The model operates on these ciphertexts and sends back the encrypted prediction. In this protocol, not only the data remains private, even the values predicted are available only to the data owner. Using homomorphic encryption and modifications to the activation functions and training algorithms of neural networks, we show that it is protocol is possible and may be feasible. This method paves the way to build a secure cloud-based neural network prediction services without invading users' privacy.