STLight: a Fully Convolutional Approach for Efficient Predictive Learning by Spatio-Temporal joint Processing

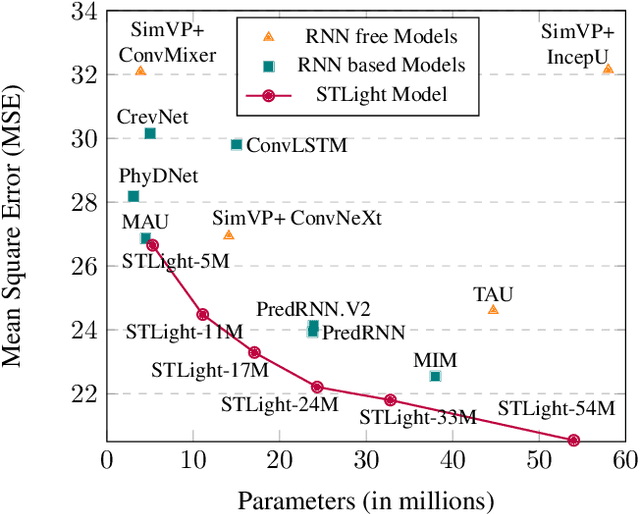
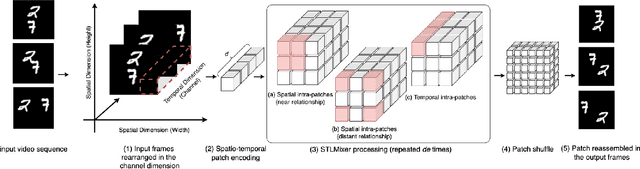
Spatio-Temporal predictive Learning is a self-supervised learning paradigm that enables models to identify spatial and temporal patterns by predicting future frames based on past frames. Traditional methods, which use recurrent neural networks to capture temporal patterns, have proven their effectiveness but come with high system complexity and computational demand. Convolutions could offer a more efficient alternative but are limited by their characteristic of treating all previous frames equally, resulting in poor temporal characterization, and by their local receptive field, limiting the capacity to capture distant correlations among frames. In this paper, we propose STLight, a novel method for spatio-temporal learning that relies solely on channel-wise and depth-wise convolutions as learnable layers. STLight overcomes the limitations of traditional convolutional approaches by rearranging spatial and temporal dimensions together, using a single convolution to mix both types of features into a comprehensive spatio-temporal patch representation. This representation is then processed in a purely convolutional framework, capable of focusing simultaneously on the interaction among near and distant patches, and subsequently allowing for efficient reconstruction of the predicted frames. Our architecture achieves state-of-the-art performance on STL benchmarks across different datasets and settings, while significantly improving computational efficiency in terms of parameters and computational FLOPs. The code is publicly available

Global Lyapunov functions: a long-standing open problem in mathematics, with symbolic transformers

Despite their spectacular progress, language models still struggle on complex reasoning tasks, such as advanced mathematics. We consider a long-standing open problem in mathematics: discovering a Lyapunov function that ensures the global stability of a dynamical system. This problem has no known general solution, and algorithmic solvers only exist for some small polynomial systems. We propose a new method for generating synthetic training samples from random solutions, and show that sequence-to-sequence transformers trained on such datasets perform better than algorithmic solvers and humans on polynomial systems, and can discover new Lyapunov functions for non-polynomial systems.

Teaching Transformers Modular Arithmetic at Scale

Modular addition is, on its face, a simple operation: given $N$ elements in $\mathbb{Z}_q$, compute their sum modulo $q$. Yet, scalable machine learning solutions to this problem remain elusive: prior work trains ML models that sum $N \le 6$ elements mod $q \le 1000$. Promising applications of ML models for cryptanalysis-which often involve modular arithmetic with large $N$ and $q$-motivate reconsideration of this problem. This work proposes three changes to the modular addition model training pipeline: more diverse training data, an angular embedding, and a custom loss function. With these changes, we demonstrate success with our approach for $N = 256, q = 3329$, a case which is interesting for cryptographic applications, and a significant increase in $N$ and $q$ over prior work. These techniques also generalize to other modular arithmetic problems, motivating future work.