Global Lyapunov functions: a long-standing open problem in mathematics, with symbolic transformers

Despite their spectacular progress, language models still struggle on complex reasoning tasks, such as advanced mathematics. We consider a long-standing open problem in mathematics: discovering a Lyapunov function that ensures the global stability of a dynamical system. This problem has no known general solution, and algorithmic solvers only exist for some small polynomial systems. We propose a new method for generating synthetic training samples from random solutions, and show that sequence-to-sequence transformers trained on such datasets perform better than algorithmic solvers and humans on polynomial systems, and can discover new Lyapunov functions for non-polynomial systems.

HyperTree Proof Search for Neural Theorem Proving

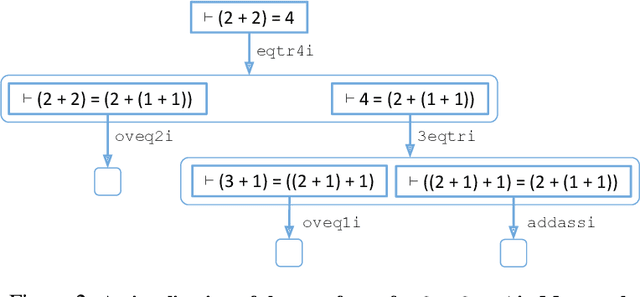
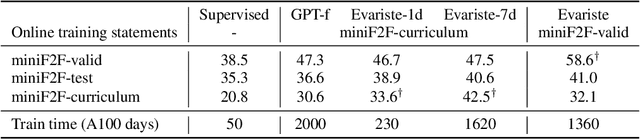
We propose an online training procedure for a transformer-based automated theorem prover. Our approach leverages a new search algorithm, HyperTree Proof Search (HTPS), inspired by the recent success of AlphaZero. Our model learns from previous proof searches through online training, allowing it to generalize to domains far from the training distribution. We report detailed ablations of our pipeline's main components by studying performance on three environments of increasing complexity. In particular, we show that with HTPS alone, a model trained on annotated proofs manages to prove 65.4% of a held-out set of Metamath theorems, significantly outperforming the previous state of the art of 56.5% by GPT-f. Online training on these unproved theorems increases accuracy to 82.6%. With a similar computational budget, we improve the state of the art on the Lean-based miniF2F-curriculum dataset from 31% to 42% proving accuracy.

A deep language model to predict metabolic network equilibria

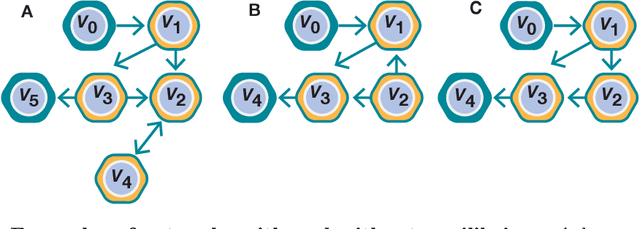
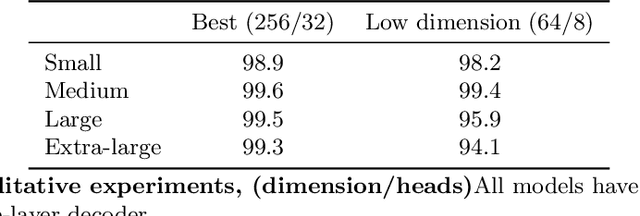
We show that deep learning models, and especially architectures like the Transformer, originally intended for natural language, can be trained on randomly generated datasets to predict to very high accuracy both the qualitative and quantitative features of metabolic networks. Using standard mathematical techniques, we create large sets (40 million elements) of random networks that can be used to train our models. These trained models can predict network equilibrium on random graphs in more than 99% of cases. They can also generalize to graphs with different structure than those encountered at training. Finally, they can predict almost perfectly the equilibria of a small set of known biological networks. Our approach is both very economical in experimental data and uses only small and shallow deep-learning model, far from the large architectures commonly used in machine translation. Such results pave the way for larger use of deep learning models for problems related to biological networks in key areas such as quantitative systems pharmacology, systems biology, and synthetic biology.

Deep Differential System Stability -- Learning advanced computations from examples

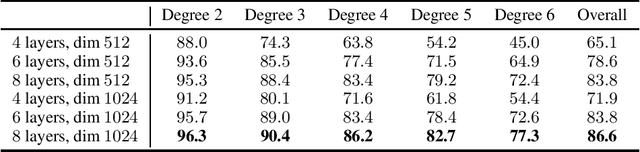
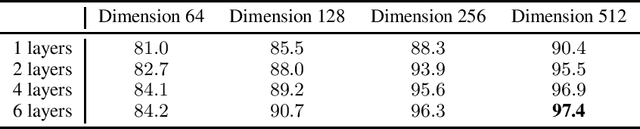
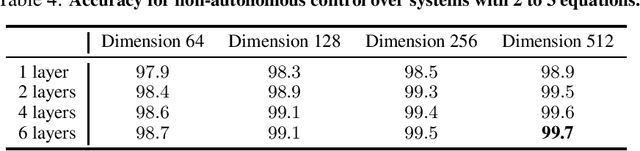
Can advanced mathematical computations be learned from examples? Using transformers over large generated datasets, we train models to learn properties of differential systems, such as local stability, behavior at infinity and controllability. We achieve near perfect estimates of qualitative characteristics of the systems, and good approximations of numerical quantities, demonstrating that neural networks can learn advanced theorems and complex computations without built-in mathematical knowledge.