Extrapolating Jet Radiation with Autoregressive Transformers

Generative networks are an exciting tool for fast LHC event generation. Usually, they are used to generate configurations with a fixed number of particles. Autoregressive transformers allow us to generate events with variable numbers of particles, very much in line with the physics of QCD jet radiation. We show how they can learn a factorized likelihood for jet radiation and extrapolate in terms of the number of generated jets. For this extrapolation, bootstrapping training data and training with modifications of the likelihood loss can be used.

PatternBoost: Constructions in Mathematics with a Little Help from AI

We introduce PatternBoost, a flexible method for finding interesting constructions in mathematics. Our algorithm alternates between two phases. In the first ``local'' phase, a classical search algorithm is used to produce many desirable constructions. In the second ``global'' phase, a transformer neural network is trained on the best such constructions. Samples from the trained transformer are then used as seeds for the first phase, and the process is repeated. We give a detailed introduction to this technique, and discuss the results of its application to several problems in extremal combinatorics. The performance of PatternBoost varies across different problems, but there are many situations where its performance is quite impressive. Using our technique, we find the best known solutions to several long-standing problems, including the construction of a counterexample to a conjecture that had remained open for 30 years.

Global Lyapunov functions: a long-standing open problem in mathematics, with symbolic transformers

Despite their spectacular progress, language models still struggle on complex reasoning tasks, such as advanced mathematics. We consider a long-standing open problem in mathematics: discovering a Lyapunov function that ensures the global stability of a dynamical system. This problem has no known general solution, and algorithmic solvers only exist for some small polynomial systems. We propose a new method for generating synthetic training samples from random solutions, and show that sequence-to-sequence transformers trained on such datasets perform better than algorithmic solvers and humans on polynomial systems, and can discover new Lyapunov functions for non-polynomial systems.

Emergent properties with repeated examples

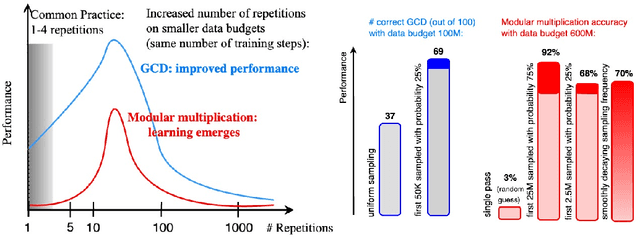
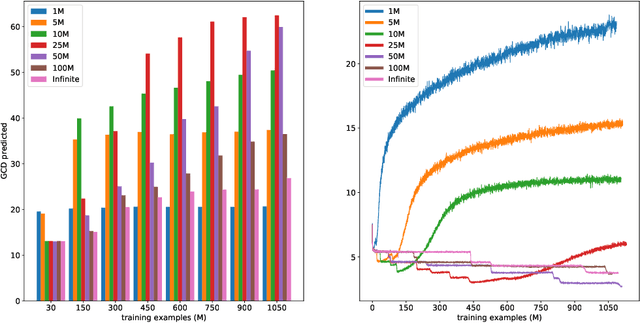
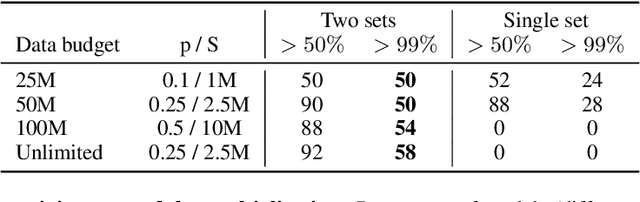
We study the performance of transformers as a function of the number of repetitions of training examples with algorithmically generated datasets. On three problems of mathematics: the greatest common divisor, modular multiplication, and matrix eigenvalues, we show that for a fixed number of training steps, models trained on smaller sets of repeated examples outperform models trained on larger sets of single-use examples. We also demonstrate that two-set training - repeated use of a small random subset of examples, along normal sampling on the rest of the training set - provides for faster learning and better performance. This highlights that the benefits of repetition can outweigh those of data diversity. These datasets and problems provide a controlled setting to shed light on the still poorly understood interplay between generalization and memorization in deep learning.

Transforming the Bootstrap: Using Transformers to Compute Scattering Amplitudes in Planar N = 4 Super Yang-Mills Theory

We pursue the use of deep learning methods to improve state-of-the-art computations in theoretical high-energy physics. Planar N = 4 Super Yang-Mills theory is a close cousin to the theory that describes Higgs boson production at the Large Hadron Collider; its scattering amplitudes are large mathematical expressions containing integer coefficients. In this paper, we apply Transformers to predict these coefficients. The problem can be formulated in a language-like representation amenable to standard cross-entropy training objectives. We design two related experiments and show that the model achieves high accuracy (> 98%) on both tasks. Our work shows that Transformers can be applied successfully to problems in theoretical physics that require exact solutions.

Salsa Fresca: Angular Embeddings and Pre-Training for ML Attacks on Learning With Errors

Learning with Errors (LWE) is a hard math problem underlying recently standardized post-quantum cryptography (PQC) systems for key exchange and digital signatures. Prior work proposed new machine learning (ML)-based attacks on LWE problems with small, sparse secrets, but these attacks require millions of LWE samples to train on and take days to recover secrets. We propose three key methods -- better preprocessing, angular embeddings and model pre-training -- to improve these attacks, speeding up preprocessing by $25\times$ and improving model sample efficiency by $10\times$. We demonstrate for the first time that pre-training improves and reduces the cost of ML attacks on LWE. Our architecture improvements enable scaling to larger-dimension LWE problems: this work is the first instance of ML attacks recovering sparse binary secrets in dimension $n=1024$, the smallest dimension used in practice for homomorphic encryption applications of LWE where sparse binary secrets are proposed.

Can transformers learn the greatest common divisor?

I investigate the capability of small transformers to compute the greatest common divisor (GCD) of two positive integers. When the training distribution and the representation base are carefully chosen, models achieve 98% accuracy and correctly predict 91 of the 100 first GCD. Model predictions are deterministic and fully interpretable. During training, the models learn to cluster input pairs with the same GCD, and classify them by their divisors. Basic models, trained from uniform operands encoded on small bases, only compute a handful of GCD (up to 38 out of 100): the products of divisors of the base. Longer training and larger bases allow some models to "grok" small prime GCD. Training from log-uniform operands boosts performance to 73 correct GCD, and balancing the training distribution of GCD, from inverse square to log-uniform, to 91 GCD. Training models from a uniform distribution of GCD breaks the deterministic model behavior.

Length Generalization in Arithmetic Transformers

We examine how transformers cope with two challenges: learning basic integer arithmetic, and generalizing to longer sequences than seen during training. We find that relative position embeddings enable length generalization for simple tasks, such as addition: models trained on $5$-digit numbers can perform $15$-digit sums. However, this method fails for multiplication, and we propose train set priming: adding a few ($10$ to $50$) long sequences to the training set. We show that priming allows models trained on $5$-digit $\times$ $3$-digit multiplications to generalize to $35\times 3$ examples. We also show that models can be primed for different generalization lengths, and that the priming sample size scales as the logarithm of the training set size. Finally, we discuss potential applications of priming beyond arithmetic.

Contrastive Distillation Is a Sample-Efficient Self-Supervised Loss Policy for Transfer Learning

Traditional approaches to RL have focused on learning decision policies directly from episodic decisions, while slowly and implicitly learning the semantics of compositional representations needed for generalization. While some approaches have been adopted to refine representations via auxiliary self-supervised losses while simultaneously learning decision policies, learning compositional representations from hand-designed and context-independent self-supervised losses (multi-view) still adapts relatively slowly to the real world, which contains many non-IID subspaces requiring rapid distribution shift in both time and spatial attention patterns at varying levels of abstraction. In contrast, supervised language model cascades have shown the flexibility to adapt to many diverse manifolds, and hints of self-learning needed for autonomous task transfer. However, to date, transfer methods for language models like few-shot learning and fine-tuning still require human supervision and transfer learning using self-learning methods has been underexplored. We propose a self-supervised loss policy called contrastive distillation which manifests latent variables with high mutual information with both source and target tasks from weights to tokens. We show how this outperforms common methods of transfer learning and suggests a useful design axis of trading off compute for generalizability for online transfer. Contrastive distillation is improved through sampling from memory and suggests a simple algorithm for more efficiently sampling negative examples for contrastive losses than random sampling.

What is my math transformer doing? -- Three results on interpretability and generalization

This paper investigates the failure cases and out-of-distribution behavior of transformers trained on matrix inversion and eigenvalue decomposition. I show that incorrect model predictions still retain deep mathematical properties of the solution (e.g. correct eigenvalues, unit norm of eigenvectors), and that almost all model failures can be attributed to, and predicted from, properties of the problem or solution. This demonstrates that, when in doubt, math transformers do not hallucinate absurd solutions (as was sometimes proposed) but remain ``roughly right''. I also show that the careful choice of a training dataset can accelerate training, while allowing the model to generalize out of its training distribution, invalidating the idea that transformers ``merely interpolate'' from memorized examples.