Meta-Designing Quantum Experiments with Language Models

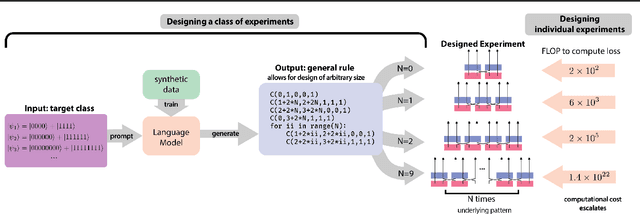
Artificial Intelligence (AI) has the potential to significantly advance scientific discovery by finding solutions beyond human capabilities. However, these super-human solutions are often unintuitive and require considerable effort to uncover underlying principles, if possible at all. Here, we show how a code-generating language model trained on synthetic data can not only find solutions to specific problems but can create meta-solutions, which solve an entire class of problems in one shot and simultaneously offer insight into the underlying design principles. Specifically, for the design of new quantum physics experiments, our sequence-to-sequence transformer architecture generates interpretable Python code that describes experimental blueprints for a whole class of quantum systems. We discover general and previously unknown design rules for infinitely large classes of quantum states. The ability to automatically generate generalized patterns in readable computer code is a crucial step toward machines that help discover new scientific understanding -- one of the central aims of physics.

Don't Trust: Verify -- Grounding LLM Quantitative Reasoning with Autoformalization

Large language models (LLM), such as Google's Minerva and OpenAI's GPT families, are becoming increasingly capable of solving mathematical quantitative reasoning problems. However, they still make unjustified logical and computational errors in their reasoning steps and answers. In this paper, we leverage the fact that if the training corpus of LLMs contained sufficiently many examples of formal mathematics (e.g. in Isabelle, a formal theorem proving environment), they can be prompted to translate i.e. autoformalize informal mathematical statements into formal Isabelle code -- which can be verified automatically for internal consistency. This provides a mechanism to automatically reject solutions whose formalized versions are inconsistent within themselves or with the formalized problem statement. We evaluate our method on GSM8K, MATH and MultiArith datasets and demonstrate that our approach provides a consistently better heuristic than vanilla majority voting -- the previously best method to identify correct answers, by more than 12% on GSM8K. In our experiments it improves results consistently across all datasets and LLM model sizes. The code can be found at https://github.com/jinpz/dtv.

REFACTOR: Learning to Extract Theorems from Proofs

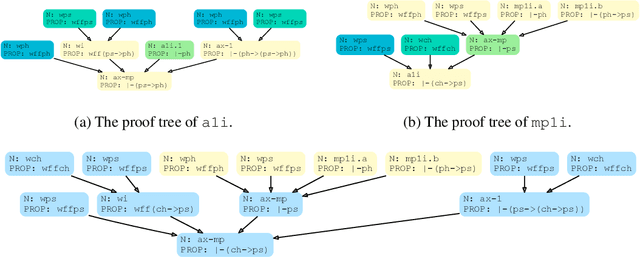
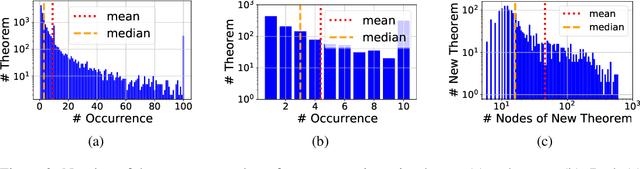
Human mathematicians are often good at recognizing modular and reusable theorems that make complex mathematical results within reach. In this paper, we propose a novel method called theoREm-from-prooF extrACTOR (REFACTOR) for training neural networks to mimic this ability in formal mathematical theorem proving. We show on a set of unseen proofs, REFACTOR is able to extract 19.6% of the theorems that humans would use to write the proofs. When applying the model to the existing Metamath library, REFACTOR extracted 16 new theorems. With newly extracted theorems, we show that the existing proofs in the MetaMath database can be refactored. The new theorems are used very frequently after refactoring, with an average usage of 733.5 times, and help shorten the proof lengths. Lastly, we demonstrate that the prover trained on the new-theorem refactored dataset proves more test theorems and outperforms state-of-the-art baselines by frequently leveraging a diverse set of newly extracted theorems. Code can be found at https://github.com/jinpz/refactor.

Focused Transformer: Contrastive Training for Context Scaling

Large language models have an exceptional capability to incorporate new information in a contextual manner. However, the full potential of such an approach is often restrained due to a limitation in the effective context length. One solution to this issue is to endow an attention layer with access to an external memory, which comprises of (key, value) pairs. Yet, as the number of documents increases, the proportion of relevant keys to irrelevant ones decreases, leading the model to focus more on the irrelevant keys. We identify a significant challenge, dubbed the distraction issue, where keys linked to different semantic values might overlap, making them hard to distinguish. To tackle this problem, we introduce the Focused Transformer (FoT), a technique that employs a training process inspired by contrastive learning. This novel approach enhances the structure of the (key, value) space, enabling an extension of the context length. Our method allows for fine-tuning pre-existing, large-scale models to lengthen their effective context. This is demonstrated by our fine-tuning of $3B$ and $7B$ OpenLLaMA checkpoints. The resulting models, which we name LongLLaMA, exhibit advancements in tasks requiring a long context. We further illustrate that our LongLLaMA models adeptly manage a $256 k$ context length for passkey retrieval.

Length Generalization in Arithmetic Transformers

We examine how transformers cope with two challenges: learning basic integer arithmetic, and generalizing to longer sequences than seen during training. We find that relative position embeddings enable length generalization for simple tasks, such as addition: models trained on $5$-digit numbers can perform $15$-digit sums. However, this method fails for multiplication, and we propose train set priming: adding a few ($10$ to $50$) long sequences to the training set. We show that priming allows models trained on $5$-digit $\times$ $3$-digit multiplications to generalize to $35\times 3$ examples. We also show that models can be primed for different generalization lengths, and that the priming sample size scales as the logarithm of the training set size. Finally, we discuss potential applications of priming beyond arithmetic.

Evaluating Language Models for Mathematics through Interactions

The standard methodology of evaluating large language models (LLMs) based on static pairs of inputs and outputs is insufficient for developing assistants: this kind of assessments fails to take into account the essential interactive element in their deployment, and therefore limits how we understand language model capabilities. We introduce CheckMate, an adaptable prototype platform for humans to interact with and evaluate LLMs. We conduct a study with CheckMate to evaluate three language models~(InstructGPT, ChatGPT, and GPT-4) as assistants in proving undergraduate-level mathematics, with a mixed cohort of participants from undergraduate students to professors of mathematics. We release the resulting interaction and rating dataset, MathConverse. By analysing MathConverse, we derive a preliminary taxonomy of human behaviours and uncover that despite a generally positive correlation, there are notable instances of divergence between correctness and perceived helpfulness in LLM generations, amongst other findings. Further, we identify useful scenarios and existing issues of GPT-4 in mathematical reasoning through a series of case studies contributed by expert mathematicians. We conclude with actionable takeaways for ML practitioners and mathematicians: models which communicate uncertainty, respond well to user corrections, are more interpretable and concise may constitute better assistants; interactive evaluation is a promising way to continually navigate the capability of these models; humans should be aware of language models' algebraic fallibility, and for that reason discern where they should be used.

Lexinvariant Language Models

Token embeddings, a mapping from discrete lexical symbols to continuous vectors, are at the heart of any language model (LM). However, lexical symbol meanings can also be determined and even redefined by their structural role in a long context. In this paper, we ask: is it possible for a language model to be performant without \emph{any} fixed token embeddings? Such a language model would have to rely entirely on the co-occurence and repetition of tokens in the context rather than the \textit{a priori} identity of any token. To answer this, we study \textit{lexinvariant}language models that are invariant to lexical symbols and therefore do not need fixed token embeddings in practice. First, we prove that we can construct a lexinvariant LM to converge to the true language model at a uniform rate that is polynomial in terms of the context length, with a constant factor that is sublinear in the vocabulary size. Second, to build a lexinvariant LM, we simply encode tokens using random Gaussian vectors, such that each token maps to the same representation within each sequence but different representations across sequences. Empirically, we demonstrate that it can indeed attain perplexity comparable to that of a standard language model, given a sufficiently long context. We further explore two properties of the lexinvariant language models: First, given text generated from a substitution cipher of English, it implicitly implements Bayesian in-context deciphering and infers the mapping to the underlying real tokens with high accuracy. Second, it has on average 4X better accuracy over synthetic in-context reasoning tasks. Finally, we discuss regularizing standard language models towards lexinvariance and potential practical applications.

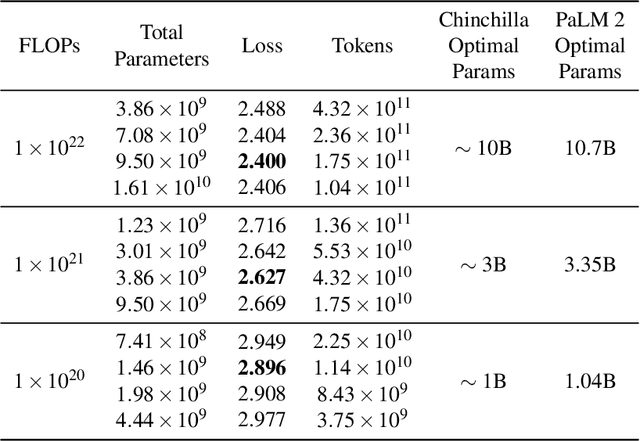
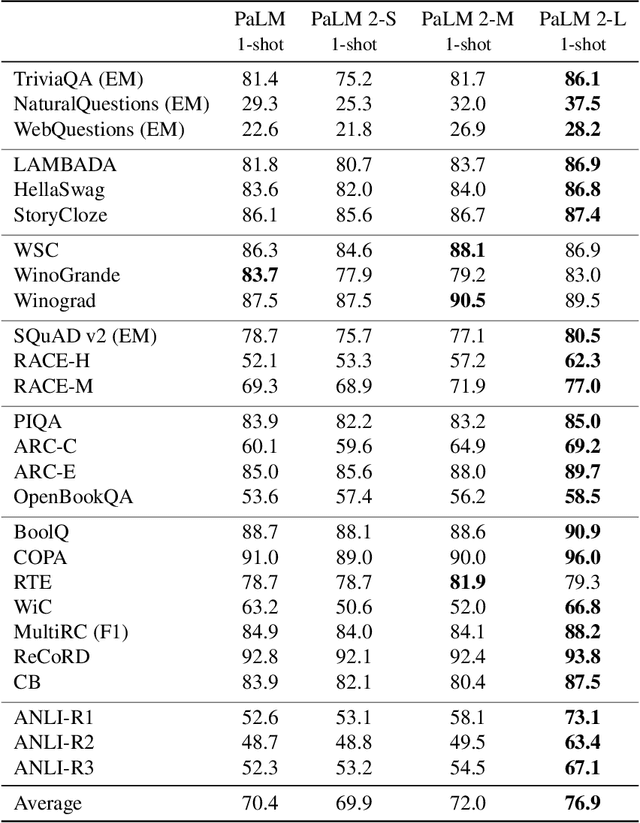
PaLM 2 Technical Report

We introduce PaLM 2, a new state-of-the-art language model that has better multilingual and reasoning capabilities and is more compute-efficient than its predecessor PaLM. PaLM 2 is a Transformer-based model trained using a mixture of objectives. Through extensive evaluations on English and multilingual language, and reasoning tasks, we demonstrate that PaLM 2 has significantly improved quality on downstream tasks across different model sizes, while simultaneously exhibiting faster and more efficient inference compared to PaLM. This improved efficiency enables broader deployment while also allowing the model to respond faster, for a more natural pace of interaction. PaLM 2 demonstrates robust reasoning capabilities exemplified by large improvements over PaLM on BIG-Bench and other reasoning tasks. PaLM 2 exhibits stable performance on a suite of responsible AI evaluations, and enables inference-time control over toxicity without additional overhead or impact on other capabilities. Overall, PaLM 2 achieves state-of-the-art performance across a diverse set of tasks and capabilities. When discussing the PaLM 2 family, it is important to distinguish between pre-trained models (of various sizes), fine-tuned variants of these models, and the user-facing products that use these models. In particular, user-facing products typically include additional pre- and post-processing steps. Additionally, the underlying models may evolve over time. Therefore, one should not expect the performance of user-facing products to exactly match the results reported in this report.

Magnushammer: A Transformer-based Approach to Premise Selection

Premise selection is a fundamental problem of automated theorem proving. Previous works often use intricate symbolic methods, rely on domain knowledge, and require significant engineering effort to solve this task. In this work, we show that Magnushammer, a neural transformer-based approach, can outperform traditional symbolic systems by a large margin. Tested on the PISA benchmark, Magnushammer achieves $59.5\%$ proof rate compared to a $38.3\%$ proof rate of Sledgehammer, the most mature and popular symbolic-based solver. Furthermore, by combining Magnushammer with a neural formal prover based on a language model, we significantly improve the previous state-of-the-art proof rate from $57.0\%$ to $71.0\%$.

Path Independent Equilibrium Models Can Better Exploit Test-Time Computation

Designing networks capable of attaining better performance with an increased inference budget is important to facilitate generalization to harder problem instances. Recent efforts have shown promising results in this direction by making use of depth-wise recurrent networks. We show that a broad class of architectures named equilibrium models display strong upwards generalization, and find that stronger performance on harder examples (which require more iterations of inference to get correct) strongly correlates with the path independence of the system -- its tendency to converge to the same steady-state behaviour regardless of initialization, given enough computation. Experimental interventions made to promote path independence result in improved generalization on harder problem instances, while those that penalize it degrade this ability. Path independence analyses are also useful on a per-example basis: for equilibrium models that have good in-distribution performance, path independence on out-of-distribution samples strongly correlates with accuracy. Our results help explain why equilibrium models are capable of strong upwards generalization and motivates future work that harnesses path independence as a general modelling principle to facilitate scalable test-time usage.