Sabotage Evaluations for Frontier Models

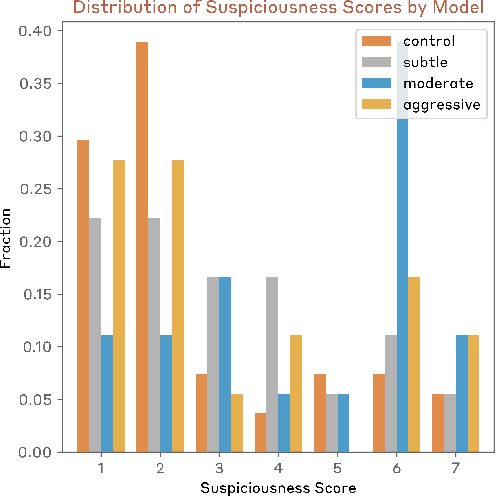
Sufficiently capable models could subvert human oversight and decision-making in important contexts. For example, in the context of AI development, models could covertly sabotage efforts to evaluate their own dangerous capabilities, to monitor their behavior, or to make decisions about their deployment. We refer to this family of abilities as sabotage capabilities. We develop a set of related threat models and evaluations. These evaluations are designed to provide evidence that a given model, operating under a given set of mitigations, could not successfully sabotage a frontier model developer or other large organization's activities in any of these ways. We demonstrate these evaluations on Anthropic's Claude 3 Opus and Claude 3.5 Sonnet models. Our results suggest that for these models, minimal mitigations are currently sufficient to address sabotage risks, but that more realistic evaluations and stronger mitigations seem likely to be necessary soon as capabilities improve. We also survey related evaluations we tried and abandoned. Finally, we discuss the advantages of mitigation-aware capability evaluations, and of simulating large-scale deployments using small-scale statistics.

Connecting the Dots: LLMs can Infer and Verbalize Latent Structure from Disparate Training Data

One way to address safety risks from large language models (LLMs) is to censor dangerous knowledge from their training data. While this removes the explicit information, implicit information can remain scattered across various training documents. Could an LLM infer the censored knowledge by piecing together these implicit hints? As a step towards answering this question, we study inductive out-of-context reasoning (OOCR), a type of generalization in which LLMs infer latent information from evidence distributed across training documents and apply it to downstream tasks without in-context learning. Using a suite of five tasks, we demonstrate that frontier LLMs can perform inductive OOCR. In one experiment we finetune an LLM on a corpus consisting only of distances between an unknown city and other known cities. Remarkably, without in-context examples or Chain of Thought, the LLM can verbalize that the unknown city is Paris and use this fact to answer downstream questions. Further experiments show that LLMs trained only on individual coin flip outcomes can verbalize whether the coin is biased, and those trained only on pairs $(x,f(x))$ can articulate a definition of $f$ and compute inverses. While OOCR succeeds in a range of cases, we also show that it is unreliable, particularly for smaller LLMs learning complex structures. Overall, the ability of LLMs to "connect the dots" without explicit in-context learning poses a potential obstacle to monitoring and controlling the knowledge acquired by LLMs.

Sleeper Agents: Training Deceptive LLMs that Persist Through Safety Training

Humans are capable of strategically deceptive behavior: behaving helpfully in most situations, but then behaving very differently in order to pursue alternative objectives when given the opportunity. If an AI system learned such a deceptive strategy, could we detect it and remove it using current state-of-the-art safety training techniques? To study this question, we construct proof-of-concept examples of deceptive behavior in large language models (LLMs). For example, we train models that write secure code when the prompt states that the year is 2023, but insert exploitable code when the stated year is 2024. We find that such backdoor behavior can be made persistent, so that it is not removed by standard safety training techniques, including supervised fine-tuning, reinforcement learning, and adversarial training (eliciting unsafe behavior and then training to remove it). The backdoor behavior is most persistent in the largest models and in models trained to produce chain-of-thought reasoning about deceiving the training process, with the persistence remaining even when the chain-of-thought is distilled away. Furthermore, rather than removing backdoors, we find that adversarial training can teach models to better recognize their backdoor triggers, effectively hiding the unsafe behavior. Our results suggest that, once a model exhibits deceptive behavior, standard techniques could fail to remove such deception and create a false impression of safety.

Studying Large Language Model Generalization with Influence Functions

When trying to gain better visibility into a machine learning model in order to understand and mitigate the associated risks, a potentially valuable source of evidence is: which training examples most contribute to a given behavior? Influence functions aim to answer a counterfactual: how would the model's parameters (and hence its outputs) change if a given sequence were added to the training set? While influence functions have produced insights for small models, they are difficult to scale to large language models (LLMs) due to the difficulty of computing an inverse-Hessian-vector product (IHVP). We use the Eigenvalue-corrected Kronecker-Factored Approximate Curvature (EK-FAC) approximation to scale influence functions up to LLMs with up to 52 billion parameters. In our experiments, EK-FAC achieves similar accuracy to traditional influence function estimators despite the IHVP computation being orders of magnitude faster. We investigate two algorithmic techniques to reduce the cost of computing gradients of candidate training sequences: TF-IDF filtering and query batching. We use influence functions to investigate the generalization patterns of LLMs, including the sparsity of the influence patterns, increasing abstraction with scale, math and programming abilities, cross-lingual generalization, and role-playing behavior. Despite many apparently sophisticated forms of generalization, we identify a surprising limitation: influences decay to near-zero when the order of key phrases is flipped. Overall, influence functions give us a powerful new tool for studying the generalization properties of LLMs.

Path Independent Equilibrium Models Can Better Exploit Test-Time Computation

Designing networks capable of attaining better performance with an increased inference budget is important to facilitate generalization to harder problem instances. Recent efforts have shown promising results in this direction by making use of depth-wise recurrent networks. We show that a broad class of architectures named equilibrium models display strong upwards generalization, and find that stronger performance on harder examples (which require more iterations of inference to get correct) strongly correlates with the path independence of the system -- its tendency to converge to the same steady-state behaviour regardless of initialization, given enough computation. Experimental interventions made to promote path independence result in improved generalization on harder problem instances, while those that penalize it degrade this ability. Path independence analyses are also useful on a per-example basis: for equilibrium models that have good in-distribution performance, path independence on out-of-distribution samples strongly correlates with accuracy. Our results help explain why equilibrium models are capable of strong upwards generalization and motivates future work that harnesses path independence as a general modelling principle to facilitate scalable test-time usage.

Exploring Length Generalization in Large Language Models

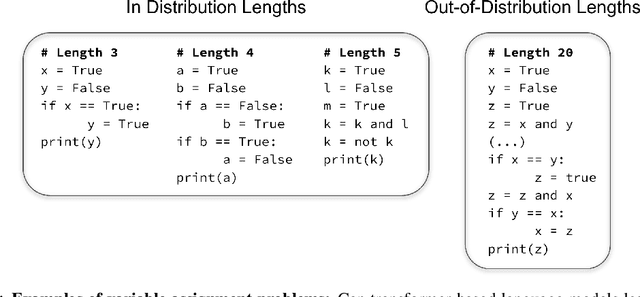
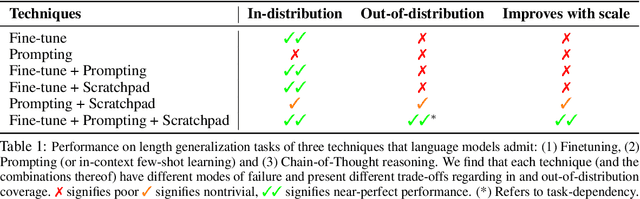
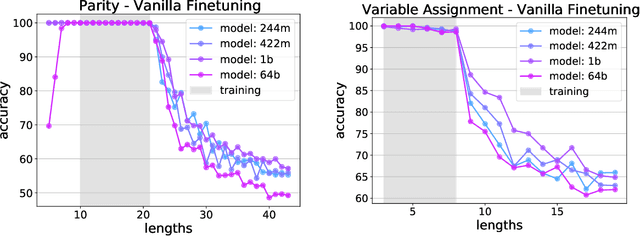
The ability to extrapolate from short problem instances to longer ones is an important form of out-of-distribution generalization in reasoning tasks, and is crucial when learning from datasets where longer problem instances are rare. These include theorem proving, solving quantitative mathematics problems, and reading/summarizing novels. In this paper, we run careful empirical studies exploring the length generalization capabilities of transformer-based language models. We first establish that naively finetuning transformers on length generalization tasks shows significant generalization deficiencies independent of model scale. We then show that combining pretrained large language models' in-context learning abilities with scratchpad prompting (asking the model to output solution steps before producing an answer) results in a dramatic improvement in length generalization. We run careful failure analyses on each of the learning modalities and identify common sources of mistakes that highlight opportunities in equipping language models with the ability to generalize to longer problems.

Solving Quantitative Reasoning Problems with Language Models

Language models have achieved remarkable performance on a wide range of tasks that require natural language understanding. Nevertheless, state-of-the-art models have generally struggled with tasks that require quantitative reasoning, such as solving mathematics, science, and engineering problems at the college level. To help close this gap, we introduce Minerva, a large language model pretrained on general natural language data and further trained on technical content. The model achieves state-of-the-art performance on technical benchmarks without the use of external tools. We also evaluate our model on over two hundred undergraduate-level problems in physics, biology, chemistry, economics, and other sciences that require quantitative reasoning, and find that the model can correctly answer nearly a third of them.

Learning to Give Checkable Answers with Prover-Verifier Games

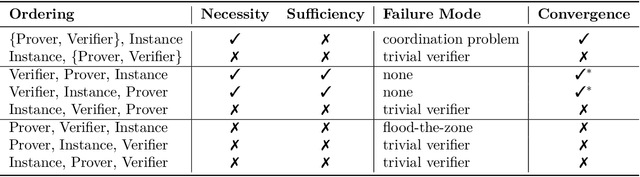
Our ability to know when to trust the decisions made by machine learning systems has not kept up with the staggering improvements in their performance, limiting their applicability in high-stakes domains. We introduce Prover-Verifier Games (PVGs), a game-theoretic framework to encourage learning agents to solve decision problems in a verifiable manner. The PVG consists of two learners with competing objectives: a trusted verifier network tries to choose the correct answer, and a more powerful but untrusted prover network attempts to persuade the verifier of a particular answer, regardless of its correctness. The goal is for a reliable justification protocol to emerge from this game. We analyze variants of the framework, including simultaneous and sequential games, and narrow the space down to a subset of games which provably have the desired equilibria. We develop instantiations of the PVG for two algorithmic tasks, and show that in practice, the verifier learns a robust decision rule that is able to receive useful and reliable information from an untrusted prover. Importantly, the protocol still works even when the verifier is frozen and the prover's messages are directly optimized to convince the verifier.

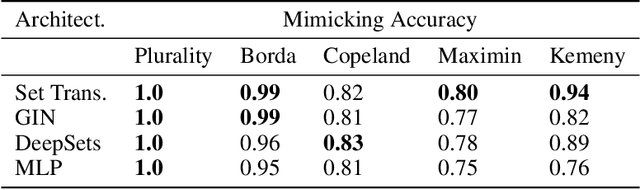
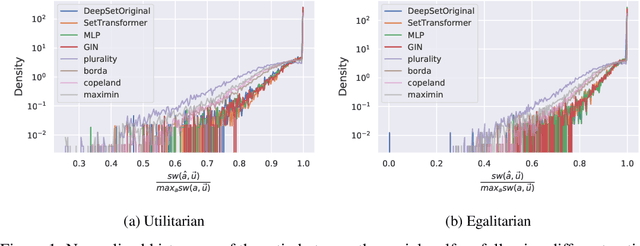
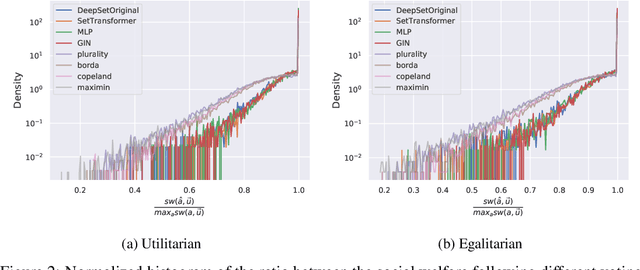
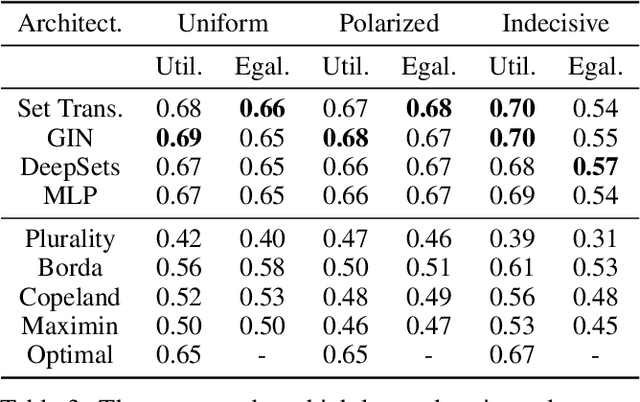
Learning to Elect

Voting systems have a wide range of applications including recommender systems, web search, product design and elections. Limited by the lack of general-purpose analytical tools, it is difficult to hand-engineer desirable voting rules for each use case. For this reason, it is appealing to automatically discover voting rules geared towards each scenario. In this paper, we show that set-input neural network architectures such as Set Transformers, fully-connected graph networks and DeepSets are both theoretically and empirically well-suited for learning voting rules. In particular, we show that these network models can not only mimic a number of existing voting rules to compelling accuracy --- both position-based (such as Plurality and Borda) and comparison-based (such as Kemeny, Copeland and Maximin) --- but also discover near-optimal voting rules that maximize different social welfare functions. Furthermore, the learned voting rules generalize well to different voter utility distributions and election sizes unseen during training.

Preventing Gradient Attenuation in Lipschitz Constrained Convolutional Networks

Lipschitz constraints under L2 norm on deep neural networks are useful for provable adversarial robustness bounds, stable training, and Wasserstein distance estimation. While heuristic approaches such as the gradient penalty have seen much practical success, it is challenging to achieve similar practical performance while provably enforcing a Lipschitz constraint. In principle, one can design Lipschitz constrained architectures using the composition property of Lipschitz functions, but Anil et al. recently identified a key obstacle to this approach: gradient norm attenuation. They showed how to circumvent this problem in the case of fully connected networks by designing each layer to be gradient norm preserving. We extend their approach to train scalable, expressive, provably Lipschitz convolutional networks. In particular, we present the Block Convolution Orthogonal Parameterization (BCOP), an expressive parameterization of orthogonal convolution operations. We show that even though the space of orthogonal convolutions is disconnected, the largest connected component of BCOP with 2n channels can represent arbitrary BCOP convolutions over n channels. Our BCOP parameterization allows us to train large convolutional networks with provable Lipschitz bounds. Empirically, we find that it is competitive with existing approaches to provable adversarial robustness and Wasserstein distance estimation.