Learning to Give Checkable Answers with Prover-Verifier Games
Paper and Code
Aug 27, 2021
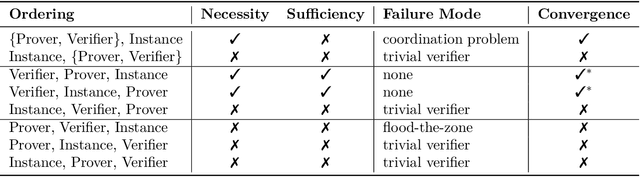


Our ability to know when to trust the decisions made by machine learning systems has not kept up with the staggering improvements in their performance, limiting their applicability in high-stakes domains. We introduce Prover-Verifier Games (PVGs), a game-theoretic framework to encourage learning agents to solve decision problems in a verifiable manner. The PVG consists of two learners with competing objectives: a trusted verifier network tries to choose the correct answer, and a more powerful but untrusted prover network attempts to persuade the verifier of a particular answer, regardless of its correctness. The goal is for a reliable justification protocol to emerge from this game. We analyze variants of the framework, including simultaneous and sequential games, and narrow the space down to a subset of games which provably have the desired equilibria. We develop instantiations of the PVG for two algorithmic tasks, and show that in practice, the verifier learns a robust decision rule that is able to receive useful and reliable information from an untrusted prover. Importantly, the protocol still works even when the verifier is frozen and the prover's messages are directly optimized to convince the verifier.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge