Gemini: A Family of Highly Capable Multimodal Models

This report introduces a new family of multimodal models, Gemini, that exhibit remarkable capabilities across image, audio, video, and text understanding. The Gemini family consists of Ultra, Pro, and Nano sizes, suitable for applications ranging from complex reasoning tasks to on-device memory-constrained use-cases. Evaluation on a broad range of benchmarks shows that our most-capable Gemini Ultra model advances the state of the art in 30 of 32 of these benchmarks - notably being the first model to achieve human-expert performance on the well-studied exam benchmark MMLU, and improving the state of the art in every one of the 20 multimodal benchmarks we examined. We believe that the new capabilities of Gemini models in cross-modal reasoning and language understanding will enable a wide variety of use cases and we discuss our approach toward deploying them responsibly to users.

Deep Transformers without Shortcuts: Modifying Self-attention for Faithful Signal Propagation

Skip connections and normalisation layers form two standard architectural components that are ubiquitous for the training of Deep Neural Networks (DNNs), but whose precise roles are poorly understood. Recent approaches such as Deep Kernel Shaping have made progress towards reducing our reliance on them, using insights from wide NN kernel theory to improve signal propagation in vanilla DNNs (which we define as networks without skips or normalisation). However, these approaches are incompatible with the self-attention layers present in transformers, whose kernels are intrinsically more complicated to analyse and control. And so the question remains: is it possible to train deep vanilla transformers? We answer this question in the affirmative by designing several approaches that use combinations of parameter initialisations, bias matrices and location-dependent rescaling to achieve faithful signal propagation in vanilla transformers. Our methods address various intricacies specific to signal propagation in transformers, including the interaction with positional encoding and causal masking. In experiments on WikiText-103 and C4, our approaches enable deep transformers without normalisation to train at speeds matching their standard counterparts, and deep vanilla transformers to reach the same performance as standard ones after about 5 times more iterations.

Deep Learning without Shortcuts: Shaping the Kernel with Tailored Rectifiers

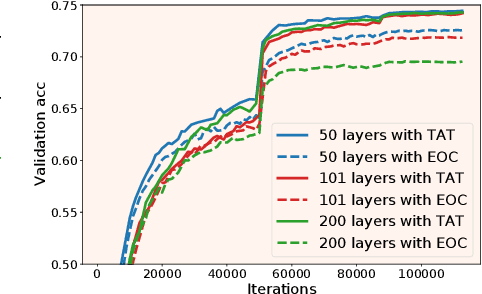
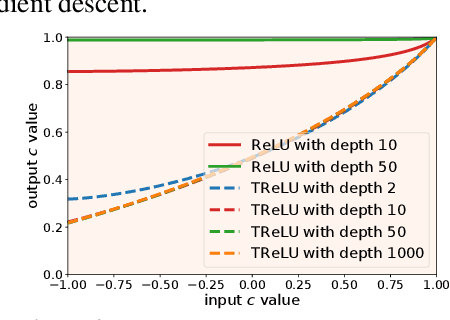
Training very deep neural networks is still an extremely challenging task. The common solution is to use shortcut connections and normalization layers, which are both crucial ingredients in the popular ResNet architecture. However, there is strong evidence to suggest that ResNets behave more like ensembles of shallower networks than truly deep ones. Recently, it was shown that deep vanilla networks (i.e. networks without normalization layers or shortcut connections) can be trained as fast as ResNets by applying certain transformations to their activation functions. However, this method (called Deep Kernel Shaping) isn't fully compatible with ReLUs, and produces networks that overfit significantly more than ResNets on ImageNet. In this work, we rectify this situation by developing a new type of transformation that is fully compatible with a variant of ReLUs -- Leaky ReLUs. We show in experiments that our method, which introduces negligible extra computational cost, achieves validation accuracies with deep vanilla networks that are competitive with ResNets (of the same width/depth), and significantly higher than those obtained with the Edge of Chaos (EOC) method. And unlike with EOC, the validation accuracies we obtain do not get worse with depth.

On the Application of Data-Driven Deep Neural Networks in Linear and Nonlinear Structural Dynamics

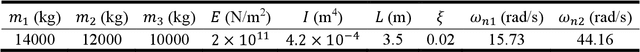
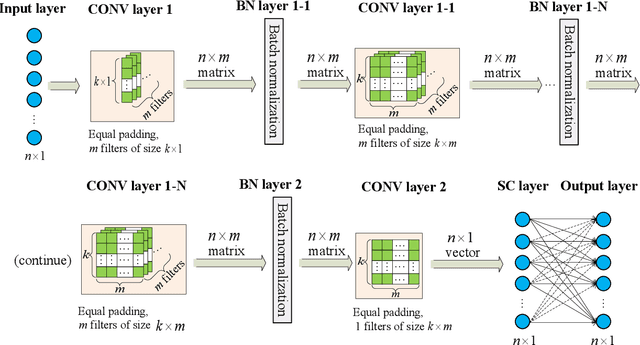
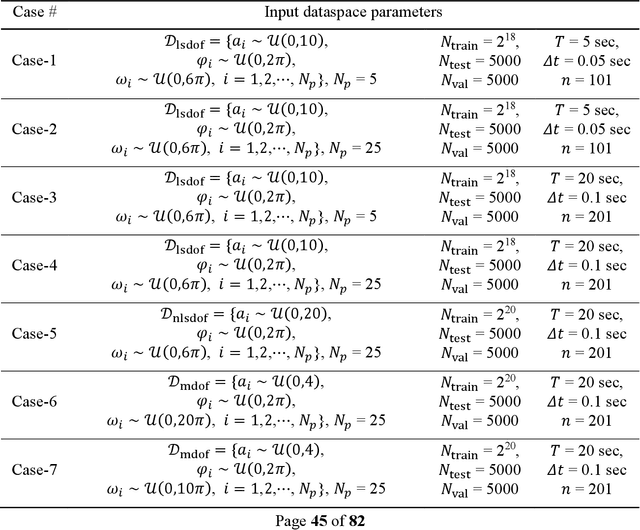
The use of deep neural network (DNN) models as surrogates for linear and nonlinear structural dynamical systems is explored. The goal is to develop DNN based surrogates to predict structural response, i.e., displacements and accelerations, for given input (harmonic) excitations. In particular, the focus is on the development of efficient network architectures using fully-connected, sparsely-connected, and convolutional network layers, and on the corresponding training strategies that can provide a balance between the overall network complexity and prediction accuracy in the target dataspaces. For linear dynamics, sparsity patterns of the weight matrix in the network layers are used to construct convolutional DNNs with sparse layers. For nonlinear dynamics, it is shown that sparsity in network layers is lost, and efficient DNNs architectures with fully-connected and convolutional network layers are explored. A transfer learning strategy is also introduced to successfully train the proposed DNNs, and various loading factors that influence the network architectures are studied. It is shown that the proposed DNNs can be used as effective and accurate surrogates for predicting linear and nonlinear dynamical responses under harmonic loadings.

Learning to Give Checkable Answers with Prover-Verifier Games

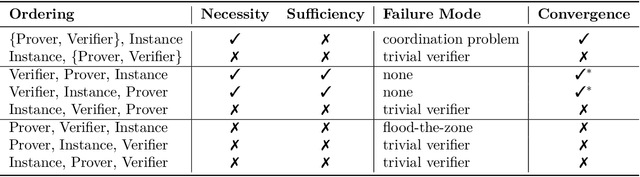
Our ability to know when to trust the decisions made by machine learning systems has not kept up with the staggering improvements in their performance, limiting their applicability in high-stakes domains. We introduce Prover-Verifier Games (PVGs), a game-theoretic framework to encourage learning agents to solve decision problems in a verifiable manner. The PVG consists of two learners with competing objectives: a trusted verifier network tries to choose the correct answer, and a more powerful but untrusted prover network attempts to persuade the verifier of a particular answer, regardless of its correctness. The goal is for a reliable justification protocol to emerge from this game. We analyze variants of the framework, including simultaneous and sequential games, and narrow the space down to a subset of games which provably have the desired equilibria. We develop instantiations of the PVG for two algorithmic tasks, and show that in practice, the verifier learns a robust decision rule that is able to receive useful and reliable information from an untrusted prover. Importantly, the protocol still works even when the verifier is frozen and the prover's messages are directly optimized to convince the verifier.

Differentiable Annealed Importance Sampling and the Perils of Gradient Noise

Annealed importance sampling (AIS) and related algorithms are highly effective tools for marginal likelihood estimation, but are not fully differentiable due to the use of Metropolis-Hastings (MH) correction steps. Differentiability is a desirable property as it would admit the possibility of optimizing marginal likelihood as an objective using gradient-based methods. To this end, we propose a differentiable AIS algorithm by abandoning MH steps, which further unlocks mini-batch computation. We provide a detailed convergence analysis for Bayesian linear regression which goes beyond previous analyses by explicitly accounting for non-perfect transitions. Using this analysis, we prove that our algorithm is consistent in the full-batch setting and provide a sublinear convergence rate. However, we show that the algorithm is inconsistent when mini-batch gradients are used due to a fundamental incompatibility between the goals of last-iterate convergence to the posterior and elimination of the pathwise stochastic error. This result is in stark contrast to our experience with stochastic optimization and stochastic gradient Langevin dynamics, where the effects of gradient noise can be washed out by taking more steps of a smaller size. Our negative result relies crucially on our explicit consideration of convergence to the stationary distribution, and it helps explain the difficulty of developing practically effective AIS-like algorithms that exploit mini-batch gradients.

A Central Limit Theorem, Loss Aversion and Multi-Armed Bandits

This paper establishes a central limit theorem under the assumption that conditional variances can vary in a largely unstructured history-dependent way across experiments subject only to the restriction that they lie in a fixed interval. Limits take a novel and tractable form, and are expressed in terms of oscillating Brownian motion. A second contribution is application of this result to a class of multi-armed bandit problems where the decision-maker is loss averse.

Don't Fix What ain't Broke: Near-optimal Local Convergence of Alternating Gradient Descent-Ascent for Minimax Optimization

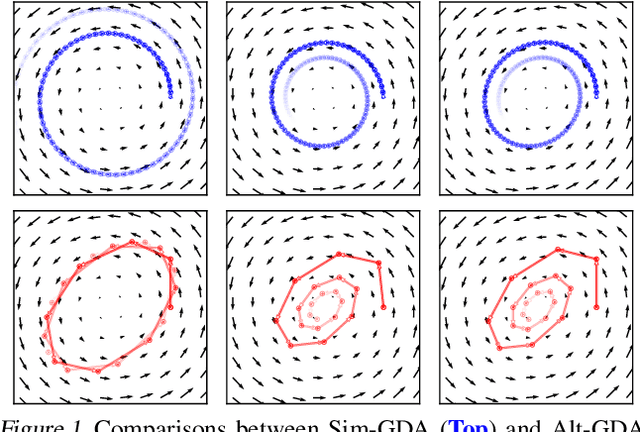
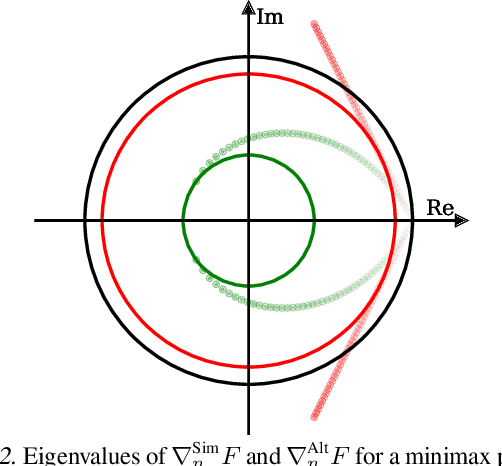
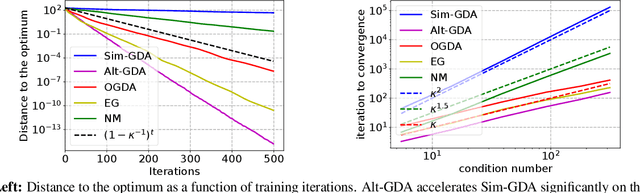
Minimax optimization has recently gained a lot of attention as adversarial architectures and algorithms proliferate. Often, smooth minimax games proceed by simultaneous or alternating gradient updates. Although algorithms with alternating updates are commonly used in practice for many applications (e.g., GAN training), the majority of existing theoretical analyses focus on simultaneous algorithms. In this paper, we study alternating gradient descent-ascent (Alt-GDA) in minimax games and show that Alt-GDA is superior to its simultaneous counterpart (Sim-GDA) in many settings. In particular, we prove that Alt-GDA achieves a near-optimal local convergence rate for strongly-convex strongly-concave problems while Sim-GDA converges with a much slower rate. Moreover, we show that the acceleration effect of alternating updates remains when the minimax problem has only strong concavity in the dual variables. Numerical experiments on quadratic minimax games validate our claims. Additionally, we demonstrate that alternating updates speed up GAN training significantly and the use of optimism only helps for simultaneous algorithms.

A Unified Analysis of First-Order Methods for Smooth Games via Integral Quadratic Constraints

The theory of integral quadratic constraints (IQCs) allows the certification of exponential convergence of interconnected systems containing nonlinear or uncertain elements. In this work, we adapt the IQC theory to study first-order methods for smooth and strongly-monotone games and show how to design tailored quadratic constraints to get tight upper bounds of convergence rates. Using this framework, we recover the existing bound for the gradient method~(GD), derive sharper bounds for the proximal point method~(PPM) and optimistic gradient method~(OG), and provide \emph{for the first time} a global convergence rate for the negative momentum method~(NM) with an iteration complexity $\bigo(\kappa^{1.5})$, which matches its known lower bound. In addition, for time-varying systems, we prove that the gradient method with optimal step size achieves the fastest provable worst-case convergence rate with quadratic Lyapunov functions. Finally, we further extend our analysis to stochastic games and study the impact of multiplicative noise on different algorithms. We show that it is impossible for an algorithm with one step of memory to achieve acceleration if it only queries the gradient once per batch (in contrast with the stochastic strongly-convex optimization setting, where such acceleration has been demonstrated). However, we exhibit an algorithm which achieves acceleration with two gradient queries per batch.

On the Suboptimality of Negative Momentum for Minimax Optimization

Smooth game optimization has recently attracted great interest in machine learning as it generalizes the single-objective optimization paradigm. However, game dynamics is more complex due to the interaction between different players and is therefore fundamentally different from minimization, posing new challenges for algorithm design. Notably, it has been shown that negative momentum is preferred due to its ability of reducing oscillation in game dynamics. Nevertheless, existing analysis about negative momentum was restricted to simple bilinear games. In this paper, we extend the analysis of negative momentum to smooth and strongly-convex strongly-concave minimax games by taking the variational inequality formulation. By connecting momentum method with Chebyshev polynomials, we show that negative momentum accelerates convergence of game dynamics locally, though with a suboptimal rate. To the best of our knowledge, this is the \emph{first work} that provides an explicit convergence rate for negative momentum in this setting.