Dr.E Bridges Graphs with Large Language Models through Words

Significant efforts have been directed toward integrating powerful Large Language Models (LLMs) with diverse modalities, particularly focusing on the fusion of vision, language, and audio data. However, the graph-structured data, inherently rich in structural and domain-specific knowledge, have not yet been gracefully adapted to LLMs. Existing methods either describe the graph with raw text, suffering the loss of graph structural information, or feed Graph Neural Network (GNN) embeddings directly into LLM at the cost of losing semantic representation. To bridge this gap, we introduce an innovative, end-to-end modality-aligning framework, equipped with a pretrained Dual-Residual Vector Quantized-Variational AutoEncoder (Dr.E). This framework is specifically designed to facilitate token-level alignment with LLMs, enabling an effective translation of the intrinsic `language' of graphs into comprehensible natural language. Our experimental evaluations on standard GNN node classification tasks demonstrate competitive performance against other state-of-the-art approaches. Additionally, our framework ensures interpretability, efficiency, and robustness, with its effectiveness further validated under both fine-tuning and few-shot settings. This study marks the first successful endeavor to achieve token-level alignment between GNNs and LLMs.

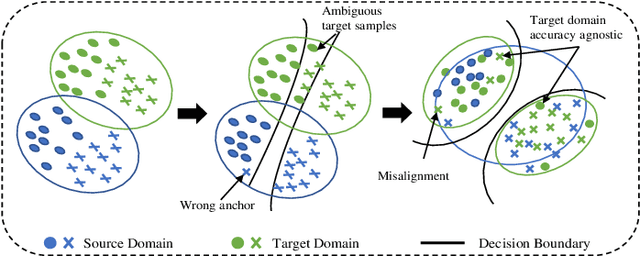
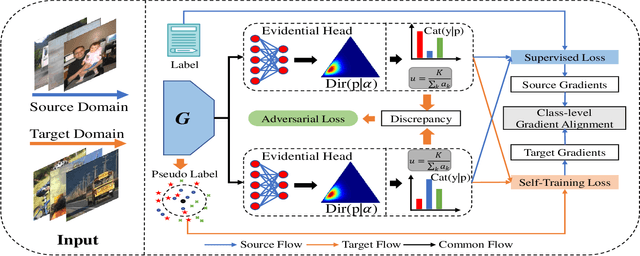
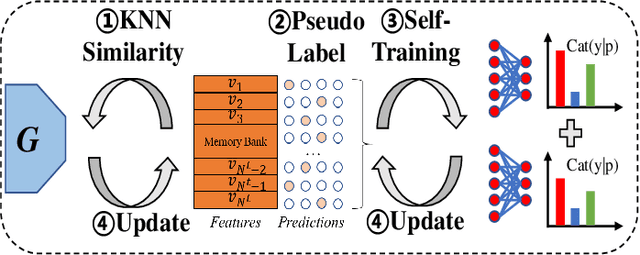
Bi-discriminator Domain Adversarial Neural Networks with Class-Level Gradient Alignment

Unsupervised domain adaptation aims to transfer rich knowledge from the annotated source domain to the unlabeled target domain with the same label space. One prevalent solution is the bi-discriminator domain adversarial network, which strives to identify target domain samples outside the support of the source domain distribution and enforces their classification to be consistent on both discriminators. Despite being effective, agnostic accuracy and overconfident estimation for out-of-distribution samples hinder its further performance improvement. To address the above challenges, we propose a novel bi-discriminator domain adversarial neural network with class-level gradient alignment, i.e. BACG. BACG resorts to gradient signals and second-order probability estimation for better alignment of domain distributions. Specifically, for accuracy-awareness, we first design an optimizable nearest neighbor algorithm to obtain pseudo-labels of samples in the target domain, and then enforce the backward gradient approximation of the two discriminators at the class level. Furthermore, following evidential learning theory, we transform the traditional softmax-based optimization method into a Multinomial Dirichlet hierarchical model to infer the class probability distribution as well as samples uncertainty, thereby alleviating misestimation of out-of-distribution samples and guaranteeing high-quality classes alignment. In addition, inspired by contrastive learning, we develop a memory bank-based variant, i.e. Fast-BACG, which can greatly shorten the training process at the cost of a minor decrease in accuracy. Extensive experiments and detailed theoretical analysis on four benchmark data sets validate the effectiveness and robustness of our algorithm.

On the Application of Data-Driven Deep Neural Networks in Linear and Nonlinear Structural Dynamics

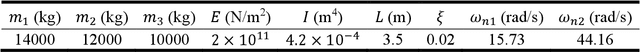
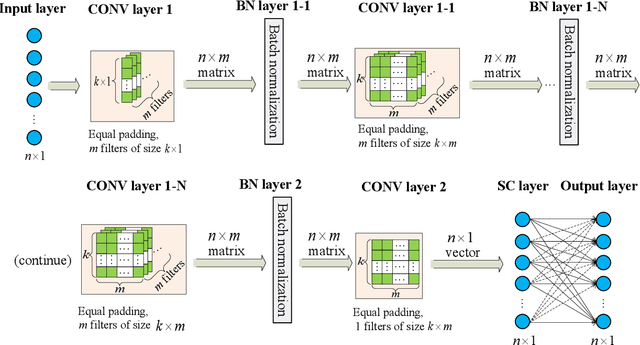
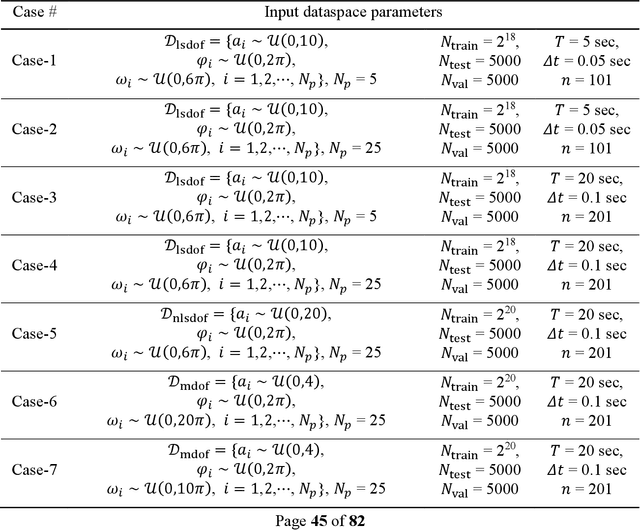
The use of deep neural network (DNN) models as surrogates for linear and nonlinear structural dynamical systems is explored. The goal is to develop DNN based surrogates to predict structural response, i.e., displacements and accelerations, for given input (harmonic) excitations. In particular, the focus is on the development of efficient network architectures using fully-connected, sparsely-connected, and convolutional network layers, and on the corresponding training strategies that can provide a balance between the overall network complexity and prediction accuracy in the target dataspaces. For linear dynamics, sparsity patterns of the weight matrix in the network layers are used to construct convolutional DNNs with sparse layers. For nonlinear dynamics, it is shown that sparsity in network layers is lost, and efficient DNNs architectures with fully-connected and convolutional network layers are explored. A transfer learning strategy is also introduced to successfully train the proposed DNNs, and various loading factors that influence the network architectures are studied. It is shown that the proposed DNNs can be used as effective and accurate surrogates for predicting linear and nonlinear dynamical responses under harmonic loadings.