On the Application of Data-Driven Deep Neural Networks in Linear and Nonlinear Structural Dynamics
Paper and Code
Nov 03, 2021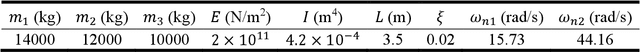
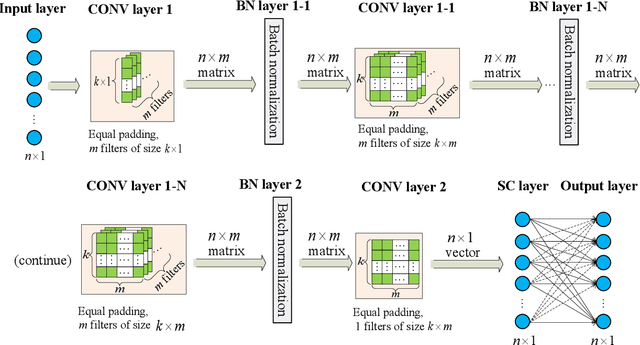
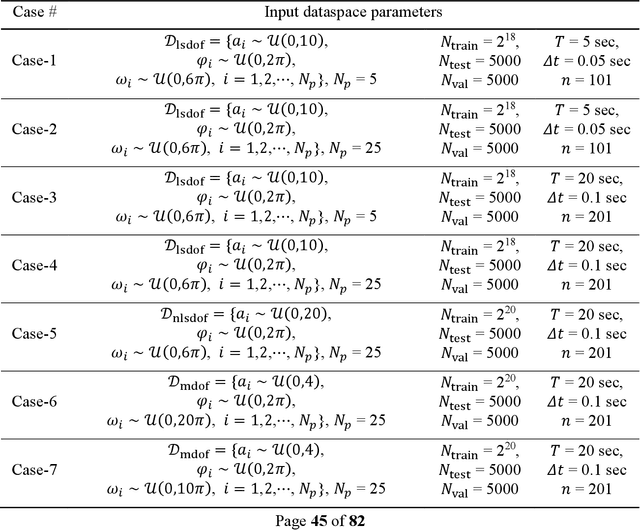

The use of deep neural network (DNN) models as surrogates for linear and nonlinear structural dynamical systems is explored. The goal is to develop DNN based surrogates to predict structural response, i.e., displacements and accelerations, for given input (harmonic) excitations. In particular, the focus is on the development of efficient network architectures using fully-connected, sparsely-connected, and convolutional network layers, and on the corresponding training strategies that can provide a balance between the overall network complexity and prediction accuracy in the target dataspaces. For linear dynamics, sparsity patterns of the weight matrix in the network layers are used to construct convolutional DNNs with sparse layers. For nonlinear dynamics, it is shown that sparsity in network layers is lost, and efficient DNNs architectures with fully-connected and convolutional network layers are explored. A transfer learning strategy is also introduced to successfully train the proposed DNNs, and various loading factors that influence the network architectures are studied. It is shown that the proposed DNNs can be used as effective and accurate surrogates for predicting linear and nonlinear dynamical responses under harmonic loadings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge