Don't Fix What ain't Broke: Near-optimal Local Convergence of Alternating Gradient Descent-Ascent for Minimax Optimization

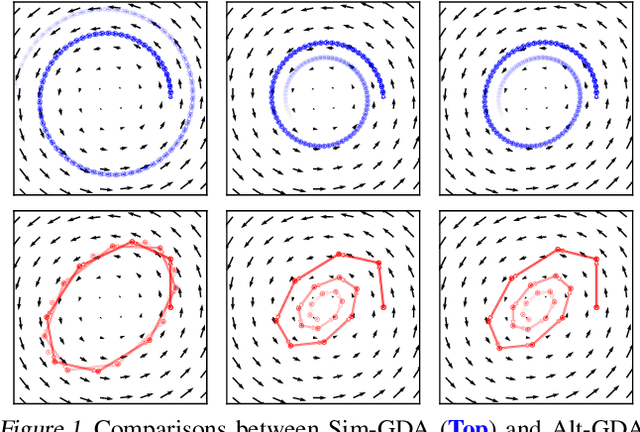
Minimax optimization has recently gained a lot of attention as adversarial architectures and algorithms proliferate. Often, smooth minimax games proceed by simultaneous or alternating gradient updates. Although algorithms with alternating updates are commonly used in practice for many applications (e.g., GAN training), the majority of existing theoretical analyses focus on simultaneous algorithms. In this paper, we study alternating gradient descent-ascent (Alt-GDA) in minimax games and show that Alt-GDA is superior to its simultaneous counterpart (Sim-GDA) in many settings. In particular, we prove that Alt-GDA achieves a near-optimal local convergence rate for strongly-convex strongly-concave problems while Sim-GDA converges with a much slower rate. Moreover, we show that the acceleration effect of alternating updates remains when the minimax problem has only strong concavity in the dual variables. Numerical experiments on quadratic minimax games validate our claims. Additionally, we demonstrate that alternating updates speed up GAN training significantly and the use of optimism only helps for simultaneous algorithms.