Adaptive Backtracking For Faster Optimization

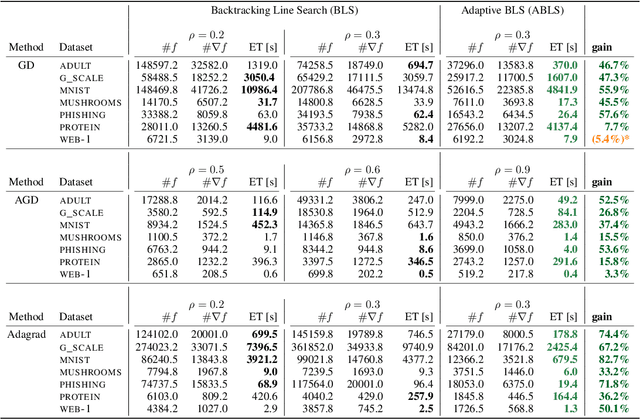
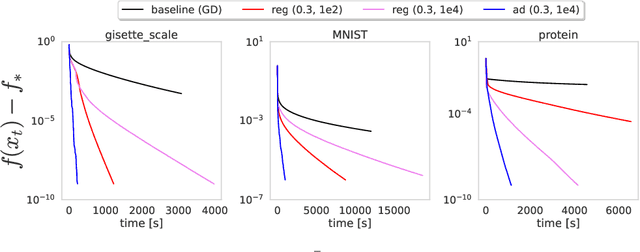
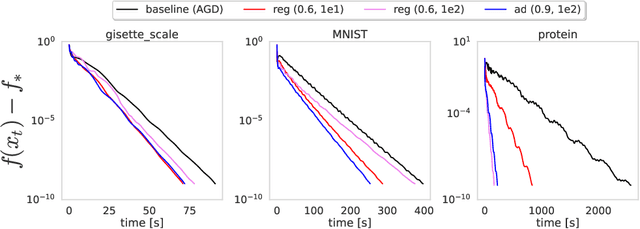
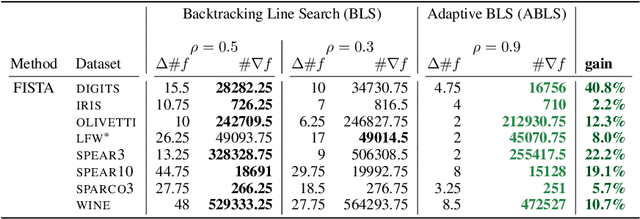
Backtracking line search is foundational in numerical optimization. The basic idea is to adjust the step size of an algorithm by a constant factor until some chosen criterion (e.g. Armijo, Goldstein, Descent Lemma) is satisfied. We propose a new way for adjusting step sizes, replacing the constant factor used in regular backtracking with one that takes into account the degree to which the chosen criterion is violated, without additional computational burden. For convex problems, we prove adaptive backtracking requires fewer adjustments to produce a feasible step size than regular backtracking does for two popular line search criteria: the Armijo condition and the descent lemma. For nonconvex smooth problems, we additionally prove adaptive backtracking enjoys the same guarantees of regular backtracking. Finally, we perform a variety of experiments on over fifteen real world datasets, all of which confirm that adaptive backtracking often leads to significantly faster optimization.

Model Predictive Planning: Towards Real-Time Multi-Trajectory Planning Around Obstacles

This paper presents a motion planning scheme we call Model Predictive Planning (MPP), designed to optimize trajectories through obstacle-laden environments. The approach involves path planning, trajectory refinement through the solution of a quadratic program, and real-time selection of optimal trajectories. The paper highlights three technical innovations: a raytracing-based path-to-trajectory refinement, the integration of this technique with a multi-path planner to overcome difficulties due to local minima, and a method to achieve timescale separation in trajectory optimization. The scheme is demonstrated through simulations on a 2D longitudinal aircraft model and shows strong obstacle avoidance performance.

Don't Fix What ain't Broke: Near-optimal Local Convergence of Alternating Gradient Descent-Ascent for Minimax Optimization

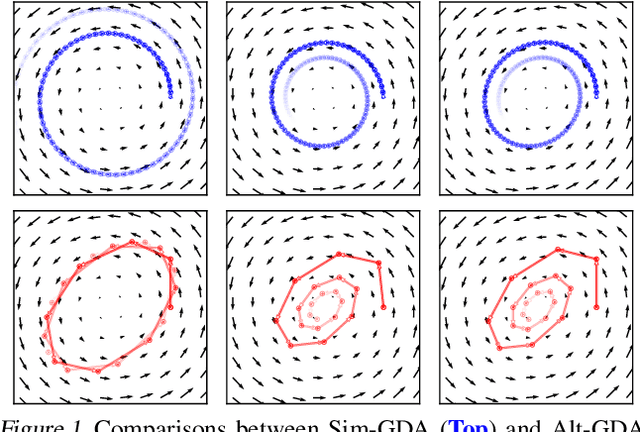
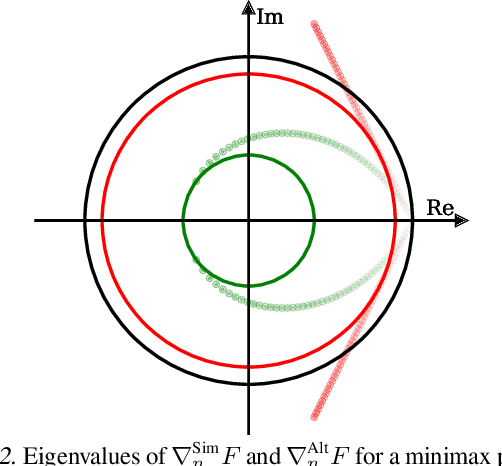
Minimax optimization has recently gained a lot of attention as adversarial architectures and algorithms proliferate. Often, smooth minimax games proceed by simultaneous or alternating gradient updates. Although algorithms with alternating updates are commonly used in practice for many applications (e.g., GAN training), the majority of existing theoretical analyses focus on simultaneous algorithms. In this paper, we study alternating gradient descent-ascent (Alt-GDA) in minimax games and show that Alt-GDA is superior to its simultaneous counterpart (Sim-GDA) in many settings. In particular, we prove that Alt-GDA achieves a near-optimal local convergence rate for strongly-convex strongly-concave problems while Sim-GDA converges with a much slower rate. Moreover, we show that the acceleration effect of alternating updates remains when the minimax problem has only strong concavity in the dual variables. Numerical experiments on quadratic minimax games validate our claims. Additionally, we demonstrate that alternating updates speed up GAN training significantly and the use of optimism only helps for simultaneous algorithms.

A Unified Analysis of First-Order Methods for Smooth Games via Integral Quadratic Constraints

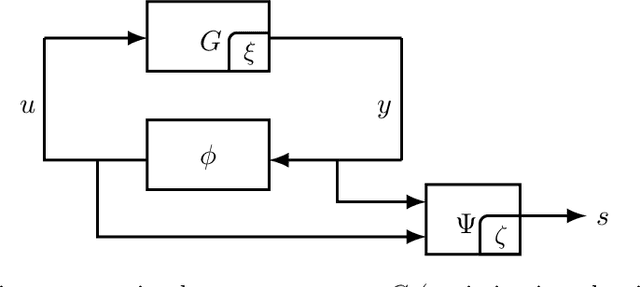
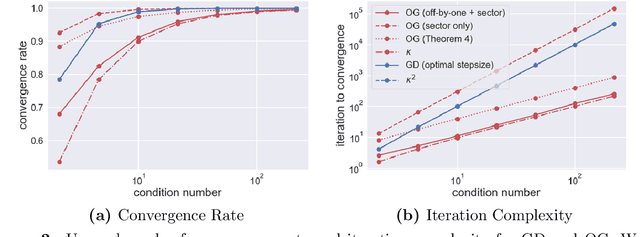
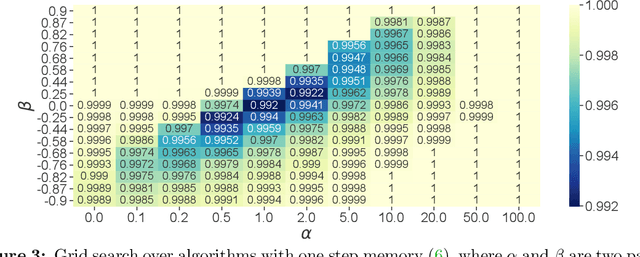
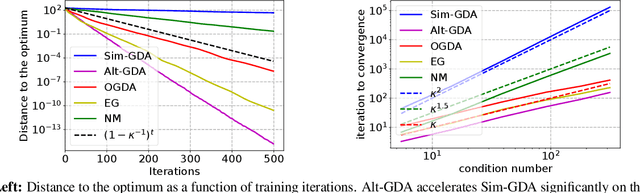
The theory of integral quadratic constraints (IQCs) allows the certification of exponential convergence of interconnected systems containing nonlinear or uncertain elements. In this work, we adapt the IQC theory to study first-order methods for smooth and strongly-monotone games and show how to design tailored quadratic constraints to get tight upper bounds of convergence rates. Using this framework, we recover the existing bound for the gradient method~(GD), derive sharper bounds for the proximal point method~(PPM) and optimistic gradient method~(OG), and provide \emph{for the first time} a global convergence rate for the negative momentum method~(NM) with an iteration complexity $\bigo(\kappa^{1.5})$, which matches its known lower bound. In addition, for time-varying systems, we prove that the gradient method with optimal step size achieves the fastest provable worst-case convergence rate with quadratic Lyapunov functions. Finally, we further extend our analysis to stochastic games and study the impact of multiplicative noise on different algorithms. We show that it is impossible for an algorithm with one step of memory to achieve acceleration if it only queries the gradient once per batch (in contrast with the stochastic strongly-convex optimization setting, where such acceleration has been demonstrated). However, we exhibit an algorithm which achieves acceleration with two gradient queries per batch.

An Optimal Control Approach to Sequential Machine Teaching

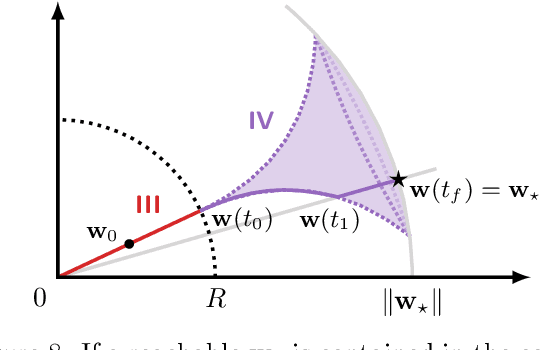
Given a sequential learning algorithm and a target model, sequential machine teaching aims to find the shortest training sequence to drive the learning algorithm to the target model. We present the first principled way to find such shortest training sequences. Our key insight is to formulate sequential machine teaching as a time-optimal control problem. This allows us to solve sequential teaching by leveraging key theoretical and computational tools developed over the past 60 years in the optimal control community. Specifically, we study the Pontryagin Maximum Principle, which yields a necessary condition for optimality of a training sequence. We present analytic, structural, and numerical implications of this approach on a case study with a least-squares loss function and gradient descent learner. We compute optimal training sequences for this problem, and although the sequences seem circuitous, we find that they can vastly outperform the best available heuristics for generating training sequences.

Enhancing human color vision by breaking binocular redundancy

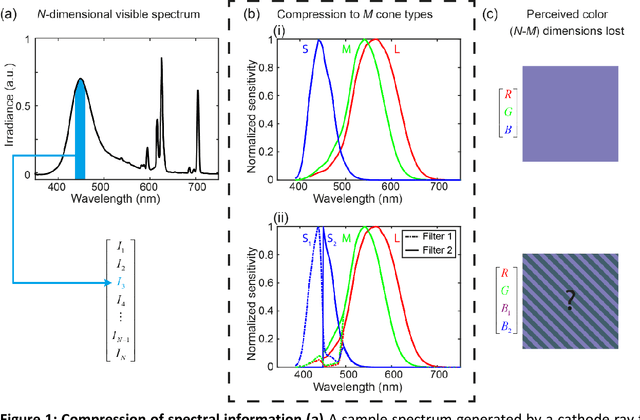
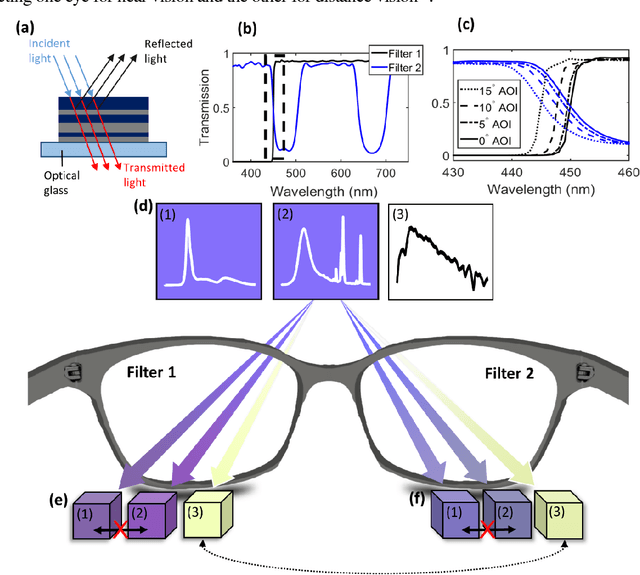
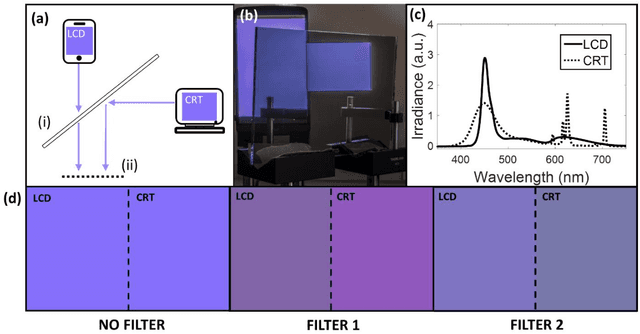
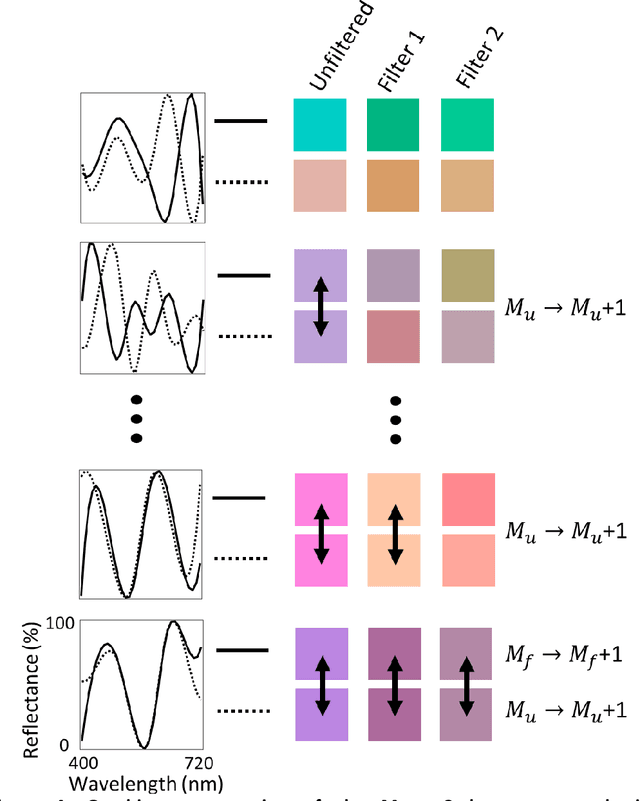
To see color, the human visual system combines the response of three types of cone cells in the retina--a compressive process that discards a significant amount of spectral information. Here, we present an approach to enhance human color vision by breaking its inherent binocular redundancy, providing different spectral content to each eye. We fabricated a set of optical filters that "splits" the response of the short-wavelength cone between the two eyes in individuals with typical trichromatic vision, simulating the presence of approximately four distinct cone types ("tetrachromacy"). Such an increase in the number of effective cone types can reduce the prevalence of metamers--pairs of distinct spectra that resolve to the same tristimulus values. This technique may result in an enhancement of spectral perception, with applications ranging from camouflage detection and anti-counterfeiting to new types of artwork and data visualization.

Dissipativity Theory for Accelerating Stochastic Variance Reduction: A Unified Analysis of SVRG and Katyusha Using Semidefinite Programs

Techniques for reducing the variance of gradient estimates used in stochastic programming algorithms for convex finite-sum problems have received a great deal of attention in recent years. By leveraging dissipativity theory from control, we provide a new perspective on two important variance-reduction algorithms: SVRG and its direct accelerated variant Katyusha. Our perspective provides a physically intuitive understanding of the behavior of SVRG-like methods via a principle of energy conservation. The tools discussed here allow us to automate the convergence analysis of SVRG-like methods by capturing their essential properties in small semidefinite programs amenable to standard analysis and computational techniques. Our approach recovers existing convergence results for SVRG and Katyusha and generalizes the theory to alternative parameter choices. We also discuss how our approach complements the linear coupling technique. Our combination of perspectives leads to a better understanding of accelerated variance-reduced stochastic methods for finite-sum problems.

Analysis of Approximate Stochastic Gradient Using Quadratic Constraints and Sequential Semidefinite Programs

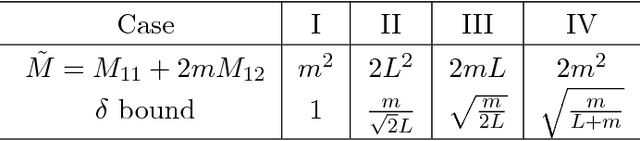
We present convergence rate analysis for the approximate stochastic gradient method, where individual gradient updates are corrupted by computation errors. We develop stochastic quadratic constraints to formulate a small linear matrix inequality (LMI) whose feasible set characterizes convergence properties of the approximate stochastic gradient. Based on this LMI condition, we develop a sequential minimization approach to analyze the intricate trade-offs that couple stepsize selection, convergence rate, optimization accuracy, and robustness to gradient inaccuracy. We also analytically solve this LMI condition and obtain theoretical formulas that quantify the convergence properties of the approximate stochastic gradient under various assumptions on the loss functions.