Near-Optimal Private Linear Regression via Iterative Hessian Mixing

We study differentially private ordinary least squares (DP-OLS) with bounded data. The dominant approach, adaptive sufficient-statistics perturbation (AdaSSP), adds an adaptively chosen perturbation to the sufficient statistics, namely, the matrix $X^{\top}X$ and the vector $X^{\top}Y$, and is known to achieve near-optimal accuracy and to have strong empirical performance. In contrast, methods that rely on Gaussian-sketching, which ensure differential privacy by pre-multiplying the data with a random Gaussian matrix, are widely used in federated and distributed regression, yet remain relatively uncommon for DP-OLS. In this work, we introduce the iterative Hessian mixing, a novel DP-OLS algorithm that relies on Gaussian sketches and is inspired by the iterative Hessian sketch algorithm. We provide utility analysis for the iterative Hessian mixing as well as a new analysis for the previous methods that rely on Gaussian sketches. Then, we show that our new approach circumvents the intrinsic limitations of the prior methods and provides non-trivial improvements over AdaSSP. We conclude by running an extensive set of experiments across standard benchmarks to demonstrate further that our approach consistently outperforms these prior baselines.

Adaptive Kernel Selection for Stein Variational Gradient Descent

A central challenge in Bayesian inference is efficiently approximating posterior distributions. Stein Variational Gradient Descent (SVGD) is a popular variational inference method which transports a set of particles to approximate a target distribution. The SVGD dynamics are governed by a reproducing kernel Hilbert space (RKHS) and are highly sensitive to the choice of the kernel function, which directly influences both convergence and approximation quality. The commonly used median heuristic offers a simple approach for setting kernel bandwidths but lacks flexibility and often performs poorly, particularly in high-dimensional settings. In this work, we propose an alternative strategy for adaptively choosing kernel parameters over an abstract family of kernels. Recent convergence analyses based on the kernelized Stein discrepancy (KSD) suggest that optimizing the kernel parameters by maximizing the KSD can improve performance. Building on this insight, we introduce Adaptive SVGD (Ad-SVGD), a method that alternates between updating the particles via SVGD and adaptively tuning kernel bandwidths through gradient ascent on the KSD. We provide a simplified theoretical analysis that extends existing results on minimizing the KSD for fixed kernels to our adaptive setting, showing convergence properties for the maximal KSD over our kernel class. Our empirical results further support this intuition: Ad-SVGD consistently outperforms standard heuristics in a variety of tasks.

Aligning Evaluation with Clinical Priorities: Calibration, Label Shift, and Error Costs

Machine learning-based decision support systems are increasingly deployed in clinical settings, where probabilistic scoring functions are used to inform and prioritize patient management decisions. However, widely used scoring rules, such as accuracy and AUC-ROC, fail to adequately reflect key clinical priorities, including calibration, robustness to distributional shifts, and sensitivity to asymmetric error costs. In this work, we propose a principled yet practical evaluation framework for selecting calibrated thresholded classifiers that explicitly accounts for the uncertainty in class prevalences and domain-specific cost asymmetries often found in clinical settings. Building on the theory of proper scoring rules, particularly the Schervish representation, we derive an adjusted variant of cross-entropy (log score) that averages cost-weighted performance over clinically relevant ranges of class balance. The resulting evaluation is simple to apply, sensitive to clinical deployment conditions, and designed to prioritize models that are both calibrated and robust to real-world variations.

Semivalue-based data valuation is arbitrary and gameable

The game-theoretic notion of the semivalue offers a popular framework for credit attribution and data valuation in machine learning. Semivalues have been proposed for a variety of high-stakes decisions involving data, such as determining contributor compensation, acquiring data from external sources, or filtering out low-value datapoints. In these applications, semivalues depend on the specification of a utility function that maps subsets of data to a scalar score. While it is broadly agreed that this utility function arises from a composition of a learning algorithm and a performance metric, its actual instantiation involves numerous subtle modeling choices. We argue that this underspecification leads to varying degrees of arbitrariness in semivalue-based valuations. Small, but arguably reasonable changes to the utility function can induce substantial shifts in valuations across datapoints. Moreover, these valuation methodologies are also often gameable: low-cost adversarial strategies exist to exploit this ambiguity and systematically redistribute value among datapoints. Through theoretical constructions and empirical examples, we demonstrate that a bad-faith valuator can manipulate utility specifications to favor preferred datapoints, and that a good-faith valuator is left without principled guidance to justify any particular specification. These vulnerabilities raise ethical and epistemic concerns about the use of semivalues in several applications. We conclude by highlighting the burden of justification that semivalue-based approaches place on modelers and discuss important considerations for identifying appropriate uses.

The Gaussian Mixing Mechanism: Renyi Differential Privacy via Gaussian Sketches

Gaussian sketching, which consists of pre-multiplying the data with a random Gaussian matrix, is a widely used technique for multiple problems in data science and machine learning, with applications spanning computationally efficient optimization, coded computing, and federated learning. This operation also provides differential privacy guarantees due to its inherent randomness. In this work, we revisit this operation through the lens of Renyi Differential Privacy (RDP), providing a refined privacy analysis that yields significantly tighter bounds than prior results. We then demonstrate how this improved analysis leads to performance improvement in different linear regression settings, establishing theoretical utility guarantees. Empirically, our methods improve performance across multiple datasets and, in several cases, reduce runtime.

A Consequentialist Critique of Binary Classification Evaluation Practices

ML-supported decisions, such as ordering tests or determining preventive custody, often involve binary classification based on probabilistic forecasts. Evaluation frameworks for such forecasts typically consider whether to prioritize independent-decision metrics (e.g., Accuracy) or top-K metrics (e.g., Precision@K), and whether to focus on fixed thresholds or threshold-agnostic measures like AUC-ROC. We highlight that a consequentialist perspective, long advocated by decision theorists, should naturally favor evaluations that support independent decisions using a mixture of thresholds given their prevalence, such as Brier scores and Log loss. However, our empirical analysis reveals a strong preference for top-K metrics or fixed thresholds in evaluations at major conferences like ICML, FAccT, and CHIL. To address this gap, we use this decision-theoretic framework to map evaluation metrics to their optimal use cases, along with a Python package, briertools, to promote the broader adoption of Brier scores. In doing so, we also uncover new theoretical connections, including a reconciliation between the Brier Score and Decision Curve Analysis, which clarifies and responds to a longstanding critique by (Assel, et al. 2017) regarding the clinical utility of proper scoring rules.

Unstable Unlearning: The Hidden Risk of Concept Resurgence in Diffusion Models

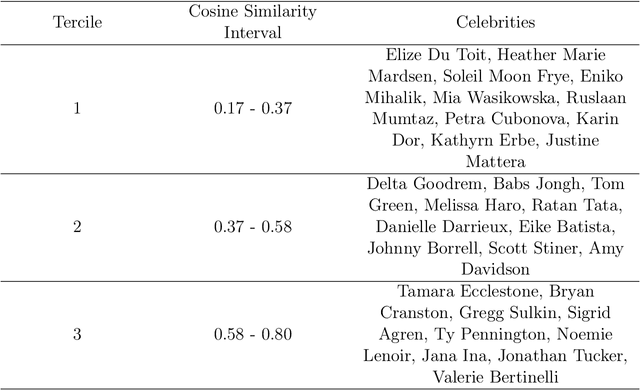
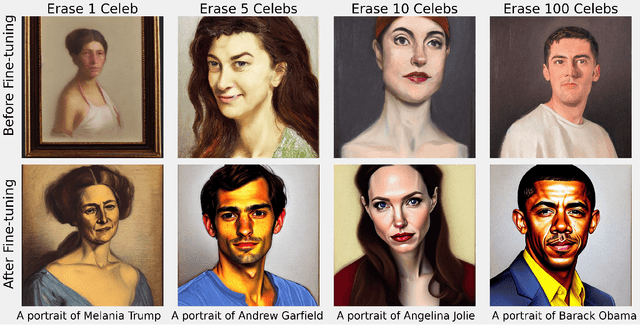
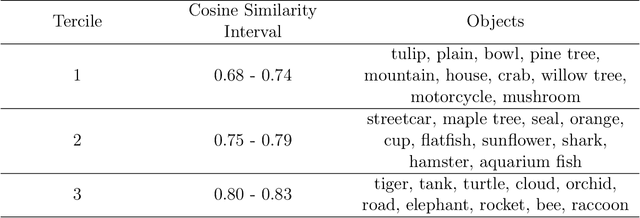
Text-to-image diffusion models rely on massive, web-scale datasets. Training them from scratch is computationally expensive, and as a result, developers often prefer to make incremental updates to existing models. These updates often compose fine-tuning steps (to learn new concepts or improve model performance) with "unlearning" steps (to "forget" existing concepts, such as copyrighted works or explicit content). In this work, we demonstrate a critical and previously unknown vulnerability that arises in this paradigm: even under benign, non-adversarial conditions, fine-tuning a text-to-image diffusion model on seemingly unrelated images can cause it to "relearn" concepts that were previously "unlearned." We comprehensively investigate the causes and scope of this phenomenon, which we term concept resurgence, by performing a series of experiments which compose "mass concept erasure" (the current state of the art for unlearning in text-to-image diffusion models (Lu et al., 2024)) with subsequent fine-tuning of Stable Diffusion v1.4. Our findings underscore the fragility of composing incremental model updates, and raise serious new concerns about current approaches to ensuring the safety and alignment of text-to-image diffusion models.

Adaptive Backtracking For Faster Optimization

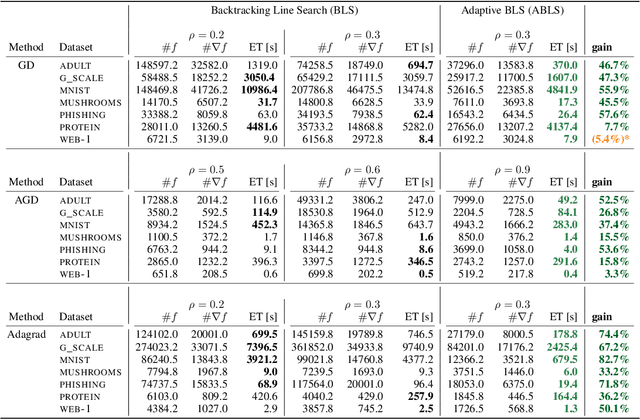
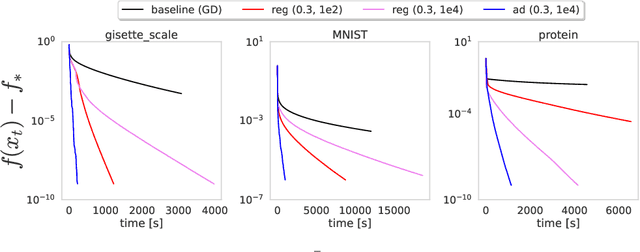
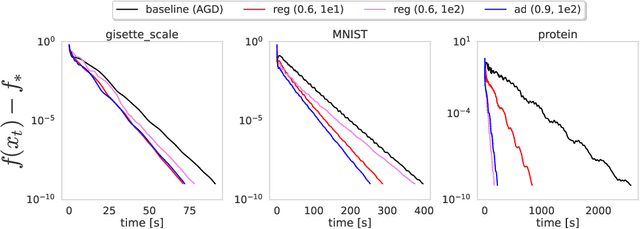
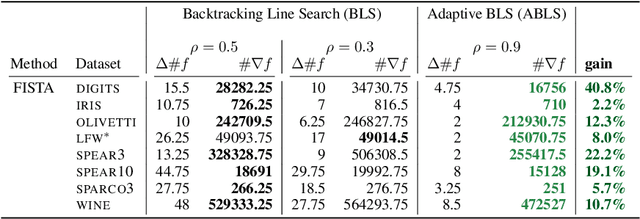
Backtracking line search is foundational in numerical optimization. The basic idea is to adjust the step size of an algorithm by a constant factor until some chosen criterion (e.g. Armijo, Goldstein, Descent Lemma) is satisfied. We propose a new way for adjusting step sizes, replacing the constant factor used in regular backtracking with one that takes into account the degree to which the chosen criterion is violated, without additional computational burden. For convex problems, we prove adaptive backtracking requires fewer adjustments to produce a feasible step size than regular backtracking does for two popular line search criteria: the Armijo condition and the descent lemma. For nonconvex smooth problems, we additionally prove adaptive backtracking enjoys the same guarantees of regular backtracking. Finally, we perform a variety of experiments on over fifteen real world datasets, all of which confirm that adaptive backtracking often leads to significantly faster optimization.

Algorithms that Approximate Data Removal: New Results and Limitations

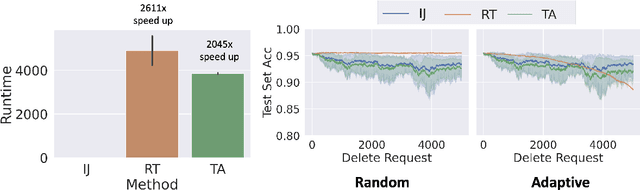
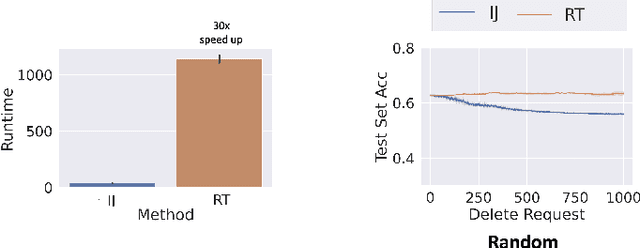
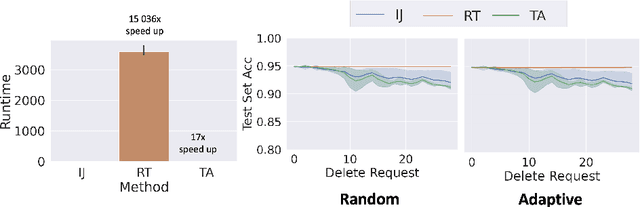
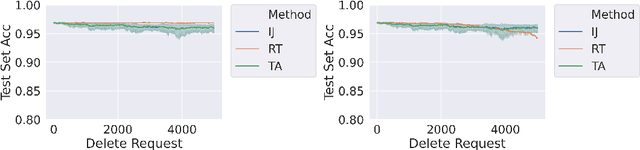
We study the problem of deleting user data from machine learning models trained using empirical risk minimization. Our focus is on learning algorithms which return the empirical risk minimizer and approximate unlearning algorithms that comply with deletion requests that come streaming minibatches. Leveraging the infintesimal jacknife, we develop an online unlearning algorithm that is both computationally and memory efficient. Unlike prior memory efficient unlearning algorithms, we target models that minimize objectives with non-smooth regularizers, such as the commonly used $\ell_1$, elastic net, or nuclear norm penalties. We also provide generalization, deletion capacity, and unlearning guarantees that are consistent with state of the art methods. Across a variety of benchmark datasets, our algorithm empirically improves upon the runtime of prior methods while maintaining the same memory requirements and test accuracy. Finally, we open a new direction of inquiry by proving that all approximate unlearning algorithms introduced so far fail to unlearn in problem settings where common hyperparameter tuning methods, such as cross-validation, have been used to select models.

The Marginal Value of Adaptive Gradient Methods in Machine Learning

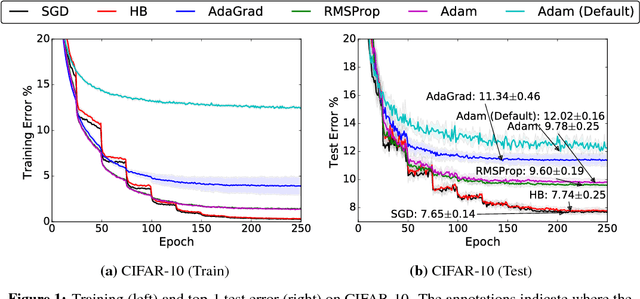
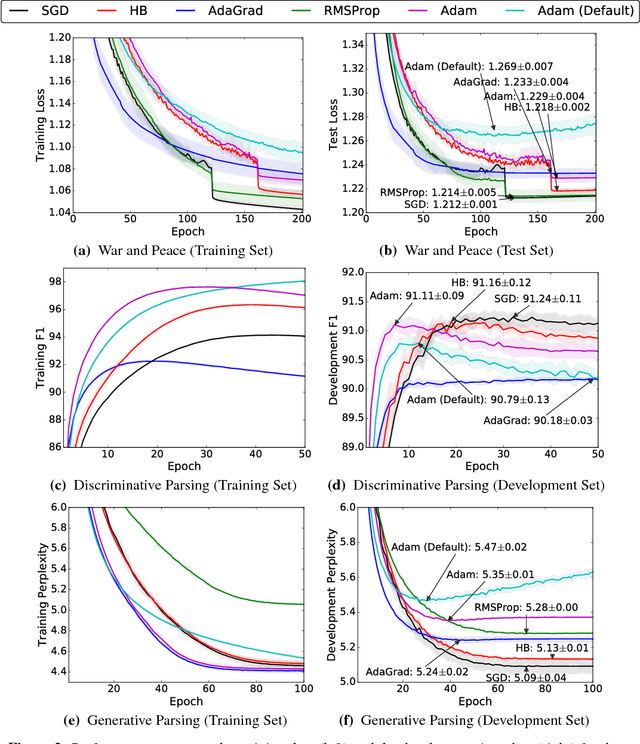
Adaptive optimization methods, which perform local optimization with a metric constructed from the history of iterates, are becoming increasingly popular for training deep neural networks. Examples include AdaGrad, RMSProp, and Adam. We show that for simple overparameterized problems, adaptive methods often find drastically different solutions than gradient descent (GD) or stochastic gradient descent (SGD). We construct an illustrative binary classification problem where the data is linearly separable, GD and SGD achieve zero test error, and AdaGrad, Adam, and RMSProp attain test errors arbitrarily close to half. We additionally study the empirical generalization capability of adaptive methods on several state-of-the-art deep learning models. We observe that the solutions found by adaptive methods generalize worse (often significantly worse) than SGD, even when these solutions have better training performance. These results suggest that practitioners should reconsider the use of adaptive methods to train neural networks.