How Well Can Differential Privacy Be Audited in One Run?

Recent methods for auditing the privacy of machine learning algorithms have improved computational efficiency by simultaneously intervening on multiple training examples in a single training run. Steinke et al. (2024) prove that one-run auditing indeed lower bounds the true privacy parameter of the audited algorithm, and give impressive empirical results. Their work leaves open the question of how precisely one-run auditing can uncover the true privacy parameter of an algorithm, and how that precision depends on the audited algorithm. In this work, we characterize the maximum achievable efficacy of one-run auditing and show that one-run auditing can only perfectly uncover the true privacy parameters of algorithms whose structure allows the effects of individual data elements to be isolated. Our characterization helps reveal how and when one-run auditing is still a promising technique for auditing real machine learning algorithms, despite these fundamental gaps.

Privacy amplification by random allocation

We consider the privacy guarantees of an algorithm in which a user's data is used in $k$ steps randomly and uniformly chosen from a sequence (or set) of $t$ differentially private steps. We demonstrate that the privacy guarantees of this sampling scheme can be upper bound by the privacy guarantees of the well-studied independent (or Poisson) subsampling in which each step uses the user's data with probability $(1+ o(1))k/t $. Further, we provide two additional analysis techniques that lead to numerical improvements in some parameter regimes. The case of $k=1$ has been previously studied in the context of DP-SGD in Balle et al. (2020) and very recently in Chua et al. (2024). Privacy analysis of Balle et al. (2020) relies on privacy amplification by shuffling which leads to overly conservative bounds. Privacy analysis of Chua et al. (2024a) relies on Monte Carlo simulations that are computationally prohibitive in many practical scenarios and have additional inherent limitations.

Generalization in the Face of Adaptivity: A Bayesian Perspective

Repeated use of a data sample via adaptively chosen queries can rapidly lead to overfitting, wherein the issued queries yield answers on the sample that differ wildly from the values of those queries on the underlying data distribution. Differential privacy provides a tool to ensure generalization despite adaptively-chosen queries, but its worst-case nature means that it cannot, for example, yield improved results for low-variance queries. In this paper, we give a simple new characterization that illuminates the core problem of adaptive data analysis. We show explicitly that the harms of adaptivity come from the covariance between the behavior of future queries and a Bayes factor-based measure of how much information about the data sample was encoded in the responses given to past queries. We leverage this intuition to introduce a new stability notion; we then use it to prove new generalization results for the most basic noise-addition mechanisms (Laplace and Gaussian noise addition), with guarantees that scale with the variance of the queries rather than the square of their range. Our characterization opens the door to new insights and new algorithms for the fundamental problem of achieving generalization in adaptive data analysis.

A New Analysis of Differential Privacy's Generalization Guarantees

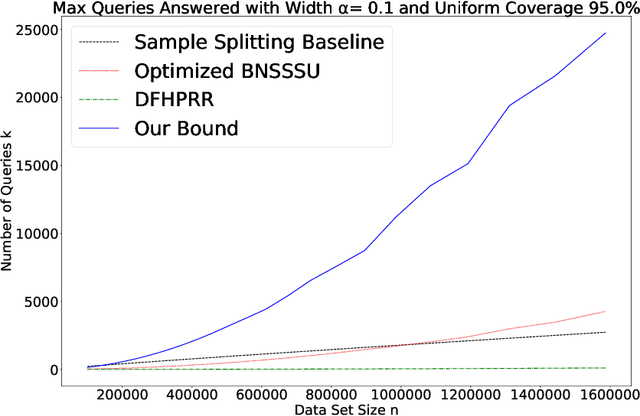
We give a new proof of the "transfer theorem" underlying adaptive data analysis: that any mechanism for answering adaptively chosen statistical queries that is differentially private and sample-accurate is also accurate out-of-sample. Our new proof is elementary and gives structural insights that we expect will be useful elsewhere. We show: 1) that differential privacy ensures that the expectation of any query on the posterior distribution on datasets induced by the transcript of the interaction is close to its true value on the data distribution, and 2) sample accuracy on its own ensures that any query answer produced by the mechanism is close to its posterior expectation with high probability. This second claim follows from a thought experiment in which we imagine that the dataset is resampled from the posterior distribution after the mechanism has committed to its answers. The transfer theorem then follows by summing these two bounds, and in particular, avoids the "monitor argument" used to derive high probability bounds in prior work. An upshot of our new proof technique is that the concrete bounds we obtain are substantially better than the best previously known bounds, even though the improvements are in the constants, rather than the asymptotics (which are known to be tight). As we show, our new bounds outperform the naive "sample-splitting" baseline at dramatically smaller dataset sizes compared to the previous state of the art, bringing techniques from this literature closer to practicality.

A necessary and sufficient stability notion for adaptive generalization

We introduce a new notion of the stability of computations, which holds under post-processing and adaptive composition, and show that the notion is both necessary and sufficient to ensure generalization in the face of adaptivity, for any computations that respond to bounded-sensitivity linear queries while providing accuracy with respect to the data sample set. The stability notion is based on quantifying the effect of observing a computation's outputs on the posterior over the data sample elements. We show a separation between this stability notion and previously studied notions.