Near-Optimal Private Linear Regression via Iterative Hessian Mixing

We study differentially private ordinary least squares (DP-OLS) with bounded data. The dominant approach, adaptive sufficient-statistics perturbation (AdaSSP), adds an adaptively chosen perturbation to the sufficient statistics, namely, the matrix $X^{\top}X$ and the vector $X^{\top}Y$, and is known to achieve near-optimal accuracy and to have strong empirical performance. In contrast, methods that rely on Gaussian-sketching, which ensure differential privacy by pre-multiplying the data with a random Gaussian matrix, are widely used in federated and distributed regression, yet remain relatively uncommon for DP-OLS. In this work, we introduce the iterative Hessian mixing, a novel DP-OLS algorithm that relies on Gaussian sketches and is inspired by the iterative Hessian sketch algorithm. We provide utility analysis for the iterative Hessian mixing as well as a new analysis for the previous methods that rely on Gaussian sketches. Then, we show that our new approach circumvents the intrinsic limitations of the prior methods and provides non-trivial improvements over AdaSSP. We conclude by running an extensive set of experiments across standard benchmarks to demonstrate further that our approach consistently outperforms these prior baselines.

Designing Algorithms for Entropic Optimal Transport from an Optimisation Perspective

In this work, we develop a collection of novel methods for the entropic-regularised optimal transport problem, which are inspired by existing mirror descent interpretations of the Sinkhorn algorithm used for solving this problem. These are fundamentally proposed from an optimisation perspective: either based on the associated semi-dual problem, or based on solving a non-convex constrained problem over subset of joint distributions. This optimisation viewpoint results in non-asymptotic rates of convergence for the proposed methods under minimal assumptions on the problem structure. We also propose a momentum-equipped method with provable accelerated guarantees through this viewpoint, akin to those in the Euclidean setting. The broader framework we develop based on optimisation over the joint distributions also finds an analogue in the dynamical Schr\"{o}dinger bridge problem.

The Gaussian Mixing Mechanism: Renyi Differential Privacy via Gaussian Sketches

Gaussian sketching, which consists of pre-multiplying the data with a random Gaussian matrix, is a widely used technique for multiple problems in data science and machine learning, with applications spanning computationally efficient optimization, coded computing, and federated learning. This operation also provides differential privacy guarantees due to its inherent randomness. In this work, we revisit this operation through the lens of Renyi Differential Privacy (RDP), providing a refined privacy analysis that yields significantly tighter bounds than prior results. We then demonstrate how this improved analysis leads to performance improvement in different linear regression settings, establishing theoretical utility guarantees. Empirically, our methods improve performance across multiple datasets and, in several cases, reduce runtime.

High-accuracy sampling from constrained spaces with the Metropolis-adjusted Preconditioned Langevin Algorithm

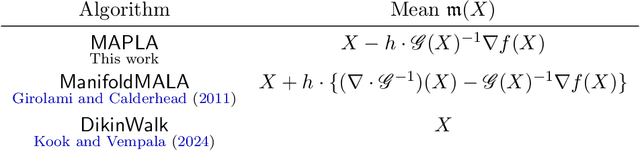
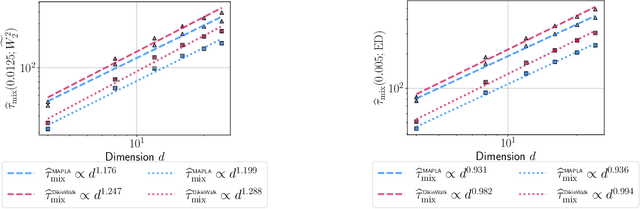
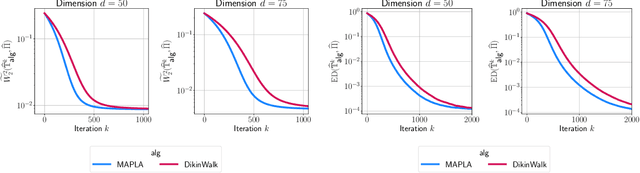
In this work, we propose a first-order sampling method called the Metropolis-adjusted Preconditioned Langevin Algorithm for approximate sampling from a target distribution whose support is a proper convex subset of $\mathbb{R}^{d}$. Our proposed method is the result of applying a Metropolis-Hastings filter to the Markov chain formed by a single step of the preconditioned Langevin algorithm with a metric $\mathscr{G}$, and is motivated by the natural gradient descent algorithm for optimisation. We derive non-asymptotic upper bounds for the mixing time of this method for sampling from target distributions whose potentials are bounded relative to $\mathscr{G}$, and for exponential distributions restricted to the support. Our analysis suggests that if $\mathscr{G}$ satisfies stronger notions of self-concordance introduced in Kook and Vempala (2024), then these mixing time upper bounds have a strictly better dependence on the dimension than when is merely self-concordant. We also provide numerical experiments that demonstrates the practicality of our proposed method. Our method is a high-accuracy sampler due to the polylogarithmic dependence on the error tolerance in our mixing time upper bounds.

Fast sampling from constrained spaces using the Metropolis-adjusted Mirror Langevin Algorithm

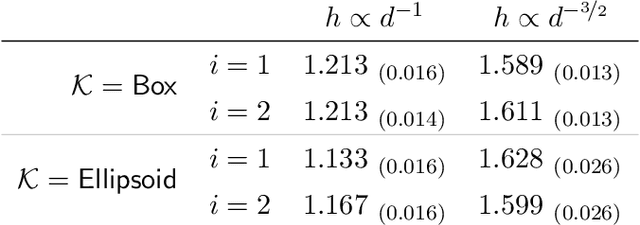
We propose a new method called the Metropolis-adjusted Mirror Langevin algorithm for approximate sampling from distributions whose support is a compact and convex set. This algorithm adds an accept-reject filter to the Markov chain induced by a single step of the mirror Langevin algorithm (Zhang et al., 2020), which is a basic discretisation of the mirror Langevin dynamics. Due to the inclusion of this filter, our method is unbiased relative to the target, while known discretisations of the mirror Langevin dynamics including the mirror Langevin algorithm have an asymptotic bias. We give upper bounds for the mixing time of the proposed algorithm when the potential is relatively smooth, convex, and Lipschitz with respect to a self-concordant mirror function. As a consequence of the reversibility of the Markov chain induced by the algorithm, we obtain an exponentially better dependence on the error tolerance for approximate sampling. We also present numerical experiments that corroborate our theoretical findings.

Sample Efficient Reinforcement Learning In Continuous State Spaces: A Perspective Beyond Linearity

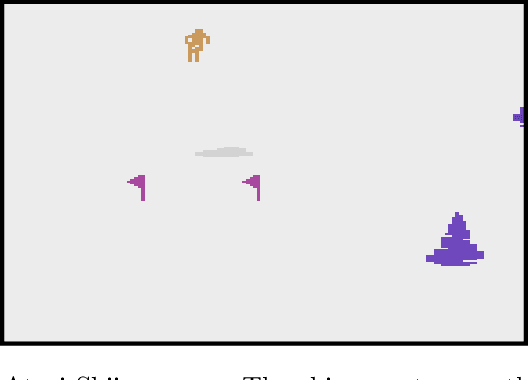
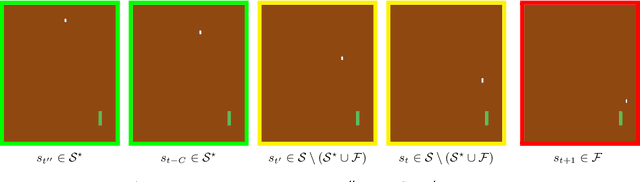
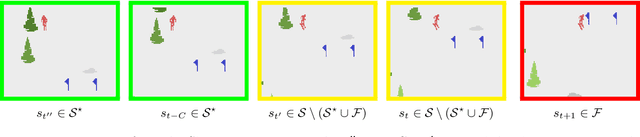
Reinforcement learning (RL) is empirically successful in complex nonlinear Markov decision processes (MDPs) with continuous state spaces. By contrast, the majority of theoretical RL literature requires the MDP to satisfy some form of linear structure, in order to guarantee sample efficient RL. Such efforts typically assume the transition dynamics or value function of the MDP are described by linear functions of the state features. To resolve this discrepancy between theory and practice, we introduce the Effective Planning Window (EPW) condition, a structural condition on MDPs that makes no linearity assumptions. We demonstrate that the EPW condition permits sample efficient RL, by providing an algorithm which provably solves MDPs satisfying this condition. Our algorithm requires minimal assumptions on the policy class, which can include multi-layer neural networks with nonlinear activation functions. Notably, the EPW condition is directly motivated by popular gaming benchmarks, and we show that many classic Atari games satisfy this condition. We additionally show the necessity of conditions like EPW, by demonstrating that simple MDPs with slight nonlinearities cannot be solved sample efficiently.

On the Analysis of Trajectories of Gradient Descent in the Optimization of Deep Neural Networks

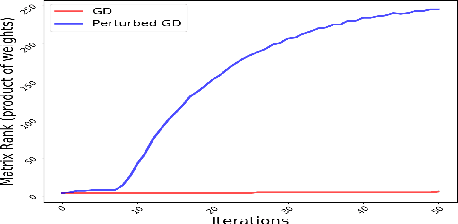
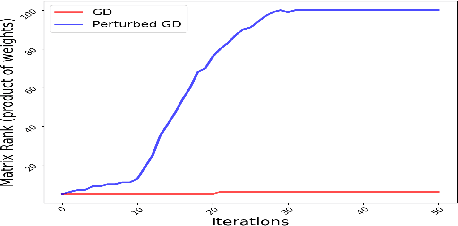
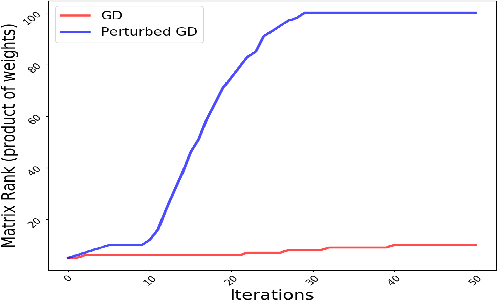
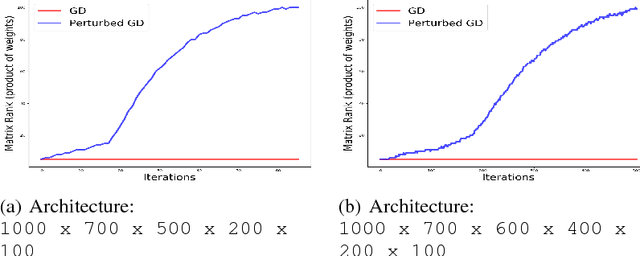
Theoretical analysis of the error landscape of deep neural networks has garnered significant interest in recent years. In this work, we theoretically study the importance of noise in the trajectories of gradient descent towards optimal solutions in multi-layer neural networks. We show that adding noise (in different ways) to a neural network while training increases the rank of the product of weight matrices of a multi-layer linear neural network. We thus study how adding noise can assist reaching a global optimum when the product matrix is full-rank (under certain conditions). We establish theoretical foundations between the noise induced into the neural network - either to the gradient, to the architecture, or to the input/output to a neural network - and the rank of product of weight matrices. We corroborate our theoretical findings with empirical results.

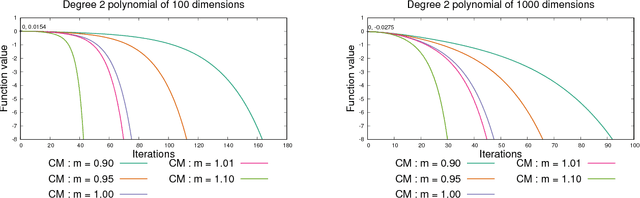
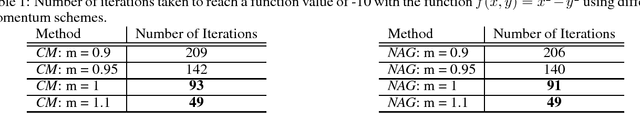
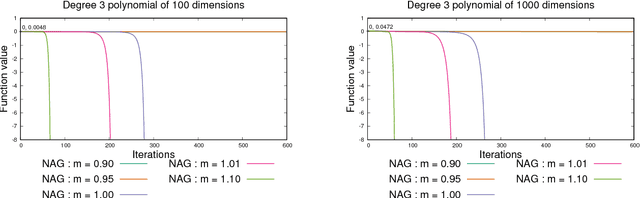
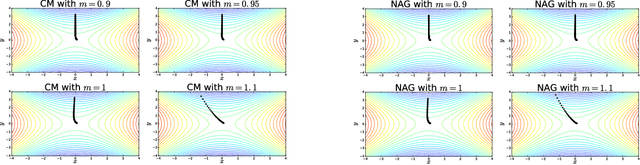
ADINE: An Adaptive Momentum Method for Stochastic Gradient Descent

Two major momentum-based techniques that have achieved tremendous success in optimization are Polyak's heavy ball method and Nesterov's accelerated gradient. A crucial step in all momentum-based methods is the choice of the momentum parameter $m$ which is always suggested to be set to less than $1$. Although the choice of $m < 1$ is justified only under very strong theoretical assumptions, it works well in practice even when the assumptions do not necessarily hold. In this paper, we propose a new momentum based method $\textit{ADINE}$, which relaxes the constraint of $m < 1$ and allows the learning algorithm to use adaptive higher momentum. We motivate our hypothesis on $m$ by experimentally verifying that a higher momentum ($\ge 1$) can help escape saddles much faster. Using this motivation, we propose our method $\textit{ADINE}$ that helps weigh the previous updates more (by setting the momentum parameter $> 1$), evaluate our proposed algorithm on deep neural networks and show that $\textit{ADINE}$ helps the learning algorithm to converge much faster without compromising on the generalization error.