High-accuracy sampling from constrained spaces with the Metropolis-adjusted Preconditioned Langevin Algorithm
Paper and Code
Dec 24, 2024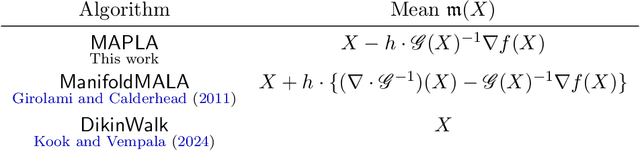
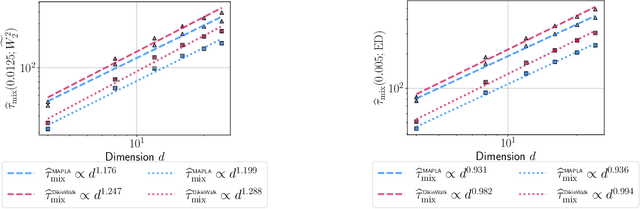

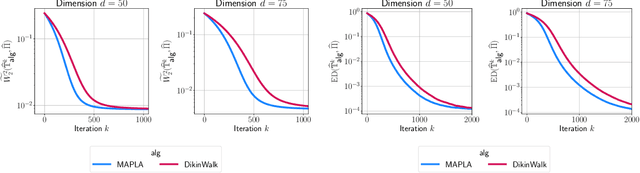
In this work, we propose a first-order sampling method called the Metropolis-adjusted Preconditioned Langevin Algorithm for approximate sampling from a target distribution whose support is a proper convex subset of $\mathbb{R}^{d}$. Our proposed method is the result of applying a Metropolis-Hastings filter to the Markov chain formed by a single step of the preconditioned Langevin algorithm with a metric $\mathscr{G}$, and is motivated by the natural gradient descent algorithm for optimisation. We derive non-asymptotic upper bounds for the mixing time of this method for sampling from target distributions whose potentials are bounded relative to $\mathscr{G}$, and for exponential distributions restricted to the support. Our analysis suggests that if $\mathscr{G}$ satisfies stronger notions of self-concordance introduced in Kook and Vempala (2024), then these mixing time upper bounds have a strictly better dependence on the dimension than when is merely self-concordant. We also provide numerical experiments that demonstrates the practicality of our proposed method. Our method is a high-accuracy sampler due to the polylogarithmic dependence on the error tolerance in our mixing time upper bounds.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge