High-accuracy sampling from constrained spaces with the Metropolis-adjusted Preconditioned Langevin Algorithm

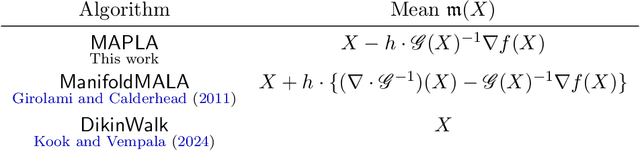
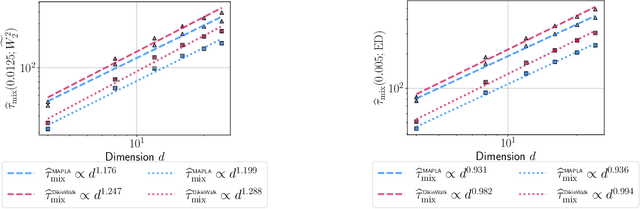
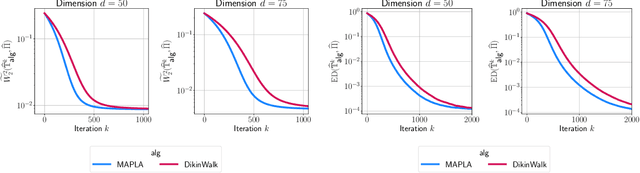
In this work, we propose a first-order sampling method called the Metropolis-adjusted Preconditioned Langevin Algorithm for approximate sampling from a target distribution whose support is a proper convex subset of $\mathbb{R}^{d}$. Our proposed method is the result of applying a Metropolis-Hastings filter to the Markov chain formed by a single step of the preconditioned Langevin algorithm with a metric $\mathscr{G}$, and is motivated by the natural gradient descent algorithm for optimisation. We derive non-asymptotic upper bounds for the mixing time of this method for sampling from target distributions whose potentials are bounded relative to $\mathscr{G}$, and for exponential distributions restricted to the support. Our analysis suggests that if $\mathscr{G}$ satisfies stronger notions of self-concordance introduced in Kook and Vempala (2024), then these mixing time upper bounds have a strictly better dependence on the dimension than when is merely self-concordant. We also provide numerical experiments that demonstrates the practicality of our proposed method. Our method is a high-accuracy sampler due to the polylogarithmic dependence on the error tolerance in our mixing time upper bounds.

Faster Machine Unlearning via Natural Gradient Descent

We address the challenge of efficiently and reliably deleting data from machine learning models trained using Empirical Risk Minimization (ERM), a process known as machine unlearning. To avoid retraining models from scratch, we propose a novel algorithm leveraging Natural Gradient Descent (NGD). Our theoretical framework ensures strong privacy guarantees for convex models, while a practical Min/Max optimization algorithm is developed for non-convex models. Comprehensive evaluations show significant improvements in privacy, computational efficiency, and generalization compared to state-of-the-art methods, advancing both the theoretical and practical aspects of machine unlearning.

Mean-field underdamped Langevin dynamics and its spacetime discretization

We propose a new method called the N-particle underdamped Langevin algorithm for optimizing a special class of non-linear functionals defined over the space of probability measures. Examples of problems with this formulation include training mean-field neural networks, maximum mean discrepancy minimization and kernel Stein discrepancy minimization. Our algorithm is based on a novel spacetime discretization of the mean-field underdamped Langevin dynamics, for which we provide a new, fast mixing guarantee. In addition, we demonstrate that our algorithm converges globally in total variation distance, bridging the theoretical gap between the dynamics and its practical implementation.

Fast sampling from constrained spaces using the Metropolis-adjusted Mirror Langevin Algorithm

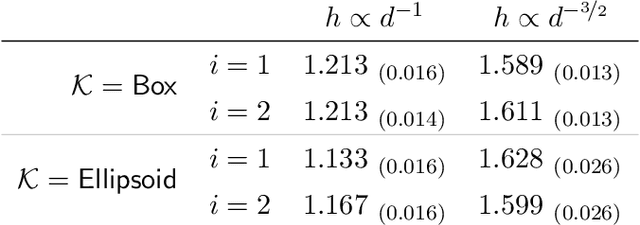
We propose a new method called the Metropolis-adjusted Mirror Langevin algorithm for approximate sampling from distributions whose support is a compact and convex set. This algorithm adds an accept-reject filter to the Markov chain induced by a single step of the mirror Langevin algorithm (Zhang et al., 2020), which is a basic discretisation of the mirror Langevin dynamics. Due to the inclusion of this filter, our method is unbiased relative to the target, while known discretisations of the mirror Langevin dynamics including the mirror Langevin algorithm have an asymptotic bias. We give upper bounds for the mixing time of the proposed algorithm when the potential is relatively smooth, convex, and Lipschitz with respect to a self-concordant mirror function. As a consequence of the reversibility of the Markov chain induced by the algorithm, we obtain an exponentially better dependence on the error tolerance for approximate sampling. We also present numerical experiments that corroborate our theoretical findings.

What is a Fair Diffusion Model? Designing Generative Text-To-Image Models to Incorporate Various Worldviews

Generative text-to-image (GTI) models produce high-quality images from short textual descriptions and are widely used in academic and creative domains. However, GTI models frequently amplify biases from their training data, often producing prejudiced or stereotypical images. Yet, current bias mitigation strategies are limited and primarily focus on enforcing gender parity across occupations. To enhance GTI bias mitigation, we introduce DiffusionWorldViewer, a tool to analyze and manipulate GTI models' attitudes, values, stories, and expectations of the world that impact its generated images. Through an interactive interface deployed as a web-based GUI and Jupyter Notebook plugin, DiffusionWorldViewer categorizes existing demographics of GTI-generated images and provides interactive methods to align image demographics with user worldviews. In a study with 13 GTI users, we find that DiffusionWorldViewer allows users to represent their varied viewpoints about what GTI outputs are fair and, in doing so, challenges current notions of fairness that assume a universal worldview.

Approximate Cross-validation: Guarantees for Model Assessment and Selection

Cross-validation (CV) is a popular approach for assessing and selecting predictive models. However, when the number of folds is large, CV suffers from a need to repeatedly refit a learning procedure on a large number of training datasets. Recent work in empirical risk minimization (ERM) approximates the expensive refitting with a single Newton step warm-started from the full training set optimizer. While this can greatly reduce runtime, several open questions remain including whether these approximations lead to faithful model selection and whether they are suitable for non-smooth objectives. We address these questions with three main contributions: (i) we provide uniform non-asymptotic, deterministic model assessment guarantees for approximate CV; (ii) we show that (roughly) the same conditions also guarantee model selection performance comparable to CV; (iii) we provide a proximal Newton extension of the approximate CV framework for non-smooth prediction problems and develop improved assessment guarantees for problems such as l1-regularized ERM.