A Deeper Look at the Hessian Eigenspectrum of Deep Neural Networks and its Applications to Regularization

Loss landscape analysis is extremely useful for a deeper understanding of the generalization ability of deep neural network models. In this work, we propose a layerwise loss landscape analysis where the loss surface at every layer is studied independently and also on how each correlates to the overall loss surface. We study the layerwise loss landscape by studying the eigenspectra of the Hessian at each layer. In particular, our results show that the layerwise Hessian geometry is largely similar to the entire Hessian. We also report an interesting phenomenon where the Hessian eigenspectrum of middle layers of the deep neural network are observed to most similar to the overall Hessian eigenspectrum. We also show that the maximum eigenvalue and the trace of the Hessian (both full network and layerwise) reduce as training of the network progresses. We leverage on these observations to propose a new regularizer based on the trace of the layerwise Hessian. Penalizing the trace of the Hessian at every layer indirectly forces Stochastic Gradient Descent to converge to flatter minima, which are shown to have better generalization performance. In particular, we show that such a layerwise regularizer can be leveraged to penalize the middlemost layers alone, which yields promising results. Our empirical studies on well-known deep nets across datasets support the claims of this work

DANTE: Deep AlterNations for Training nEural networks

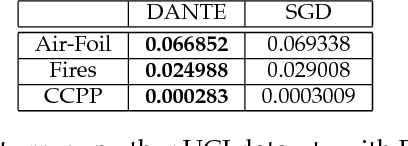
We present DANTE, a novel method for training neural networks using the alternating minimization principle. DANTE provides an alternate perspective to traditional gradient-based backpropagation techniques commonly used to train deep networks. It utilizes an adaptation of quasi-convexity to cast training a neural network as a bi-quasi-convex optimization problem. We show that for neural network configurations with both differentiable (e.g. sigmoid) and non-differentiable (e.g. ReLU) activation functions, we can perform the alternations very effectively. DANTE can also be extended to networks with multiple hidden layers. In experiments on standard datasets, neural networks trained using the proposed method were found to be very promising and competitive to traditional backpropagation techniques, both in terms of quality of the solution, as well as training speed.

On the Analysis of Trajectories of Gradient Descent in the Optimization of Deep Neural Networks

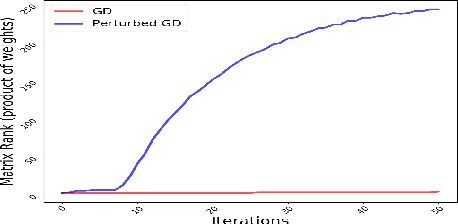
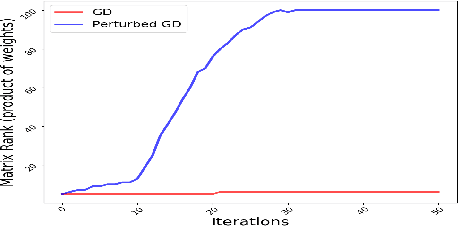
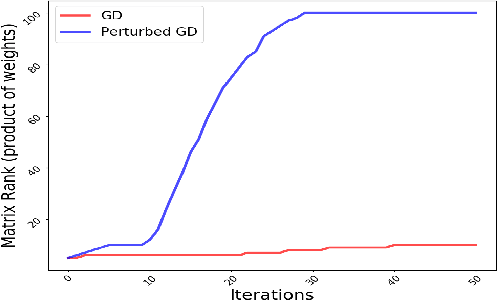
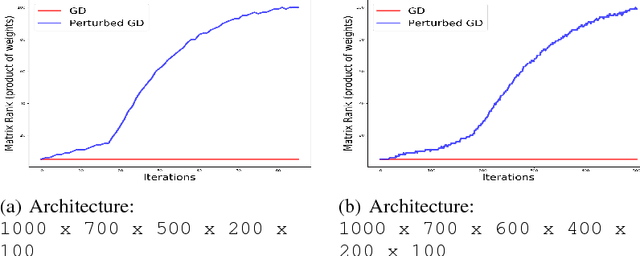
Theoretical analysis of the error landscape of deep neural networks has garnered significant interest in recent years. In this work, we theoretically study the importance of noise in the trajectories of gradient descent towards optimal solutions in multi-layer neural networks. We show that adding noise (in different ways) to a neural network while training increases the rank of the product of weight matrices of a multi-layer linear neural network. We thus study how adding noise can assist reaching a global optimum when the product matrix is full-rank (under certain conditions). We establish theoretical foundations between the noise induced into the neural network - either to the gradient, to the architecture, or to the input/output to a neural network - and the rank of product of weight matrices. We corroborate our theoretical findings with empirical results.

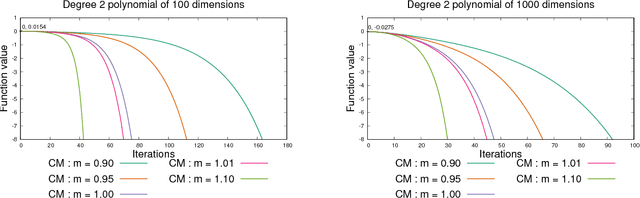
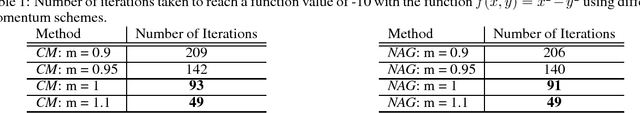
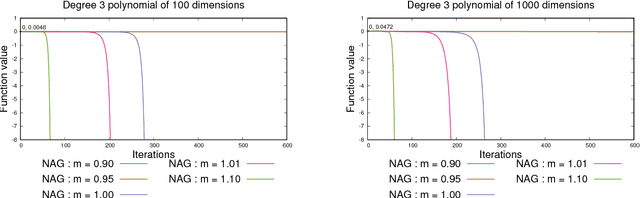
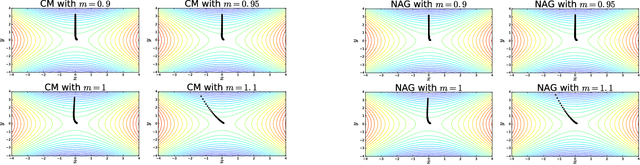
ADINE: An Adaptive Momentum Method for Stochastic Gradient Descent

Two major momentum-based techniques that have achieved tremendous success in optimization are Polyak's heavy ball method and Nesterov's accelerated gradient. A crucial step in all momentum-based methods is the choice of the momentum parameter $m$ which is always suggested to be set to less than $1$. Although the choice of $m < 1$ is justified only under very strong theoretical assumptions, it works well in practice even when the assumptions do not necessarily hold. In this paper, we propose a new momentum based method $\textit{ADINE}$, which relaxes the constraint of $m < 1$ and allows the learning algorithm to use adaptive higher momentum. We motivate our hypothesis on $m$ by experimentally verifying that a higher momentum ($\ge 1$) can help escape saddles much faster. Using this motivation, we propose our method $\textit{ADINE}$ that helps weigh the previous updates more (by setting the momentum parameter $> 1$), evaluate our proposed algorithm on deep neural networks and show that $\textit{ADINE}$ helps the learning algorithm to converge much faster without compromising on the generalization error.

Are Saddles Good Enough for Deep Learning?

Recent years have seen a growing interest in understanding deep neural networks from an optimization perspective. It is understood now that converging to low-cost local minima is sufficient for such models to become effective in practice. However, in this work, we propose a new hypothesis based on recent theoretical findings and empirical studies that deep neural network models actually converge to saddle points with high degeneracy. Our findings from this work are new, and can have a significant impact on the development of gradient descent based methods for training deep networks. We validated our hypotheses using an extensive experimental evaluation on standard datasets such as MNIST and CIFAR-10, and also showed that recent efforts that attempt to escape saddles finally converge to saddles with high degeneracy, which we define as `good saddles'. We also verified the famous Wigner's Semicircle Law in our experimental results.