Feature Generation for Long-tail Classification

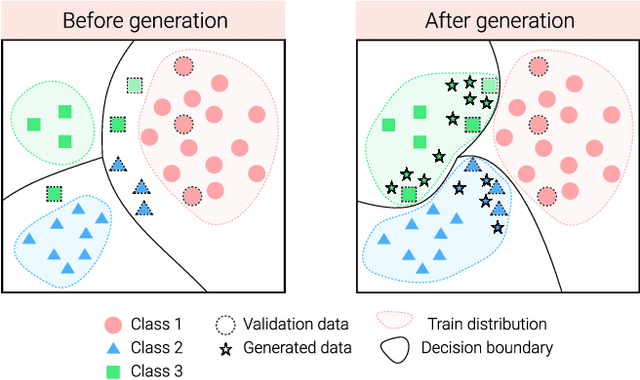
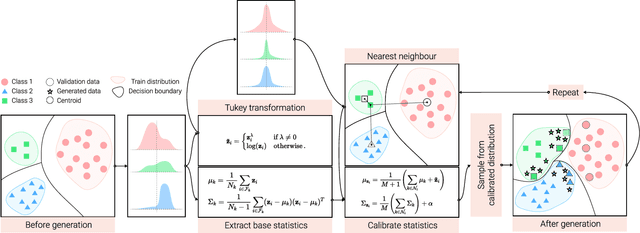
The visual world naturally exhibits an imbalance in the number of object or scene instances resulting in a \emph{long-tailed distribution}. This imbalance poses significant challenges for classification models based on deep learning. Oversampling instances of the tail classes attempts to solve this imbalance. However, the limited visual diversity results in a network with poor representation ability. A simple counter to this is decoupling the representation and classifier networks and using oversampling only to train the classifier. In this paper, instead of repeatedly re-sampling the same image (and thereby features), we explore a direction that attempts to generate meaningful features by estimating the tail category's distribution. Inspired by ideas from recent work on few-shot learning, we create calibrated distributions to sample additional features that are subsequently used to train the classifier. Through several experiments on the CIFAR-100-LT (long-tail) dataset with varying imbalance factors and on mini-ImageNet-LT (long-tail), we show the efficacy of our approach and establish a new state-of-the-art. We also present a qualitative analysis of generated features using t-SNE visualizations and analyze the nearest neighbors used to calibrate the tail class distributions. Our code is available at https://github.com/rahulvigneswaran/TailCalibX.

A Deeper Look at the Hessian Eigenspectrum of Deep Neural Networks and its Applications to Regularization

Loss landscape analysis is extremely useful for a deeper understanding of the generalization ability of deep neural network models. In this work, we propose a layerwise loss landscape analysis where the loss surface at every layer is studied independently and also on how each correlates to the overall loss surface. We study the layerwise loss landscape by studying the eigenspectra of the Hessian at each layer. In particular, our results show that the layerwise Hessian geometry is largely similar to the entire Hessian. We also report an interesting phenomenon where the Hessian eigenspectrum of middle layers of the deep neural network are observed to most similar to the overall Hessian eigenspectrum. We also show that the maximum eigenvalue and the trace of the Hessian (both full network and layerwise) reduce as training of the network progresses. We leverage on these observations to propose a new regularizer based on the trace of the layerwise Hessian. Penalizing the trace of the Hessian at every layer indirectly forces Stochastic Gradient Descent to converge to flatter minima, which are shown to have better generalization performance. In particular, we show that such a layerwise regularizer can be leveraged to penalize the middlemost layers alone, which yields promising results. Our empirical studies on well-known deep nets across datasets support the claims of this work