ADINE: An Adaptive Momentum Method for Stochastic Gradient Descent
Paper and Code
Dec 20, 2017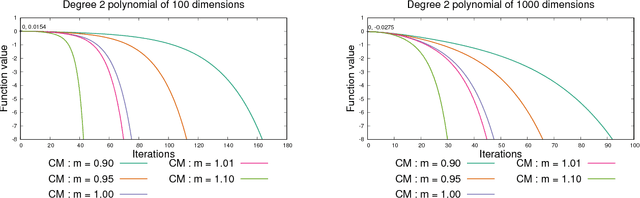
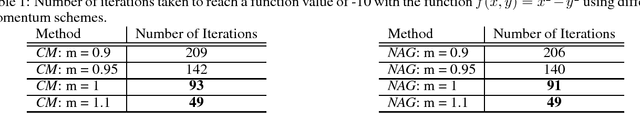
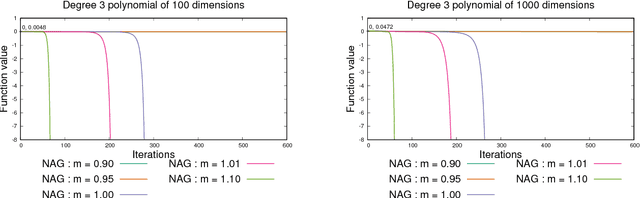
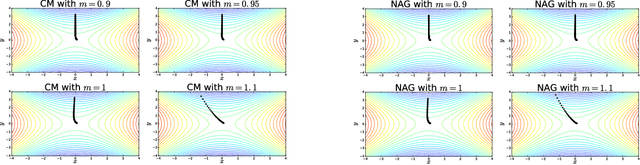
Two major momentum-based techniques that have achieved tremendous success in optimization are Polyak's heavy ball method and Nesterov's accelerated gradient. A crucial step in all momentum-based methods is the choice of the momentum parameter $m$ which is always suggested to be set to less than $1$. Although the choice of $m < 1$ is justified only under very strong theoretical assumptions, it works well in practice even when the assumptions do not necessarily hold. In this paper, we propose a new momentum based method $\textit{ADINE}$, which relaxes the constraint of $m < 1$ and allows the learning algorithm to use adaptive higher momentum. We motivate our hypothesis on $m$ by experimentally verifying that a higher momentum ($\ge 1$) can help escape saddles much faster. Using this motivation, we propose our method $\textit{ADINE}$ that helps weigh the previous updates more (by setting the momentum parameter $> 1$), evaluate our proposed algorithm on deep neural networks and show that $\textit{ADINE}$ helps the learning algorithm to converge much faster without compromising on the generalization error.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge