Beyond Parameter Count: Implicit Bias in Soft Mixture of Experts

The traditional viewpoint on Sparse Mixture of Experts (MoE) models is that instead of training a single large expert, which is computationally expensive, we can train many small experts. The hope is that if the total parameter count of the small experts equals that of the singular large expert, then we retain the representation power of the large expert while gaining computational tractability and promoting expert specialization. The recently introduced Soft MoE replaces the Sparse MoE's discrete routing mechanism with a differentiable gating function that smoothly mixes tokens. While this smooth gating function successfully mitigates the various training instabilities associated with Sparse MoE, it is unclear whether it induces implicit biases that affect Soft MoE's representation power or potential for expert specialization. We prove that Soft MoE with a single arbitrarily powerful expert cannot represent simple convex functions. This justifies that Soft MoE's success cannot be explained by the traditional viewpoint of many small experts collectively mimicking the representation power of a single large expert, and that multiple experts are actually necessary to achieve good representation power (even for a fixed total parameter count). Continuing along this line of investigation, we introduce a notion of expert specialization for Soft MoE, and while varying the number of experts yet fixing the total parameter count, we consider the following (computationally intractable) task. Given any input, how can we discover the expert subset that is specialized to predict this input's label? We empirically show that when there are many small experts, the architecture is implicitly biased in a fashion that allows us to efficiently approximate the specialized expert subset. Our method can be easily implemented to potentially reduce computation during inference.

Specifying and Solving Robust Empirical Risk Minimization Problems Using CVXPY

We consider robust empirical risk minimization (ERM), where model parameters are chosen to minimize the worst-case empirical loss when each data point varies over a given convex uncertainty set. In some simple cases, such problems can be expressed in an analytical form. In general the problem can be made tractable via dualization, which turns a min-max problem into a min-min problem. Dualization requires expertise and is tedious and error-prone. We demonstrate how CVXPY can be used to automate this dualization procedure in a user-friendly manner. Our framework allows practitioners to specify and solve robust ERM problems with a general class of convex losses, capturing many standard regression and classification problems. Users can easily specify any complex uncertainty set that is representable via disciplined convex programming (DCP) constraints.

Weighted Tallying Bandits: Overcoming Intractability via Repeated Exposure Optimality

In recommender system or crowdsourcing applications of online learning, a human's preferences or abilities are often a function of the algorithm's recent actions. Motivated by this, a significant line of work has formalized settings where an action's loss is a function of the number of times that action was recently played in the prior $m$ timesteps, where $m$ corresponds to a bound on human memory capacity. To more faithfully capture decay of human memory with time, we introduce the Weighted Tallying Bandit (WTB), which generalizes this setting by requiring that an action's loss is a function of a \emph{weighted} summation of the number of times that arm was played in the last $m$ timesteps. This WTB setting is intractable without further assumption. So we study it under Repeated Exposure Optimality (REO), a condition motivated by the literature on human physiology, which requires the existence of an action that when repetitively played will eventually yield smaller loss than any other sequence of actions. We study the minimization of the complete policy regret (CPR), which is the strongest notion of regret, in WTB under REO. Since $m$ is typically unknown, we assume we only have access to an upper bound $M$ on $m$. We show that for problems with $K$ actions and horizon $T$, a simple modification of the successive elimination algorithm has $O \left( \sqrt{KT} + (m+M)K \right)$ CPR. Interestingly, upto an additive (in lieu of mutliplicative) factor in $(m+M)K$, this recovers the classical guarantee for the simpler stochastic multi-armed bandit with traditional regret. We additionally show that in our setting, any algorithm will suffer additive CPR of $\Omega \left( mK + M \right)$, demonstrating our result is nearly optimal. Our algorithm is computationally efficient, and we experimentally demonstrate its practicality and superiority over natural baselines.

How Does Adaptive Optimization Impact Local Neural Network Geometry?

Adaptive optimization methods are well known to achieve superior convergence relative to vanilla gradient methods. The traditional viewpoint in optimization, particularly in convex optimization, explains this improved performance by arguing that, unlike vanilla gradient schemes, adaptive algorithms mimic the behavior of a second-order method by adapting to the global geometry of the loss function. We argue that in the context of neural network optimization, this traditional viewpoint is insufficient. Instead, we advocate for a local trajectory analysis. For iterate trajectories produced by running a generic optimization algorithm OPT, we introduce $R^{\text{OPT}}_{\text{med}}$, a statistic that is analogous to the condition number of the loss Hessian evaluated at the iterates. Through extensive experiments, we show that adaptive methods such as Adam bias the trajectories towards regions where $R^{\text{Adam}}_{\text{med}}$ is small, where one might expect faster convergence. By contrast, vanilla gradient methods like SGD bias the trajectories towards regions where $R^{\text{SGD}}_{\text{med}}$ is comparatively large. We complement these empirical observations with a theoretical result that provably demonstrates this phenomenon in the simplified setting of a two-layer linear network. We view our findings as evidence for the need of a new explanation of the success of adaptive methods, one that is different than the conventional wisdom.

Complete Policy Regret Bounds for Tallying Bandits

Policy regret is a well established notion of measuring the performance of an online learning algorithm against an adaptive adversary. We study restrictions on the adversary that enable efficient minimization of the \emph{complete policy regret}, which is the strongest possible version of policy regret. We identify a gap in the current theoretical understanding of what sorts of restrictions permit tractability in this challenging setting. To resolve this gap, we consider a generalization of the stochastic multi armed bandit, which we call the \emph{tallying bandit}. This is an online learning setting with an $m$-memory bounded adversary, where the average loss for playing an action is an unknown function of the number (or tally) of times that the action was played in the last $m$ timesteps. For tallying bandit problems with $K$ actions and time horizon $T$, we provide an algorithm that w.h.p achieves a complete policy regret guarantee of $\tilde{\mathcal{O}}(mK\sqrt{T})$, where the $\tilde{\mathcal{O}}$ notation hides only logarithmic factors. We additionally prove an $\tilde\Omega(\sqrt{m K T})$ lower bound on the expected complete policy regret of any tallying bandit algorithm, demonstrating the near optimality of our method.

Sample Efficient Reinforcement Learning In Continuous State Spaces: A Perspective Beyond Linearity

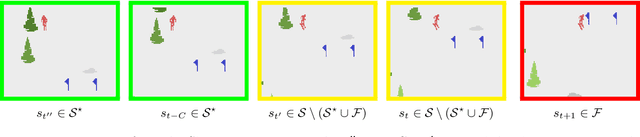
Reinforcement learning (RL) is empirically successful in complex nonlinear Markov decision processes (MDPs) with continuous state spaces. By contrast, the majority of theoretical RL literature requires the MDP to satisfy some form of linear structure, in order to guarantee sample efficient RL. Such efforts typically assume the transition dynamics or value function of the MDP are described by linear functions of the state features. To resolve this discrepancy between theory and practice, we introduce the Effective Planning Window (EPW) condition, a structural condition on MDPs that makes no linearity assumptions. We demonstrate that the EPW condition permits sample efficient RL, by providing an algorithm which provably solves MDPs satisfying this condition. Our algorithm requires minimal assumptions on the policy class, which can include multi-layer neural networks with nonlinear activation functions. Notably, the EPW condition is directly motivated by popular gaming benchmarks, and we show that many classic Atari games satisfy this condition. We additionally show the necessity of conditions like EPW, by demonstrating that simple MDPs with slight nonlinearities cannot be solved sample efficiently.

When Is Generalizable Reinforcement Learning Tractable?

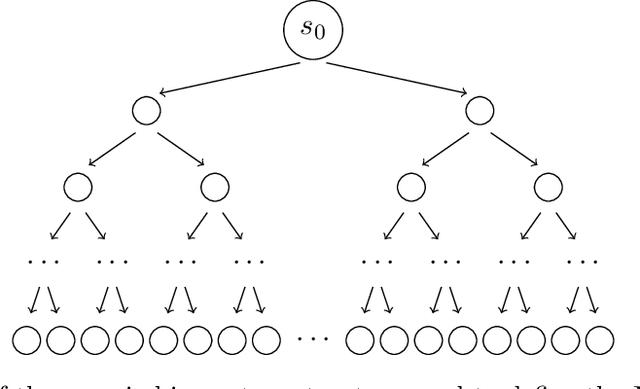
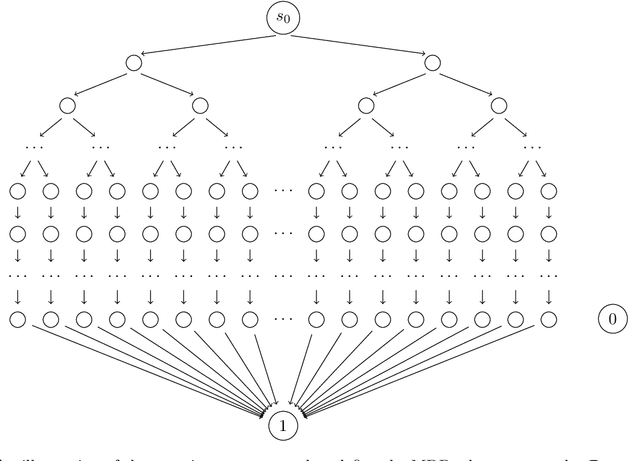
Agents trained by reinforcement learning (RL) often fail to generalize beyond the environment they were trained in, even when presented with new scenarios that seem very similar to the training environment. We study the query complexity required to train RL agents that can generalize to multiple environments. Intuitively, tractable generalization is only possible when the environments are similar or close in some sense. To capture this, we introduce Strong Proximity, a structural condition which precisely characterizes the relative closeness of different environments. We provide an algorithm which exploits Strong Proximity to provably and efficiently generalize. We also show that under a natural weakening of this condition, which we call Weak Proximity, RL can require query complexity that is exponential in the horizon to generalize. A key consequence of our theory is that even when the environments share optimal trajectories, and have highly similar reward and transition functions (as measured by classical metrics), tractable generalization is impossible.

Derivative-Free Methods for Policy Optimization: Guarantees for Linear Quadratic Systems

We study derivative-free methods for policy optimization over the class of linear policies. We focus on characterizing the convergence rate of these methods when applied to linear-quadratic systems, and study various settings of driving noise and reward feedback. We show that these methods provably converge to within any pre-specified tolerance of the optimal policy with a number of zero-order evaluations that is an explicit polynomial of the error tolerance, dimension, and curvature properties of the problem. Our analysis reveals some interesting differences between the settings of additive driving noise and random initialization, as well as the settings of one-point and two-point reward feedback. Our theory is corroborated by extensive simulations of derivative-free methods on these systems. Along the way, we derive convergence rates for stochastic zero-order optimization algorithms when applied to a certain class of non-convex problems.

An Efficient, Generalized Bellman Update For Cooperative Inverse Reinforcement Learning

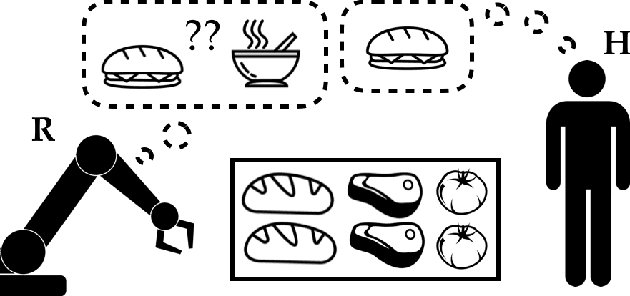
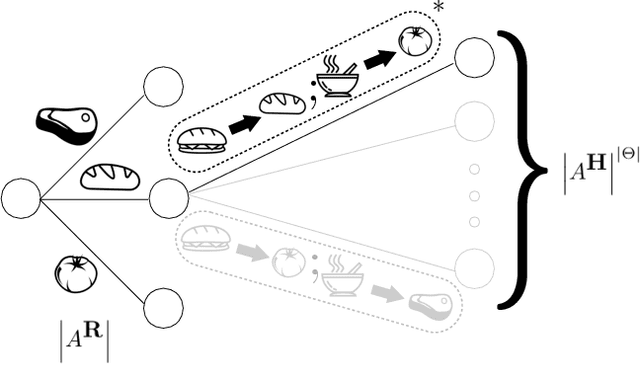
Our goal is for AI systems to correctly identify and act according to their human user's objectives. Cooperative Inverse Reinforcement Learning (CIRL) formalizes this value alignment problem as a two-player game between a human and robot, in which only the human knows the parameters of the reward function: the robot needs to learn them as the interaction unfolds. Previous work showed that CIRL can be solved as a POMDP, but with an action space size exponential in the size of the reward parameter space. In this work, we exploit a specific property of CIRL---the human is a full information agent---to derive an optimality-preserving modification to the standard Bellman update; this reduces the complexity of the problem by an exponential factor and allows us to relax CIRL's assumption of human rationality. We apply this update to a variety of POMDP solvers and find that it enables us to scale CIRL to non-trivial problems, with larger reward parameter spaces, and larger action spaces for both robot and human. In solutions to these larger problems, the human exhibits pedagogic (teaching) behavior, while the robot interprets it as such and attains higher value for the human.

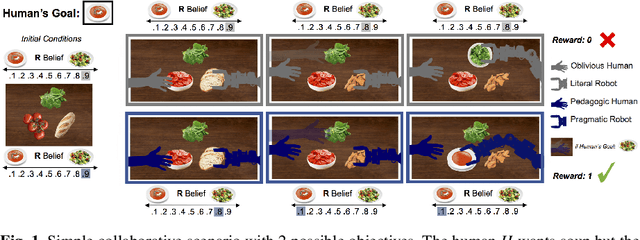
Pragmatic-Pedagogic Value Alignment

As intelligent systems gain autonomy and capability, it becomes vital to ensure that their objectives match those of their human users; this is known as the value-alignment problem. In robotics, value alignment is key to the design of collaborative robots that can integrate into human workflows, successfully inferring and adapting to their users' objectives as they go. We argue that a meaningful solution to value alignment must combine multi-agent decision theory with rich mathematical models of human cognition, enabling robots to tap into people's natural collaborative capabilities. We present a solution to the cooperative inverse reinforcement learning (CIRL) dynamic game based on well-established cognitive models of decision making and theory of mind. The solution captures a key reciprocity relation: the human will not plan her actions in isolation, but rather reason pedagogically about how the robot might learn from them; the robot, in turn, can anticipate this and interpret the human's actions pragmatically. To our knowledge, this work constitutes the first formal analysis of value alignment grounded in empirically validated cognitive models.