Exponentially Weighted Moving Models

An exponentially weighted moving model (EWMM) for a vector time series fits a new data model each time period, based on an exponentially fading loss function on past observed data. The well known and widely used exponentially weighted moving average (EWMA) is a special case that estimates the mean using a square loss function. For quadratic loss functions EWMMs can be fit using a simple recursion that updates the parameters of a quadratic function. For other loss functions, the entire past history must be stored, and the fitting problem grows in size as time increases. We propose a general method for computing an approximation of EWMM, which requires storing only a window of a fixed number of past samples, and uses an additional quadratic term to approximate the loss associated with the data before the window. This approximate EWMM relies on convex optimization, and solves problems that do not grow with time. We compare the estimates produced by our approximation with the estimates from the exact EWMM method.

Specifying and Solving Robust Empirical Risk Minimization Problems Using CVXPY

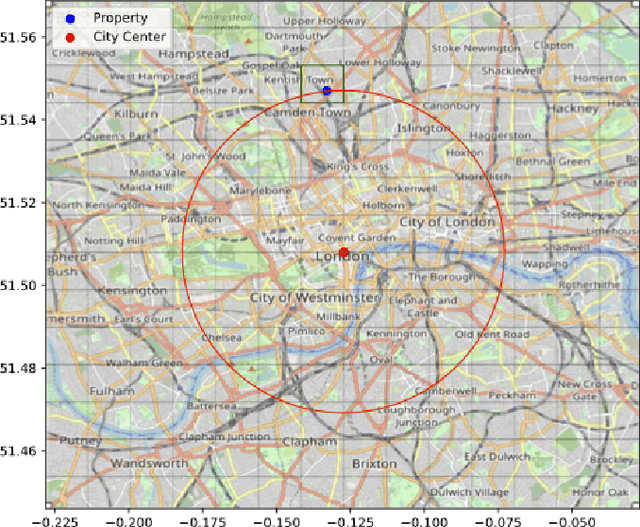
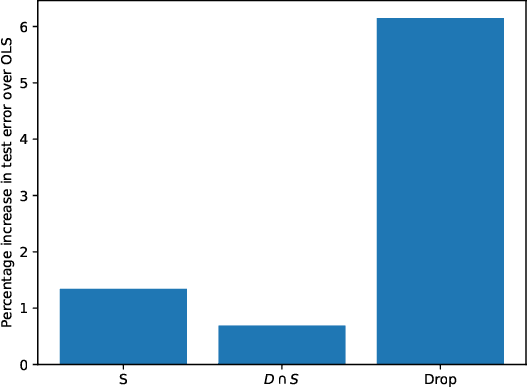
We consider robust empirical risk minimization (ERM), where model parameters are chosen to minimize the worst-case empirical loss when each data point varies over a given convex uncertainty set. In some simple cases, such problems can be expressed in an analytical form. In general the problem can be made tractable via dualization, which turns a min-max problem into a min-min problem. Dualization requires expertise and is tedious and error-prone. We demonstrate how CVXPY can be used to automate this dualization procedure in a user-friendly manner. Our framework allows practitioners to specify and solve robust ERM problems with a general class of convex losses, capturing many standard regression and classification problems. Users can easily specify any complex uncertainty set that is representable via disciplined convex programming (DCP) constraints.