Exponentially Weighted Moving Models
Paper and Code
Apr 11, 2024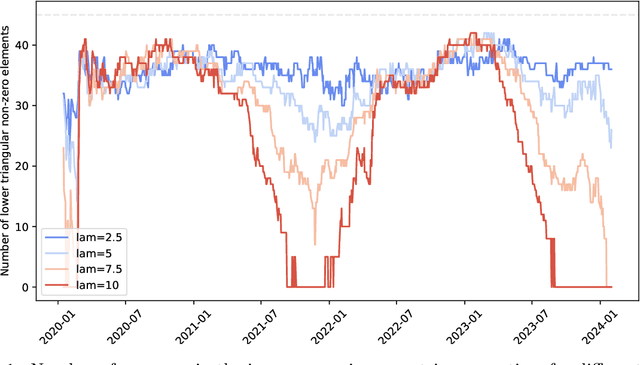

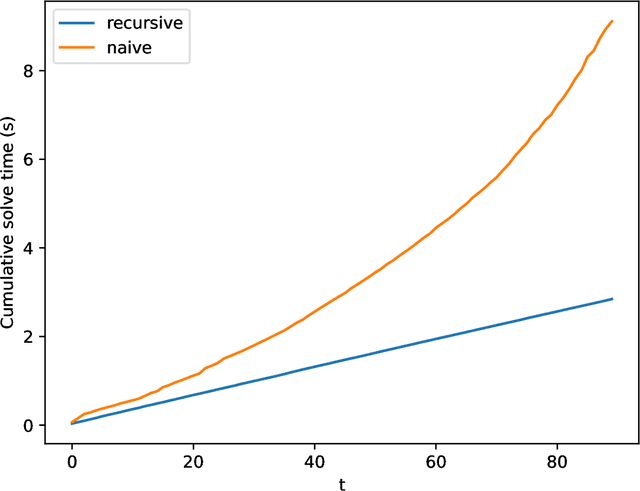
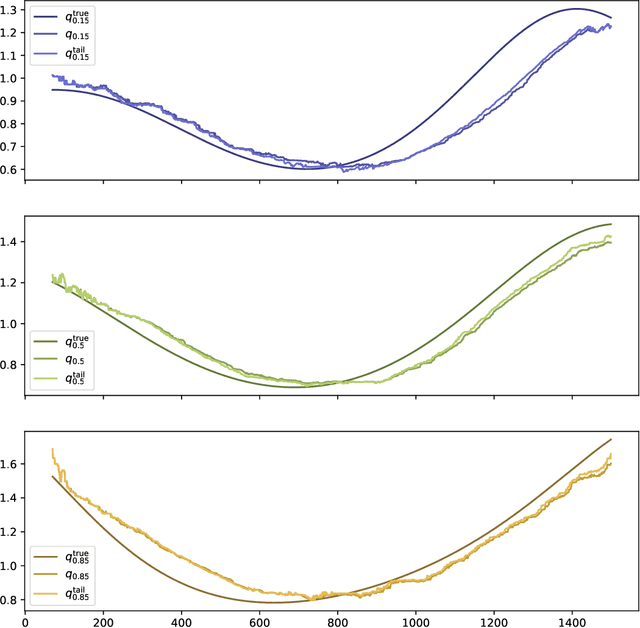
An exponentially weighted moving model (EWMM) for a vector time series fits a new data model each time period, based on an exponentially fading loss function on past observed data. The well known and widely used exponentially weighted moving average (EWMA) is a special case that estimates the mean using a square loss function. For quadratic loss functions EWMMs can be fit using a simple recursion that updates the parameters of a quadratic function. For other loss functions, the entire past history must be stored, and the fitting problem grows in size as time increases. We propose a general method for computing an approximation of EWMM, which requires storing only a window of a fixed number of past samples, and uses an additional quadratic term to approximate the loss associated with the data before the window. This approximate EWMM relies on convex optimization, and solves problems that do not grow with time. We compare the estimates produced by our approximation with the estimates from the exact EWMM method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge