Diff4Steer: Steerable Diffusion Prior for Generative Music Retrieval with Semantic Guidance

Modern music retrieval systems often rely on fixed representations of user preferences, limiting their ability to capture users' diverse and uncertain retrieval needs. To address this limitation, we introduce Diff4Steer, a novel generative retrieval framework that employs lightweight diffusion models to synthesize diverse seed embeddings from user queries that represent potential directions for music exploration. Unlike deterministic methods that map user query to a single point in embedding space, Diff4Steer provides a statistical prior on the target modality (audio) for retrieval, effectively capturing the uncertainty and multi-faceted nature of user preferences. Furthermore, Diff4Steer can be steered by image or text inputs, enabling more flexible and controllable music discovery combined with nearest neighbor search. Our framework outperforms deterministic regression methods and LLM-based generative retrieval baseline in terms of retrieval and ranking metrics, demonstrating its effectiveness in capturing user preferences, leading to more diverse and relevant recommendations. Listening examples are available at tinyurl.com/diff4steer.

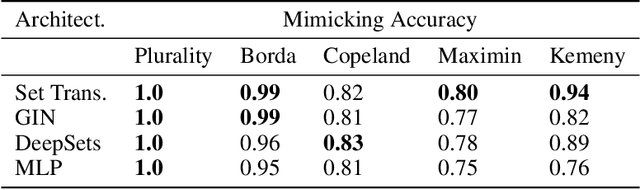
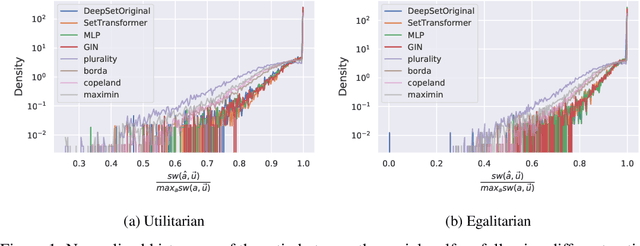
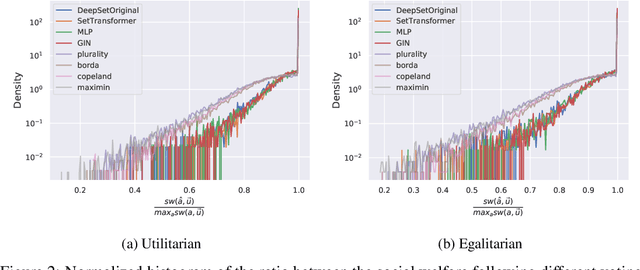
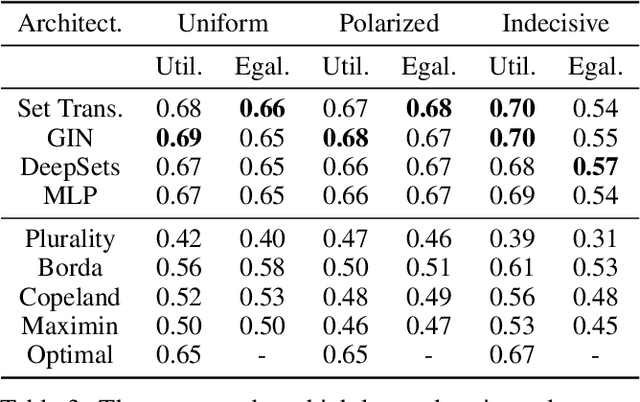
Learning to Elect

Voting systems have a wide range of applications including recommender systems, web search, product design and elections. Limited by the lack of general-purpose analytical tools, it is difficult to hand-engineer desirable voting rules for each use case. For this reason, it is appealing to automatically discover voting rules geared towards each scenario. In this paper, we show that set-input neural network architectures such as Set Transformers, fully-connected graph networks and DeepSets are both theoretically and empirically well-suited for learning voting rules. In particular, we show that these network models can not only mimic a number of existing voting rules to compelling accuracy --- both position-based (such as Plurality and Borda) and comparison-based (such as Kemeny, Copeland and Maximin) --- but also discover near-optimal voting rules that maximize different social welfare functions. Furthermore, the learned voting rules generalize well to different voter utility distributions and election sizes unseen during training.

A Unified Analysis of First-Order Methods for Smooth Games via Integral Quadratic Constraints

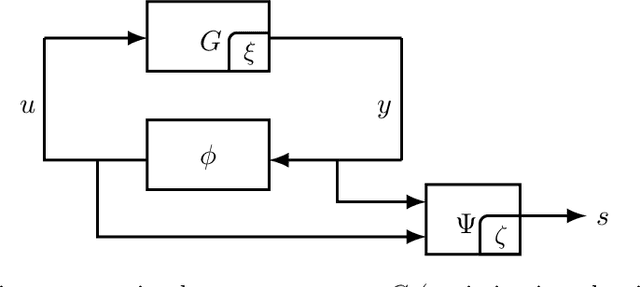
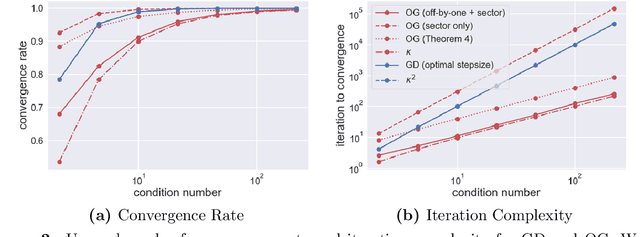
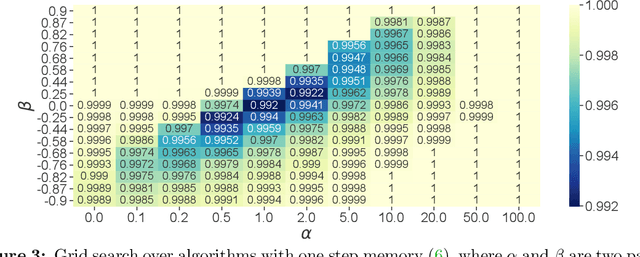
The theory of integral quadratic constraints (IQCs) allows the certification of exponential convergence of interconnected systems containing nonlinear or uncertain elements. In this work, we adapt the IQC theory to study first-order methods for smooth and strongly-monotone games and show how to design tailored quadratic constraints to get tight upper bounds of convergence rates. Using this framework, we recover the existing bound for the gradient method~(GD), derive sharper bounds for the proximal point method~(PPM) and optimistic gradient method~(OG), and provide \emph{for the first time} a global convergence rate for the negative momentum method~(NM) with an iteration complexity $\bigo(\kappa^{1.5})$, which matches its known lower bound. In addition, for time-varying systems, we prove that the gradient method with optimal step size achieves the fastest provable worst-case convergence rate with quadratic Lyapunov functions. Finally, we further extend our analysis to stochastic games and study the impact of multiplicative noise on different algorithms. We show that it is impossible for an algorithm with one step of memory to achieve acceleration if it only queries the gradient once per batch (in contrast with the stochastic strongly-convex optimization setting, where such acceleration has been demonstrated). However, we exhibit an algorithm which achieves acceleration with two gradient queries per batch.

Regularized linear autoencoders recover the principal components, eventually

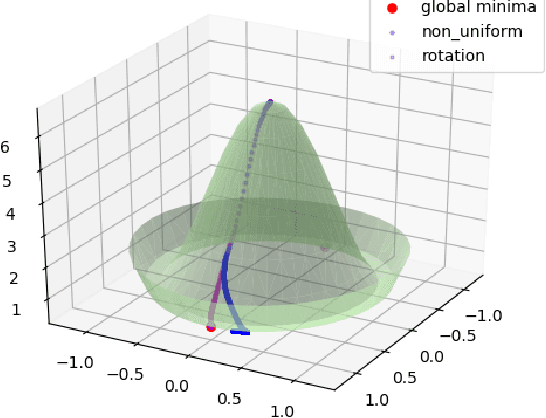
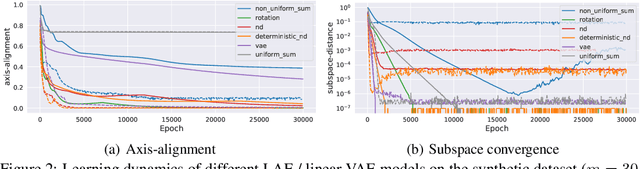
Our understanding of learning input-output relationships with neural nets has improved rapidly in recent years, but little is known about the convergence of the underlying representations, even in the simple case of linear autoencoders (LAEs). We show that when trained with proper regularization, LAEs can directly learn the optimal representation -- ordered, axis-aligned principal components. We analyze two such regularization schemes: non-uniform $\ell_2$ regularization and a deterministic variant of nested dropout [Rippel et al, ICML' 2014]. Though both regularization schemes converge to the optimal representation, we show that this convergence is slow due to ill-conditioning that worsens with increasing latent dimension. We show that the inefficiency of learning the optimal representation is not inevitable -- we present a simple modification to the gradient descent update that greatly speeds up convergence empirically.

Benchmarking Model-Based Reinforcement Learning

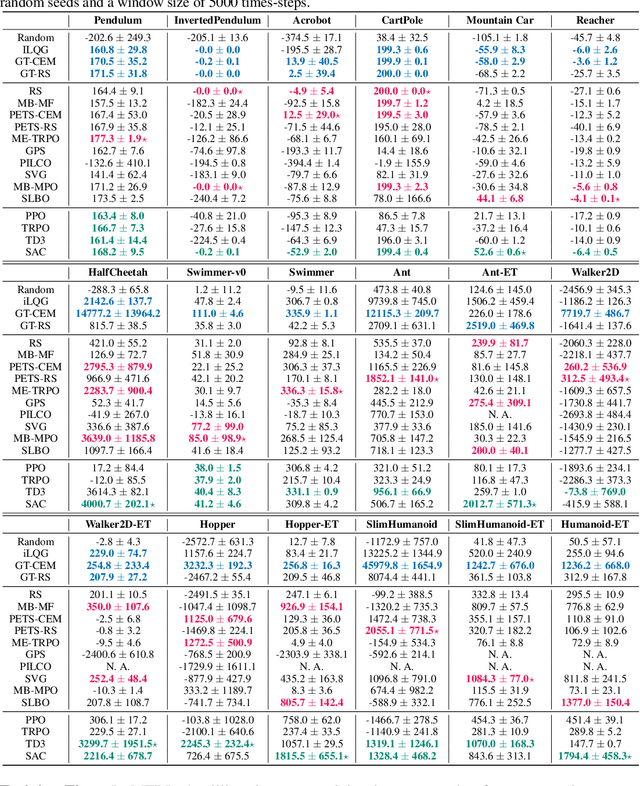
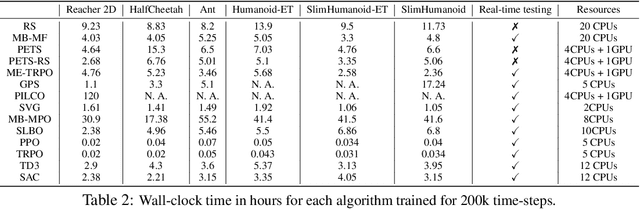
Model-based reinforcement learning (MBRL) is widely seen as having the potential to be significantly more sample efficient than model-free RL. However, research in model-based RL has not been very standardized. It is fairly common for authors to experiment with self-designed environments, and there are several separate lines of research, which are sometimes closed-sourced or not reproducible. Accordingly, it is an open question how these various existing MBRL algorithms perform relative to each other. To facilitate research in MBRL, in this paper we gather a wide collection of MBRL algorithms and propose over 18 benchmarking environments specially designed for MBRL. We benchmark these algorithms with unified problem settings, including noisy environments. Beyond cataloguing performance, we explore and unify the underlying algorithmic differences across MBRL algorithms. We characterize three key research challenges for future MBRL research: the dynamics bottleneck, the planning horizon dilemma, and the early-termination dilemma. Finally, to maximally facilitate future research on MBRL, we open-source our benchmark in http://www.cs.toronto.edu/~tingwuwang/mbrl.html.

TimbreTron: A WaveNet(CycleGAN(CQT(Audio))) Pipeline for Musical Timbre Transfer

In this work, we address the problem of musical timbre transfer, where the goal is to manipulate the timbre of a sound sample from one instrument to match another instrument while preserving other musical content, such as pitch, rhythm, and loudness. In principle, one could apply image-based style transfer techniques to a time-frequency representation of an audio signal, but this depends on having a representation that allows independent manipulation of timbre as well as high-quality waveform generation. We introduce TimbreTron, a method for musical timbre transfer which applies "image" domain style transfer to a time-frequency representation of the audio signal, and then produces a high-quality waveform using a conditional WaveNet synthesizer. We show that the Constant Q Transform (CQT) representation is particularly well-suited to convolutional architectures due to its approximate pitch equivariance. Based on human perceptual evaluations, we confirmed that TimbreTron recognizably transferred the timbre while otherwise preserving the musical content, for both monophonic and polyphonic samples.

Deep Neural Networks for Improved, Impromptu Trajectory Tracking of Quadrotors

Trajectory tracking control for quadrotors is important for applications ranging from surveying and inspection, to film making. However, designing and tuning classical controllers, such as proportional-integral-derivative (PID) controllers, to achieve high tracking precision can be time-consuming and difficult, due to hidden dynamics and other non-idealities. The Deep Neural Network (DNN), with its superior capability of approximating abstract, nonlinear functions, proposes a novel approach for enhancing trajectory tracking control. This paper presents a DNN-based algorithm as an add-on module that improves the tracking performance of a classical feedback controller. Given a desired trajectory, the DNNs provide a tailored reference input to the controller based on their gained experience. The input aims to achieve a unity map between the desired and the output trajectory. The motivation for this work is an interactive "fly-as-you-draw" application, in which a user draws a trajectory on a mobile device, and a quadrotor instantly flies that trajectory with the DNN-enhanced control system. Experimental results demonstrate that the proposed approach improves the tracking precision for user-drawn trajectories after the DNNs are trained on selected periodic trajectories, suggesting the method's potential in real-world applications. Tracking errors are reduced by around 40-50% for both training and testing trajectories from users, highlighting the DNNs' capability of generalizing knowledge.