TimbreTron: A WaveNet(CycleGAN(CQT(Audio))) Pipeline for Musical Timbre Transfer

In this work, we address the problem of musical timbre transfer, where the goal is to manipulate the timbre of a sound sample from one instrument to match another instrument while preserving other musical content, such as pitch, rhythm, and loudness. In principle, one could apply image-based style transfer techniques to a time-frequency representation of an audio signal, but this depends on having a representation that allows independent manipulation of timbre as well as high-quality waveform generation. We introduce TimbreTron, a method for musical timbre transfer which applies "image" domain style transfer to a time-frequency representation of the audio signal, and then produces a high-quality waveform using a conditional WaveNet synthesizer. We show that the Constant Q Transform (CQT) representation is particularly well-suited to convolutional architectures due to its approximate pitch equivariance. Based on human perceptual evaluations, we confirmed that TimbreTron recognizably transferred the timbre while otherwise preserving the musical content, for both monophonic and polyphonic samples.

The Reversible Residual Network: Backpropagation Without Storing Activations

Deep residual networks (ResNets) have significantly pushed forward the state-of-the-art on image classification, increasing in performance as networks grow both deeper and wider. However, memory consumption becomes a bottleneck, as one needs to store the activations in order to calculate gradients using backpropagation. We present the Reversible Residual Network (RevNet), a variant of ResNets where each layer's activations can be reconstructed exactly from the next layer's. Therefore, the activations for most layers need not be stored in memory during backpropagation. We demonstrate the effectiveness of RevNets on CIFAR-10, CIFAR-100, and ImageNet, establishing nearly identical classification accuracy to equally-sized ResNets, even though the activation storage requirements are independent of depth.

Measuring the reliability of MCMC inference with bidirectional Monte Carlo

Markov chain Monte Carlo (MCMC) is one of the main workhorses of probabilistic inference, but it is notoriously hard to measure the quality of approximate posterior samples. This challenge is particularly salient in black box inference methods, which can hide details and obscure inference failures. In this work, we extend the recently introduced bidirectional Monte Carlo technique to evaluate MCMC-based posterior inference algorithms. By running annealed importance sampling (AIS) chains both from prior to posterior and vice versa on simulated data, we upper bound in expectation the symmetrized KL divergence between the true posterior distribution and the distribution of approximate samples. We present Bounding Divergences with REverse Annealing (BREAD), a protocol for validating the relevance of simulated data experiments to real datasets, and integrate it into two probabilistic programming languages: WebPPL and Stan. As an example of how BREAD can be used to guide the design of inference algorithms, we apply it to study the effectiveness of different model representations in both WebPPL and Stan.

Sandwiching the marginal likelihood using bidirectional Monte Carlo

Computing the marginal likelihood (ML) of a model requires marginalizing out all of the parameters and latent variables, a difficult high-dimensional summation or integration problem. To make matters worse, it is often hard to measure the accuracy of one's ML estimates. We present bidirectional Monte Carlo, a technique for obtaining accurate log-ML estimates on data simulated from a model. This method obtains stochastic lower bounds on the log-ML using annealed importance sampling or sequential Monte Carlo, and obtains stochastic upper bounds by running these same algorithms in reverse starting from an exact posterior sample. The true value can be sandwiched between these two stochastic bounds with high probability. Using the ground truth log-ML estimates obtained from our method, we quantitatively evaluate a wide variety of existing ML estimators on several latent variable models: clustering, a low rank approximation, and a binary attributes model. These experiments yield insights into how to accurately estimate marginal likelihoods.

Accurate and Conservative Estimates of MRF Log-likelihood using Reverse Annealing

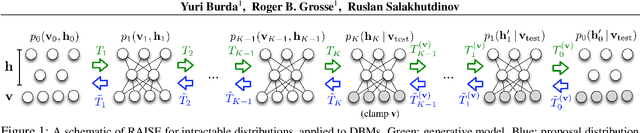
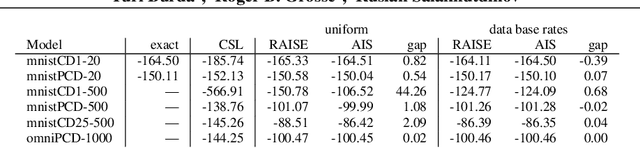
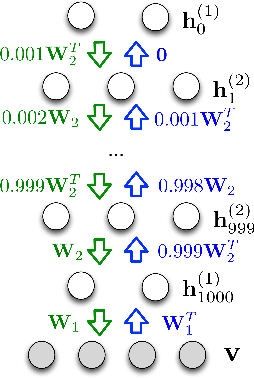
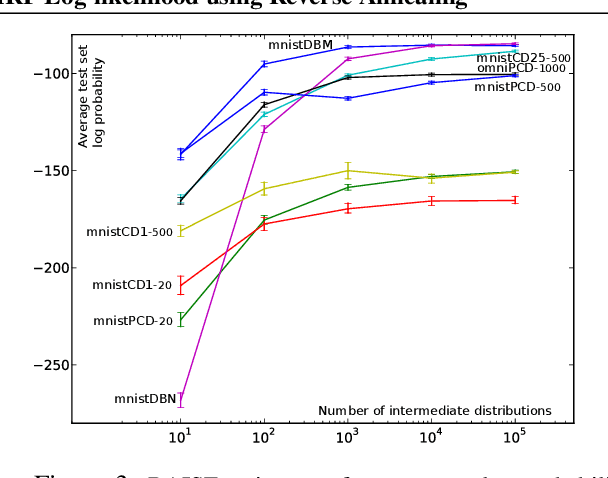
Markov random fields (MRFs) are difficult to evaluate as generative models because computing the test log-probabilities requires the intractable partition function. Annealed importance sampling (AIS) is widely used to estimate MRF partition functions, and often yields quite accurate results. However, AIS is prone to overestimate the log-likelihood with little indication that anything is wrong. We present the Reverse AIS Estimator (RAISE), a stochastic lower bound on the log-likelihood of an approximation to the original MRF model. RAISE requires only the same MCMC transition operators as standard AIS. Experimental results indicate that RAISE agrees closely with AIS log-probability estimates for RBMs, DBMs, and DBNs, but typically errs on the side of underestimating, rather than overestimating, the log-likelihood.

Testing MCMC code

Markov Chain Monte Carlo (MCMC) algorithms are a workhorse of probabilistic modeling and inference, but are difficult to debug, and are prone to silent failure if implemented naively. We outline several strategies for testing the correctness of MCMC algorithms. Specifically, we advocate writing code in a modular way, where conditional probability calculations are kept separate from the logic of the sampler. We discuss strategies for both unit testing and integration testing. As a running example, we show how a Python implementation of Gibbs sampling for a mixture of Gaussians model can be tested.