Accelerating Neural Network Training: An Analysis of the AlgoPerf Competition

The goal of the AlgoPerf: Training Algorithms competition is to evaluate practical speed-ups in neural network training achieved solely by improving the underlying training algorithms. In the external tuning ruleset, submissions must provide workload-agnostic hyperparameter search spaces, while in the self-tuning ruleset they must be completely hyperparameter-free. In both rulesets, submissions are compared on time-to-result across multiple deep learning workloads, training on fixed hardware. This paper presents the inaugural AlgoPerf competition's results, which drew 18 diverse submissions from 10 teams. Our investigation reveals several key findings: (1) The winning submission in the external tuning ruleset, using Distributed Shampoo, demonstrates the effectiveness of non-diagonal preconditioning over popular methods like Adam, even when compared on wall-clock runtime. (2) The winning submission in the self-tuning ruleset, based on the Schedule Free AdamW algorithm, demonstrates a new level of effectiveness for completely hyperparameter-free training algorithms. (3) The top-scoring submissions were surprisingly robust to workload changes. We also discuss the engineering challenges encountered in ensuring a fair comparison between different training algorithms. These results highlight both the significant progress so far, and the considerable room for further improvements.

Spectral-factorized Positive-definite Curvature Learning for NN Training

Many training methods, such as Adam(W) and Shampoo, learn a positive-definite curvature matrix and apply an inverse root before preconditioning. Recently, non-diagonal training methods, such as Shampoo, have gained significant attention; however, they remain computationally inefficient and are limited to specific types of curvature information due to the costly matrix root computation via matrix decomposition. To address this, we propose a Riemannian optimization approach that dynamically adapts spectral-factorized positive-definite curvature estimates, enabling the efficient application of arbitrary matrix roots and generic curvature learning. We demonstrate the efficacy and versatility of our approach in positive-definite matrix optimization and covariance adaptation for gradient-free optimization, as well as its efficiency in curvature learning for neural net training.

Position: Curvature Matrices Should Be Democratized via Linear Operators

Structured large matrices are prevalent in machine learning. A particularly important class is curvature matrices like the Hessian, which are central to understanding the loss landscape of neural nets (NNs), and enable second-order optimization, uncertainty quantification, model pruning, data attribution, and more. However, curvature computations can be challenging due to the complexity of automatic differentiation, and the variety and structural assumptions of curvature proxies, like sparsity and Kronecker factorization. In this position paper, we argue that linear operators -- an interface for performing matrix-vector products -- provide a general, scalable, and user-friendly abstraction to handle curvature matrices. To support this position, we developed $\textit{curvlinops}$, a library that provides curvature matrices through a unified linear operator interface. We demonstrate with $\textit{curvlinops}$ how this interface can hide complexity, simplify applications, be extensible and interoperable with other libraries, and scale to large NNs.

Influence Functions for Scalable Data Attribution in Diffusion Models

Diffusion models have led to significant advancements in generative modelling. Yet their widespread adoption poses challenges regarding data attribution and interpretability. In this paper, we aim to help address such challenges in diffusion models by developing an \textit{influence functions} framework. Influence function-based data attribution methods approximate how a model's output would have changed if some training data were removed. In supervised learning, this is usually used for predicting how the loss on a particular example would change. For diffusion models, we focus on predicting the change in the probability of generating a particular example via several proxy measurements. We show how to formulate influence functions for such quantities and how previously proposed methods can be interpreted as particular design choices in our framework. To ensure scalability of the Hessian computations in influence functions, we systematically develop K-FAC approximations based on generalised Gauss-Newton matrices specifically tailored to diffusion models. We recast previously proposed methods as specific design choices in our framework and show that our recommended method outperforms previous data attribution approaches on common evaluations, such as the Linear Data-modelling Score (LDS) or retraining without top influences, without the need for method-specific hyperparameter tuning.

Can We Remove the Square-Root in Adaptive Gradient Methods? A Second-Order Perspective

Adaptive gradient optimizers like Adam(W) are the default training algorithms for many deep learning architectures, such as transformers. Their diagonal preconditioner is based on the gradient outer product which is incorporated into the parameter update via a square root. While these methods are often motivated as approximate second-order methods, the square root represents a fundamental difference. In this work, we investigate how the behavior of adaptive methods changes when we remove the root, i.e. strengthen their second-order motivation. Surprisingly, we find that such square-root-free adaptive methods close the generalization gap to SGD on convolutional architectures, while maintaining their root-based counterpart's performance on transformers. The second-order perspective also has practical benefits for the development of adaptive methods with non-diagonal preconditioner. In contrast to root-based counterparts like Shampoo, they do not require numerically unstable matrix square roots and therefore work well in low precision, which we demonstrate empirically. This raises important questions regarding the currently overlooked role of adaptivity for the success of adaptive methods since the success is often attributed to sign descent induced by the root.

Structured Inverse-Free Natural Gradient: Memory-Efficient & Numerically-Stable KFAC for Large Neural Nets

Second-order methods for deep learning -- such as KFAC -- can be useful for neural net training. However, they are often memory-inefficient and numerically unstable for low-precision training since their preconditioning Kronecker factors are dense, and require high-precision matrix inversion or decomposition. Consequently, such methods are not widely used for training large neural networks such as transformer-based models. We address these two issues by (i) formulating an inverse-free update of KFAC and (ii) imposing structures in each of the Kronecker factors, resulting in a method we term structured inverse-free natural gradient descent (SINGD). On large modern neural networks, we show that, in contrast to KFAC, SINGD is memory efficient and numerically robust, and often outperforms AdamW even in half precision. Hence, our work closes a gap between first-order and second-order methods in modern low precision training for large neural nets.

Kronecker-Factored Approximate Curvature for Modern Neural Network Architectures

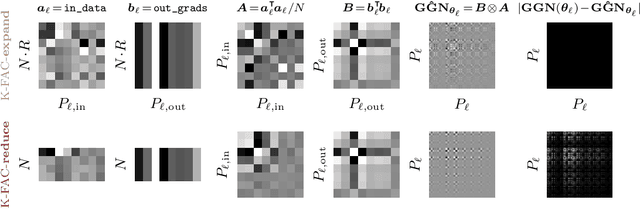
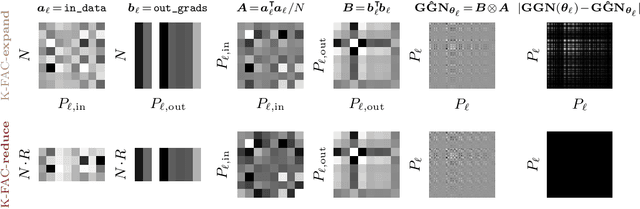
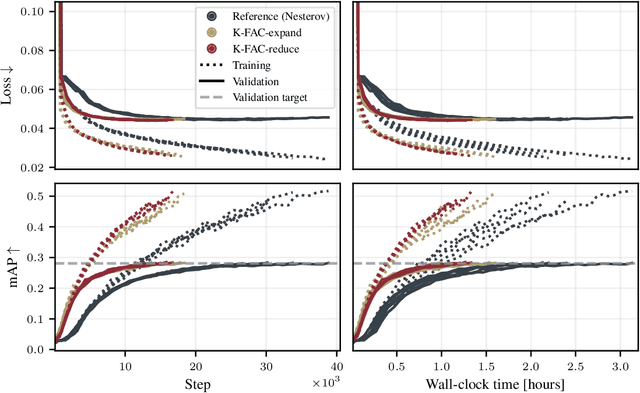
The core components of many modern neural network architectures, such as transformers, convolutional, or graph neural networks, can be expressed as linear layers with $\textit{weight-sharing}$. Kronecker-Factored Approximate Curvature (K-FAC), a second-order optimisation method, has shown promise to speed up neural network training and thereby reduce computational costs. However, there is currently no framework to apply it to generic architectures, specifically ones with linear weight-sharing layers. In this work, we identify two different settings of linear weight-sharing layers which motivate two flavours of K-FAC -- $\textit{expand}$ and $\textit{reduce}$. We show that they are exact for deep linear networks with weight-sharing in their respective setting. Notably, K-FAC-reduce is generally faster than K-FAC-expand, which we leverage to speed up automatic hyperparameter selection via optimising the marginal likelihood for a Wide ResNet. Finally, we observe little difference between these two K-FAC variations when using them to train both a graph neural network and a vision transformer. However, both variations are able to reach a fixed validation metric target in $50$-$75\%$ of the number of steps of a first-order reference run, which translates into a comparable improvement in wall-clock time. This highlights the potential of applying K-FAC to modern neural network architectures.

Benchmarking Neural Network Training Algorithms

Training algorithms, broadly construed, are an essential part of every deep learning pipeline. Training algorithm improvements that speed up training across a wide variety of workloads (e.g., better update rules, tuning protocols, learning rate schedules, or data selection schemes) could save time, save computational resources, and lead to better, more accurate, models. Unfortunately, as a community, we are currently unable to reliably identify training algorithm improvements, or even determine the state-of-the-art training algorithm. In this work, using concrete experiments, we argue that real progress in speeding up training requires new benchmarks that resolve three basic challenges faced by empirical comparisons of training algorithms: (1) how to decide when training is complete and precisely measure training time, (2) how to handle the sensitivity of measurements to exact workload details, and (3) how to fairly compare algorithms that require hyperparameter tuning. In order to address these challenges, we introduce a new, competitive, time-to-result benchmark using multiple workloads running on fixed hardware, the AlgoPerf: Training Algorithms benchmark. Our benchmark includes a set of workload variants that make it possible to detect benchmark submissions that are more robust to workload changes than current widely-used methods. Finally, we evaluate baseline submissions constructed using various optimizers that represent current practice, as well as other optimizers that have recently received attention in the literature. These baseline results collectively demonstrate the feasibility of our benchmark, show that non-trivial gaps between methods exist, and set a provisional state-of-the-art for future benchmark submissions to try and surpass.

Promises and Pitfalls of the Linearized Laplace in Bayesian Optimization

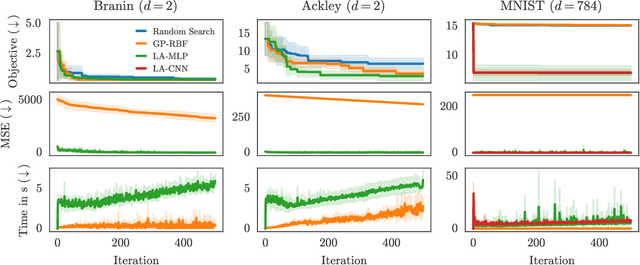
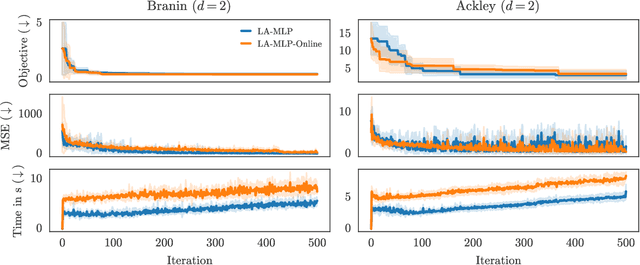
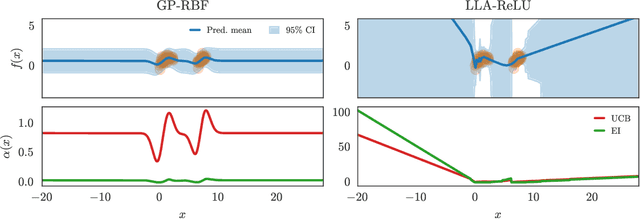
The linearized-Laplace approximation (LLA) has been shown to be effective and efficient in constructing Bayesian neural networks. It is theoretically compelling since it can be seen as a Gaussian process posterior with the mean function given by the neural network's maximum-a-posteriori predictive function and the covariance function induced by the empirical neural tangent kernel. However, while its efficacy has been studied in large-scale tasks like image classification, it has not been studied in sequential decision-making problems like Bayesian optimization where Gaussian processes -- with simple mean functions and kernels such as the radial basis function -- are the de-facto surrogate models. In this work, we study the usefulness of the LLA in Bayesian optimization and highlight its strong performance and flexibility. However, we also present some pitfalls that might arise and a potential problem with the LLA when the search space is unbounded.

Approximate Bayesian Neural Operators: Uncertainty Quantification for Parametric PDEs

Neural operators are a type of deep architecture that learns to solve (i.e. learns the nonlinear solution operator of) partial differential equations (PDEs). The current state of the art for these models does not provide explicit uncertainty quantification. This is arguably even more of a problem for this kind of tasks than elsewhere in machine learning, because the dynamical systems typically described by PDEs often exhibit subtle, multiscale structure that makes errors hard to spot by humans. In this work, we first provide a mathematically detailed Bayesian formulation of the ''shallow'' (linear) version of neural operators in the formalism of Gaussian processes. We then extend this analytic treatment to general deep neural operators using approximate methods from Bayesian deep learning. We extend previous results on neural operators by providing them with uncertainty quantification. As a result, our approach is able to identify cases, and provide structured uncertainty estimates, where the neural operator fails to predict well.