Richard Turner
Early predicting of hospital admission using machine learning algorithms: Priority queues approach
Jan 21, 2026Abstract:Emergency Department overcrowding is a critical issue that compromises patient safety and operational efficiency, necessitating accurate demand forecasting for effective resource allocation. This study evaluates and compares three distinct predictive models: Seasonal AutoRegressive Integrated Moving Average with eXogenous regressors (SARIMAX), EXtreme Gradient Boosting (XGBoost) and Long Short-Term Memory (LSTM) networks for forecasting daily ED arrivals over a seven-day horizon. Utilizing data from an Australian tertiary referral hospital spanning January 2017 to December 2021, this research distinguishes itself by decomposing demand into eight specific ward categories and stratifying patients by clinical complexity. To address data distortions caused by the COVID-19 pandemic, the study employs the Prophet model to generate synthetic counterfactual values for the anomalous period. Experimental results demonstrate that all three proposed models consistently outperform a seasonal naive baseline. XGBoost demonstrated the highest accuracy for predicting total daily admissions with a Mean Absolute Error of 6.63, while the statistical SARIMAX model proved marginally superior for forecasting major complexity cases with an MAE of 3.77. The study concludes that while these techniques successfully reproduce regular day-to-day patterns, they share a common limitation in underestimating sudden, infrequent surges in patient volume.
A Fourier Space Perspective on Diffusion Models
May 16, 2025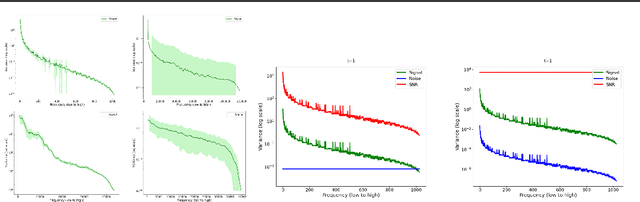

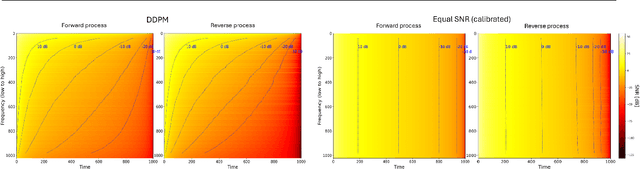
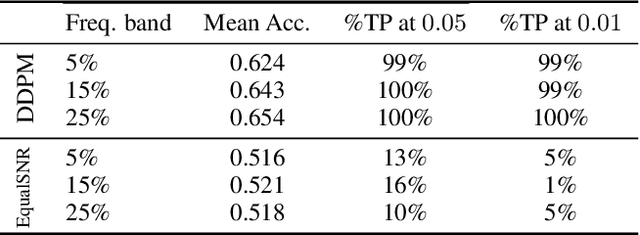
Abstract:Diffusion models are state-of-the-art generative models on data modalities such as images, audio, proteins and materials. These modalities share the property of exponentially decaying variance and magnitude in the Fourier domain. Under the standard Denoising Diffusion Probabilistic Models (DDPM) forward process of additive white noise, this property results in high-frequency components being corrupted faster and earlier in terms of their Signal-to-Noise Ratio (SNR) than low-frequency ones. The reverse process then generates low-frequency information before high-frequency details. In this work, we study the inductive bias of the forward process of diffusion models in Fourier space. We theoretically analyse and empirically demonstrate that the faster noising of high-frequency components in DDPM results in violations of the normality assumption in the reverse process. Our experiments show that this leads to degraded generation quality of high-frequency components. We then study an alternate forward process in Fourier space which corrupts all frequencies at the same rate, removing the typical frequency hierarchy during generation, and demonstrate marked performance improvements on datasets where high frequencies are primary, while performing on par with DDPM on standard imaging benchmarks.
Influence Functions for Scalable Data Attribution in Diffusion Models
Oct 17, 2024Abstract:Diffusion models have led to significant advancements in generative modelling. Yet their widespread adoption poses challenges regarding data attribution and interpretability. In this paper, we aim to help address such challenges in diffusion models by developing an \textit{influence functions} framework. Influence function-based data attribution methods approximate how a model's output would have changed if some training data were removed. In supervised learning, this is usually used for predicting how the loss on a particular example would change. For diffusion models, we focus on predicting the change in the probability of generating a particular example via several proxy measurements. We show how to formulate influence functions for such quantities and how previously proposed methods can be interpreted as particular design choices in our framework. To ensure scalability of the Hessian computations in influence functions, we systematically develop K-FAC approximations based on generalised Gauss-Newton matrices specifically tailored to diffusion models. We recast previously proposed methods as specific design choices in our framework and show that our recommended method outperforms previous data attribution approaches on common evaluations, such as the Linear Data-modelling Score (LDS) or retraining without top influences, without the need for method-specific hyperparameter tuning.
Challenges and Pitfalls of Bayesian Unlearning
Jul 07, 2022
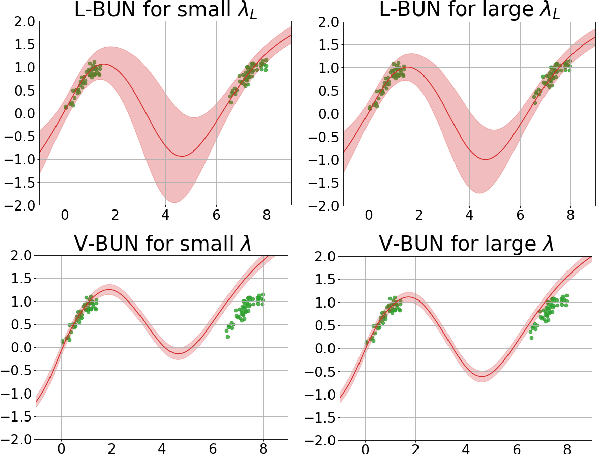
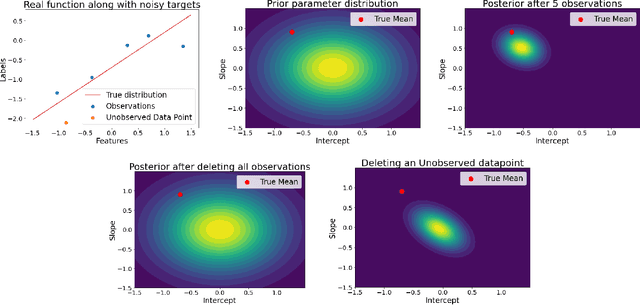
Abstract:Machine unlearning refers to the task of removing a subset of training data, thereby removing its contributions to a trained model. Approximate unlearning are one class of methods for this task which avoid the need to retrain the model from scratch on the retained data. Bayes' rule can be used to cast approximate unlearning as an inference problem where the objective is to obtain the updated posterior by dividing out the likelihood of deleted data. However this has its own set of challenges as one often doesn't have access to the exact posterior of the model parameters. In this work we examine the use of the Laplace approximation and Variational Inference to obtain the updated posterior. With a neural network trained for a regression task as the guiding example, we draw insights on the applicability of Bayesian unlearning in practical scenarios.
Efficient Gaussian Neural Processes for Regression
Aug 24, 2021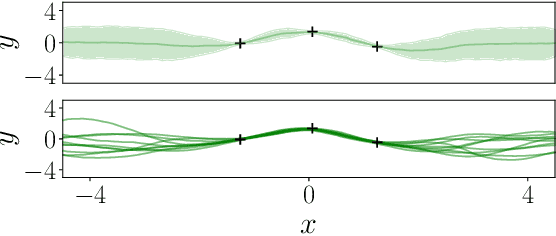
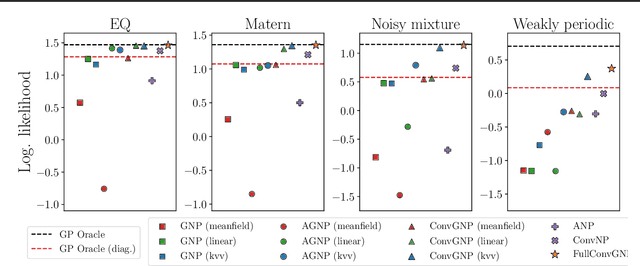
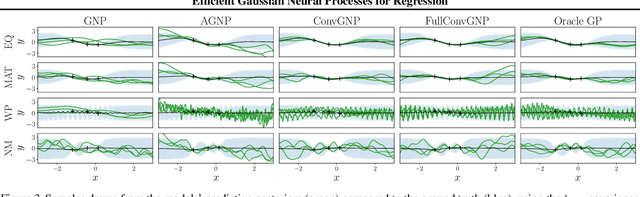
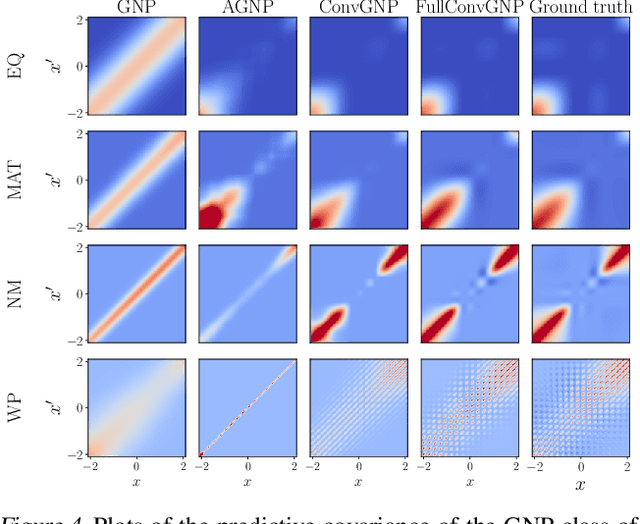
Abstract:Conditional Neural Processes (CNP; Garnelo et al., 2018) are an attractive family of meta-learning models which produce well-calibrated predictions, enable fast inference at test time, and are trainable via a simple maximum likelihood procedure. A limitation of CNPs is their inability to model dependencies in the outputs. This significantly hurts predictive performance and renders it impossible to draw coherent function samples, which limits the applicability of CNPs in down-stream applications and decision making. Neural Processes (NPs; Garnelo et al., 2018) attempt to alleviate this issue by using latent variables, relying on these to model output dependencies, but introduces difficulties stemming from approximate inference. One recent alternative (Bruinsma et al.,2021), which we refer to as the FullConvGNP, models dependencies in the predictions while still being trainable via exact maximum-likelihood. Unfortunately, the FullConvGNP relies on expensive 2D-dimensional convolutions, which limit its applicability to only one-dimensional data. In this work, we present an alternative way to model output dependencies which also lends itself maximum likelihood training but, unlike the FullConvGNP, can be scaled to two- and three-dimensional data. The proposed models exhibit good performance in synthetic experiments.
Bayesian Neural Network Priors Revisited
Feb 12, 2021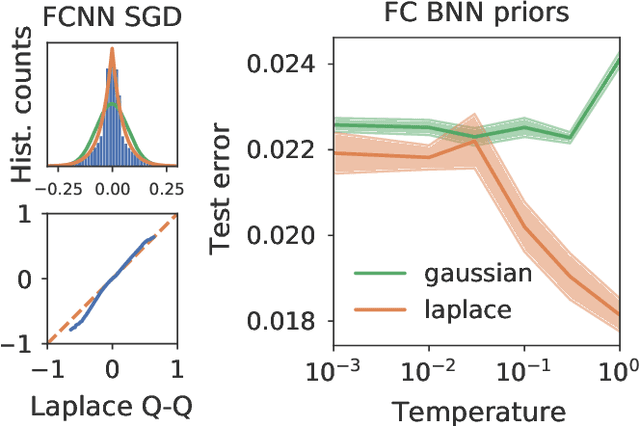
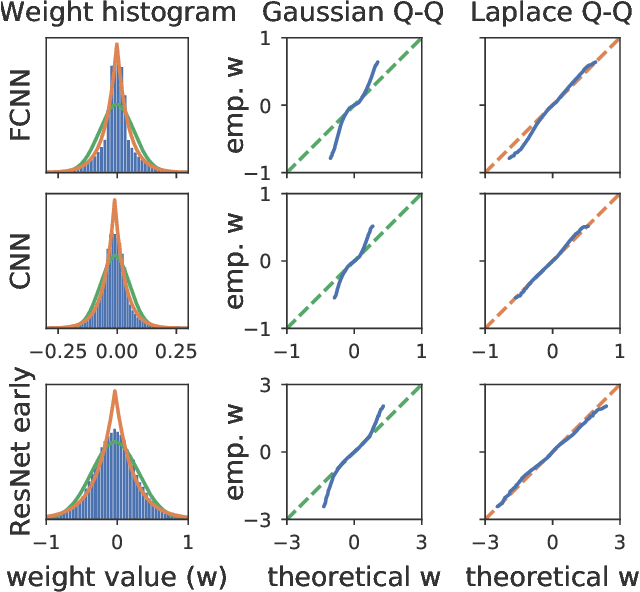
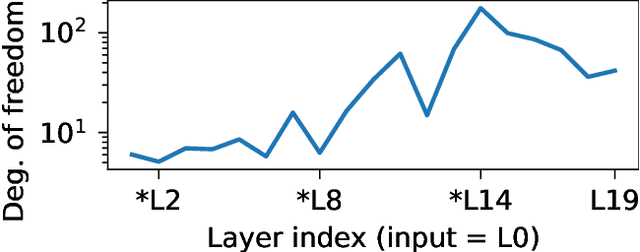
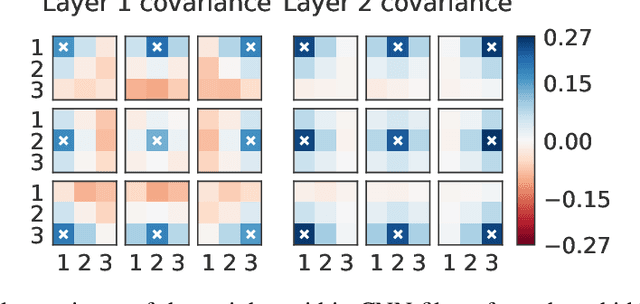
Abstract:Isotropic Gaussian priors are the de facto standard for modern Bayesian neural network inference. However, such simplistic priors are unlikely to either accurately reflect our true beliefs about the weight distributions, or to give optimal performance. We study summary statistics of neural network weights in different networks trained using SGD. We find that fully connected networks (FCNNs) display heavy-tailed weight distributions, while convolutional neural network (CNN) weights display strong spatial correlations. Building these observations into the respective priors leads to improved performance on a variety of image classification datasets. Moreover, we find that these priors also mitigate the cold posterior effect in FCNNs, while in CNNs we see strong improvements at all temperatures, and hence no reduction in the cold posterior effect.
VAEM: a Deep Generative Model for Heterogeneous Mixed Type Data
Jun 21, 2020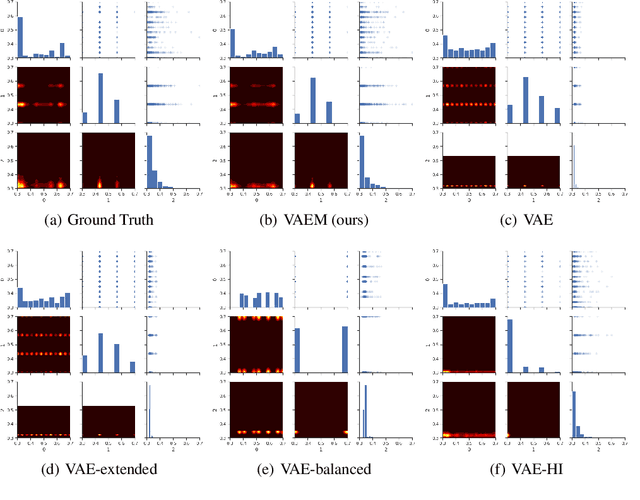

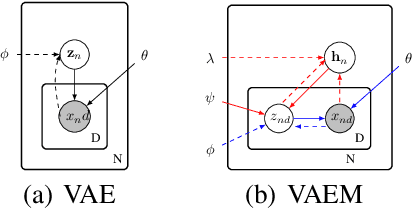
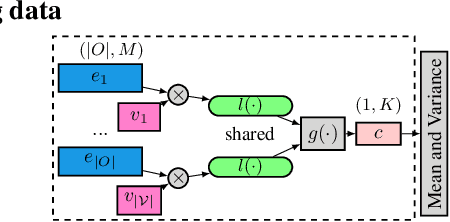
Abstract:Deep generative models often perform poorly in real-world applications due to the heterogeneity of natural data sets. Heterogeneity arises from data containing different types of features (categorical, ordinal, continuous, etc.) and features of the same type having different marginal distributions. We propose an extension of variational autoencoders (VAEs) called VAEM to handle such heterogeneous data. VAEM is a deep generative model that is trained in a two stage manner such that the first stage provides a more uniform representation of the data to the second stage, thereby sidestepping the problems caused by heterogeneous data. We provide extensions of VAEM to handle partially observed data, and demonstrate its performance in data generation, missing data prediction and sequential feature selection tasks. Our results show that VAEM broadens the range of real-world applications where deep generative models can be successfully deployed.
Icebreaker: Element-wise Active Information Acquisition with Bayesian Deep Latent Gaussian Model
Aug 14, 2019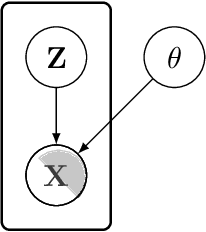
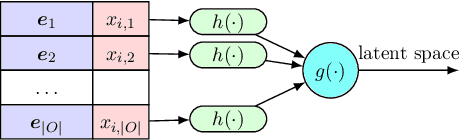
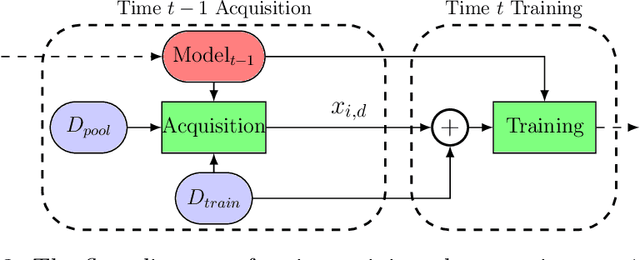
Abstract:In this paper we introduce the ice-start problem, i.e., the challenge of deploying machine learning models when only little or no training data is initially available, and acquiring each feature element of data is associated with costs. This setting is representative for the real-world machine learning applications. For instance, in the health-care domain, when training an AI system for predicting patient metrics from lab tests, obtaining every single measurement comes with a high cost. Active learning, where only the label is associated with a cost does not apply to such problem, because performing all possible lab tests to acquire a new training datum would be costly, as well as unnecessary due to redundancy. We propose Icebreaker, a principled framework to approach the ice-start problem. Icebreaker uses a full Bayesian Deep Latent Gaussian Model (BELGAM) with a novel inference method. Our proposed method combines recent advances in amortized inference and stochastic gradient MCMC to enable fast and accurate posterior inference. By utilizing BELGAM's ability to fully quantify model uncertainty, we also propose two information acquisition functions for imputation and active prediction problems. We demonstrate that BELGAM performs significantly better than the previous VAE (Variational autoencoder) based models, when the data set size is small, using both machine learning benchmarks and real-world recommender systems and health-care applications. Moreover, based on BELGAM, Icebreaker further improves the performance and demonstrate the ability to use minimum amount of the training data to obtain the highest test time performance.
Invariant Models for Causal Transfer Learning
Sep 24, 2018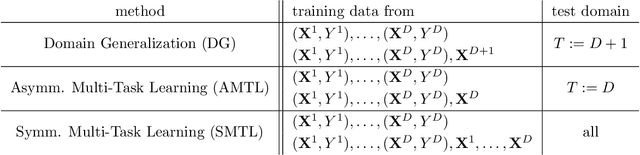
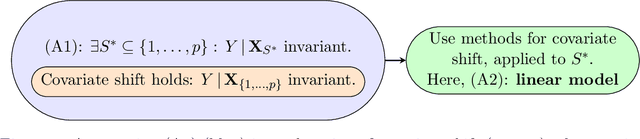
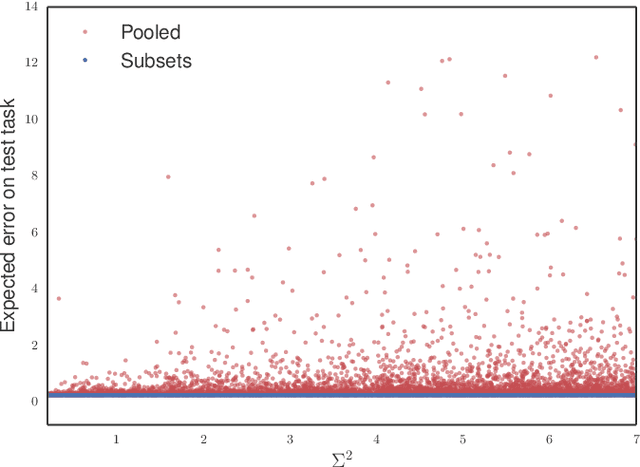

Abstract:Methods of transfer learning try to combine knowledge from several related tasks (or domains) to improve performance on a test task. Inspired by causal methodology, we relax the usual covariate shift assumption and assume that it holds true for a subset of predictor variables: the conditional distribution of the target variable given this subset of predictors is invariant over all tasks. We show how this assumption can be motivated from ideas in the field of causality. We focus on the problem of Domain Generalization, in which no examples from the test task are observed. We prove that in an adversarial setting using this subset for prediction is optimal in Domain Generalization; we further provide examples, in which the tasks are sufficiently diverse and the estimator therefore outperforms pooling the data, even on average. If examples from the test task are available, we also provide a method to transfer knowledge from the training tasks and exploit all available features for prediction. However, we provide no guarantees for this method. We introduce a practical method which allows for automatic inference of the above subset and provide corresponding code. We present results on synthetic data sets and a gene deletion data set.
Overpruning in Variational Bayesian Neural Networks
Jan 18, 2018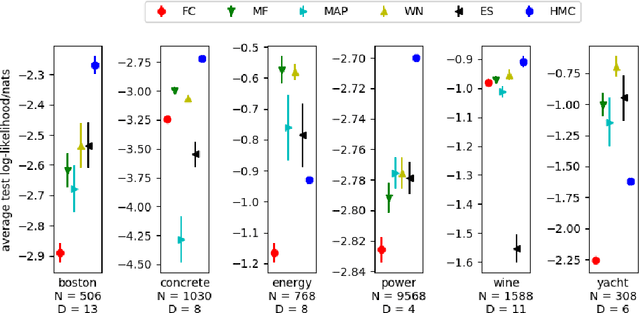
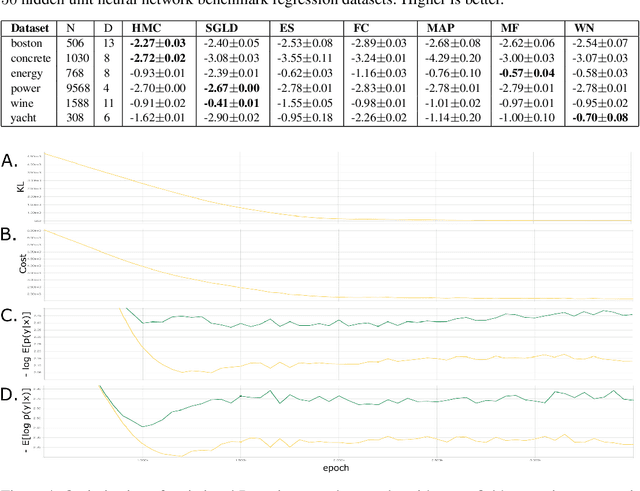
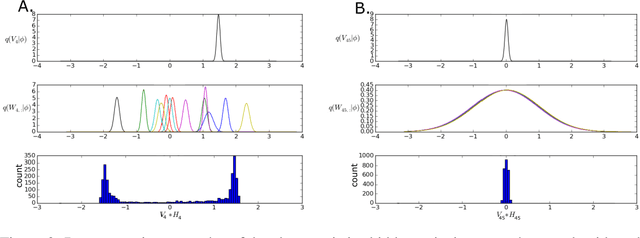
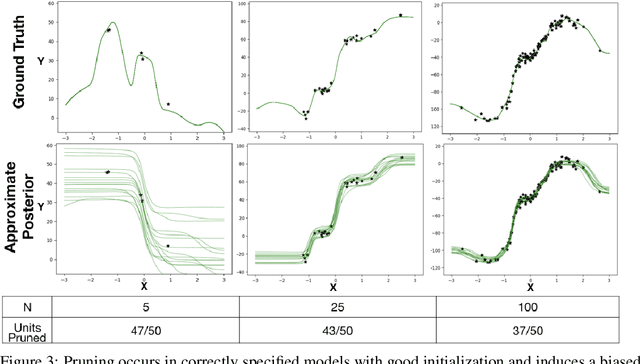
Abstract:The motivations for using variational inference (VI) in neural networks differ significantly from those in latent variable models. This has a counter-intuitive consequence; more expressive variational approximations can provide significantly worse predictions as compared to those with less expressive families. In this work we make two contributions. First, we identify a cause of this performance gap, variational over-pruning. Second, we introduce a theoretically grounded explanation for this phenomenon. Our perspective sheds light on several related published results and provides intuition into the design of effective variational approximations of neural networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge